* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Sec. 8 – 2 Similar Polygons
List of regular polytopes and compounds wikipedia , lookup
Multilateration wikipedia , lookup
Tessellation wikipedia , lookup
Rational trigonometry wikipedia , lookup
Renormalization group wikipedia , lookup
History of trigonometry wikipedia , lookup
Trigonometric functions wikipedia , lookup
List of works designed with the golden ratio wikipedia , lookup
Euler angles wikipedia , lookup
Golden ratio wikipedia , lookup
Euclidean geometry wikipedia , lookup
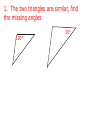
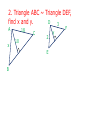
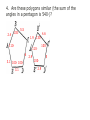
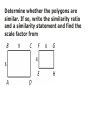
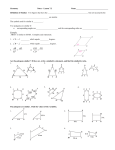
Sec. 6–2 Similar Polygons Figures that are similar (~) have the same shape but not necessarily the same size. Angles are congruent, Sides are proportional If two figures are similar, not only are their sides proportional, all their linear parts are proportional (such as the height, median, midsegment, diagonals, etc). Writing a similarity statement is like writing a congruence statement—be sure to list corresponding vertices in the same order. Scale Factor: If two polygons are similar, then the ratio of the lengths of two corresponding sides is called the scale factor. 1. The two triangles are similar, find the missing angles 50° 120° 2. Triangle ABC ~ Triangle DEF, find x and y. D 3 A x 18 10 C 2 E B y F 3. Two similar rectangles have sides in the ratio of 3 : 7. If the smaller rectangle has a perimeter of 50m, find the perimeter of the larger rectangle. 4. Are these polygons similar (the sum of the angles in a pentagon is 540◦)? 2.4 130◦ 5.5 1.9 110◦ 130◦ 100◦ 110◦ 6 3.1 100◦ 100◦ 3.1 2.9 4.6 100◦ 2.9 5 Determine whether the polygons are similar. If so, write the similarity ratio and a similarity statement and find the scale factor from quad ABCD to quad EFGH.