Download Geometric Mean PowerPoint

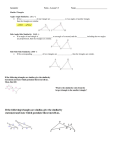
8-1 Similarity in Right Triangles
Objectives
Use geometric mean to find segment
lengths in right triangles.
Apply similarity relationships in right
triangles to solve problems.
Holt Geometry
8-1 Similarity in Right Triangles
Vocabulary
geometric mean
Holt Geometry
8-1 Similarity in Right Triangles
The geometric mean of two positive numbers is the
positive square root of their product.
Consider the proportion
. In this case, the
means of the proportion are the same number, and
that number (x) is the geometric mean of the extremes.
Holt Geometry
8-1 Similarity in Right Triangles
Example 1A: Finding Geometric Means
Find the geometric mean of each pair of
numbers. If necessary, give the answer in
simplest radical form.
4 and 9
Let x be the geometric mean.
4 x

x 9
x 2  36
x=6
Holt Geometry
Def. of geometric mean
Cross multiply
Find the positive square root.
8-1 Similarity in Right Triangles
Example 1b: Finding Geometric Means
Find the geometric mean of each pair of
numbers. If necessary, give the answer in
simplest radical form.
6 and 15
Let x be the geometric mean.
6 x

x 15
x 2  90
x  3 10
Holt Geometry
Def. of geometric mean
Cross multiply
Find the positive square root.
8-1 Similarity in Right Triangles
Example 1c: Finding Geometric Means
Find the geometric mean of each pair of
numbers. If necessary, give the answer in
simplest radical form.
2 and 8
Let x be the geometric mean.
2 x

x 8
x 2  16
x4
Holt Geometry
Def. of geometric mean
Cross multiply
Find the positive square root.
8-1 Similarity in Right Triangles
In a right triangle, an altitude drawn from the
vertex of the right angle to the hypotenuse forms
two right triangles.
Holt Geometry
8-1 Similarity in Right Triangles
Example: Identifying Similar Right Triangles
Write a similarity
statement comparing the
three triangles.
Sketch the three right triangles with the
angles of the triangles in corresponding
positions.
W
Z
By Theorem 8-1-1, ∆UVW ~ ∆UWZ ~ ∆WVZ.
Holt Geometry
8-1 Similarity in Right Triangles
Example 1
2 n = 10,
10 h = ___
m = 2,
h 10

2 h
2
h  20
h  20
h2 5
Holt Geometry
a
b
hh
m
n
c
8-1 Similarity in Right Triangles
Example 2
10 b = ___
m = 2,
2 n = 10,
a
b
hh
m
n
c
12
12 b

b 10
b 2  120
b  120
b  2 30
Holt Geometry
8-1 Similarity in Right Triangles
Example 2
n = 27
27, c = 30,
30 b = ___
a
b
hh
m
n
c
30 b

b 27
b 2  810
b  810
b  9 10
Holt Geometry
8-1 Similarity in Right Triangles
Helpful Hint
Once you’ve found the unknown side lengths,
you can use the Pythagorean Theorem to check
your answers.
Holt Geometry