Download lecture1-Science

CDT403 Research Methodology in Natural Sciences and Engineering
Theory of Science
INFORMATION, COMPUTATION,
KNOWLEDGE AND SCIENCE
Gordana Dodig-Crnkovic
School of Innovation, Design and Engineering
Mälardalen University
1
Science: Big Picture
Science and the Universe
The Mytho-Poetic Universe
The Medieval Divine Geocentric Universe
The Clockwork (Mechanistic) Universe
The Computational Universe
Info-Computationalism
Information
Computation
Natural computation – beyond Turing Model
Naturalist Understanding of Cognition
Info-Computational Knowlede Generation
Science, Knowledge, Truth and Meaning
Science
Scientific Method
Knowledge and its production
Justification and Truth
Proof and Axiomatic systems, Gödel theorems
Meaning
2
Science: Big Picture First
3
Science and the Universe
http://www.youtube.com/watch?v=i43bNclKQN0
MACROCOSMOS TO MICROCOSMOS.wmv
http://www.youtube.com/watch?v=akbilxS1dGc&feature=related Zoom
Out - Zoom In
Similar:
http://www.youtube.com/watch?v=dAzJy_DECyQ&feature=related
Cosmic Super Zoom
http://www.youtube.com/watch?v=Vs5doooe2VY&feature=related From
Milky Way to Quarks
4
The Mytho-Poetic Universe
In ancient Egypt the dome
of the sky was represented
by the goddess Nut, She
was the night sky, and the
sun, the god Ra, was born
from her every morning.
5
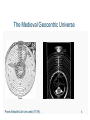
The Medieval Geocentric Universe
From Aristotle Libri de caelo (1519).
6
The Clockwork (Mechanistic) Universe
The mechanicistic paradigm which systematically revealed physical
structure in analogy with the artificial. The self-functioning automaton
- basis and canon of the form of the Universe.
Newton Philosophiae Naturalis Principia Matematica, 1687
7
The Computational Universe
We are all living inside a gigantic
computer. No, not The Matrix: the
Universe.
Every process, every change that
takes place in the Universe, may
be considered as a kind of
computation.
E Fredkin, S Wolfram, G Chaitin
The universe is on a fundamental level an
info-computational phenomenon. GDC
http://www.nature.com/nsu/020527/020527-16.html
8
The Computational Universe
Konrad Zuse was the first to suggest (in 1967) that the physical
behavior of the entire universe is being computed on a basic level,
possibly on cellular automata, by the universe itself which he
referred to as "Rechnender Raum" or Computing Space/Cosmos.
Computationalists: Zuse, Wiener, Fredkin, Wolfram, Chaitin, Lloyd,
Seife, 't Hooft, Deutsch, Tegmark, Schmidhuber, Weizsäcker,
Wheeler..
http://en.wikipedia.org/wiki/Pancomputationalism
9
Info-Computationalism
Information and computation are two interrelated and mutually
defining phenomena – there is no computation without information
(computation understood as information processing), and vice
versa, there is no information without computation (all information
is a result of computational processes).
Being interconnected, information is studied as a structure, while
computation presents a process on an informational structure. In
order to learn about foundations of information, we must also study
computation.
Information
A special issue of the
Journal of Logic, Language and Information (Volume 12 No 4 2003)
dedicated to the different facets of information.
A Handbook on the Philosophy of Information (Van Benthem,
Adriaans) is in preparation as one volume Handbook of the
philosophy of science. http://www.illc.uva.nl/HPI/
Computation
The Computing Universe: Pancomputationalism
Computation is generally defined as information processing.
(See Burgin, M., Super-Recursive Algorithms, Springer Monographs
in Computer Science, 2005)
For different views see e.g.
http://people.pwf.cam.ac.uk/mds26/cogsci/program.html Computation
and Cognitive Science 7–8 July 2008, King's College Cambridge
The definition of computation is widely debated, and an entire issue of the
journal Minds and Machines (1994, 4, 4) was devoted to the question
“What is Computation?” Even: Theoretical Computer Science 317 (2004)
Present Model of Computation: Turing Machine
......
......
Tape
Control Unit
Read-Write head
1. Reads a symbol
2. Writes a symbol
3. Moves Left or Right
http://plato.stanford.edu/entries/turing-machine/
Computing Nature and
Nature Inspired Computation
Natural computation includes
computation that occurs in nature or is
inspired by nature. Computing
Inspired by nature:
•Evolutionary computation
•Neural networks
•Artificial immune systems
•Swarm intelligence
In 1623, Galileo in his book The Assayer - Il Saggiatore,
claimed that the language of nature's book is
mathematics and that the way to understand nature is
through mathematics. Generalizing ”mathematics” to
”computation” we may agree with Galileo – the great
book of nature is an e-book!
Simulation and emulation of nature:
•Fractal geometry
•Artificial life
Computing with natural materials:
•DNA computing
•Quantum computing
Journals: Natural Computing and IEEE Transactions on Evolutionary Computation.
Turing Machines Limitations –
Self-Generating Living Systems
Complex biological systems must be modeled as
self-referential, self-organizing "componentsystems" (George Kampis) which are selfgenerating and whose behavior, though
computational in a general sense, goes far
beyond Turing machine model.
“a component system is a computer which, when executing its operations
(software) builds a new hardware.... [W]e have a computer that re-wires itself in a
hardware-software interplay: the hardware defines the software and the software
defines new hardware. Then the circle starts again.”
(Kampis, p. 223 Self-Modifying Systems in Biology and Cognitive Science)
Beyond Turing Machines
Ever since Turing proposed his machine model which identifies
computation with the execution of an algorithm, there have been
questions about how widely the Turing Machine (TM) model is
applicable.
With the advent of computer networks, which are the main paradigm
of computing today, the model of a computer in isolation, represented
by a Universal Turing Machine, has become insufficient.
The basic difference between an isolated computing box and a
network of computational processes (nature itself understood as a
computational mechanism) is the interactivity of computation. The
most general computational paradigm today is interactive computing
(Wegner, Goldin).
Beyond Turing Machines
The challenge to deal with computability in the real world (such
as computing on continuous data, biological computing/organic
computing, quantum computing, or generally natural computing)
has brought new understanding of computation.
Natural computing has different criteria for success of a
computation, halting problem is not a central issue, but instead
the adequacy of the computational response in a network of
interacting computational processes/devices. In many areas, we
have to computationally model emergence not being clearly
algorithmic. (Barry Cooper)
Correspondence Principle
picture after Stuart A. Umpleby
http://www.gwu.edu/~umpleby/recent_papers/2004_what_i_learned_from_heinz_vo
n_foerster_figures_by_umpleby.htm
Natural Computation
TM
Info-Computationalism Applied:
Naturalizing Epistemology
Naturalized epistemology (Feldman, Kornblith, Stich) is, in general, an
idea that knowledge may be studied as a natural phenomenon -that the subject matter of epistemology is not our concept of
knowledge, but the knowledge itself.
“The stimulation of his sensory receptors is all the evidence anybody
has had to go on, ultimately, in arriving at his picture of the world. Why
not just see how this construction really proceeds? Why not settle
for psychology? “("Epistemology Naturalized", Quine 1969; emphasis
mine)
I will re-phrase the question to be: Why not settle for computing?
Epistemology is the branch of philosophy that studies the nature, methods, limitations,
and validity of knowledge and belief.
Naturalist Understanding of Cognition
According to Maturana and Varela (1980) even the simplest
organisms possess cognition and their meaning-production
apparatus is contained in their metabolism. Of course, there are
also non-metabolic interactions with the environment, such as
locomotion, that also generates meaning for an organism by
changing its environment and providing new input data.
Maturana’s and Varelas’ understanding that all living organisms
posess some cognition, in some degree. is most suitable as the
basis for a computationalist account of the naturalized
evolutionary epistemology.
Info-Computational Account of
Knowledge Generation
Natural computing as a new paradigm of computing
goes beyond the Turing Machine model and applies
to all physical processes including those going on in
our brains.
The next great change in computer science and
information technology will come from mimicking the
techniques by which biological organisms process
information.
To do this computer scientists must draw on
expertise in subjects not usually associated with
their field, including organic chemistry, molecular
biology, bioengineering, and smart materials.
Info-Computational Account of
Knowledge Generation
At the physical level, living beings are open complex
computational systems in a regime on the edge of chaos,
characterized by maximal informational content. Complexity is
found between orderly systems with high information
compressibility and low information content and random systems
with low compressibility and high information content. (Flake)
The essential feature of cognizing living organisms is their ability
to manage complexity, and to handle complicated environmental
conditions with a variety of responses which are results of
adaptation, variation, selection, learning, and/or reasoning. (GellMann)
Cognition as Restructuring of an Agent in
Interaction with the Environment
As a result of evolution, increasingly complex living organisms arise
that are able to survive and adapt to their environment. It means they
are able to register inputs (data) from the environment, to structure
those into information, and in more developed organisms into
knowledge. The evolutionary advantage of using structured,
component-based approaches is improving response-time and
efficiency of cognitive processes of an organism.
The Dual network model, suggested by Goertzel for modeling
cognition in a living organism describes mind in terms of two
superposed networks: a self-organizing associative memory network,
and a perceptual-motor process hierarchy, with the multi-level logic of
a flexible command structure.
Cognition as Restructuring of an Agent in
Interaction with the Environment
Naturalized knowledge generation acknowledges the body as our
basic cognitive instrument. All cognition is embodied cognition, in both
microorganisms and humans (Gärdenfors, Stuart). In more complex
cognitive agents, knowledge is built upon not only reasoning about
input information, but also on intentional choices, dependent on value
systems stored and organized in agents memory.
It is not surprising that present day interest in knowledge generation
places information and computation (communication) in focus, as
information and its processing are essential structural and dynamic
elements which characterize structuring of input data (data 
information  knowledge) by an interactive computational process
going on in the agent during the adaptive interplay with the
environment.
Natural Computing in Living Agents
- Agent-centered (information and
computation is in the agent)
- Agent is a cognizing biological organism
or an intelligent machine or both
- Interaction with the physical world and
other agents is essential
- Kind of physicalism with information as a
stuff of the universe
- Agents are parts of different cognitive
communities
- Self-organization
- Circularity (recursiveness) is central for
biological organisms
http://www.conscious-robots.com
What is computation? How does nature
compute? Learning from Nature *
“It always bothers me that, according to the laws as we understand
them today, it takes a computing machine an infinite number of
logical operations to figure out what goes on in no matter how tiny a
region of space, and no matter how tiny a region of time …
So I have often made the hypothesis that ultimately physics will not
require a mathematical statement, that in the end the machinery will
be revealed, and the laws will turn out to be simple, like the chequer
board with all its apparent complexities.”
Richard Feynman “The Character of Physical Law”
* 2008 Midwest NKS Conference, Fri Oct 31 - Sun Nov 2, 2008
Indiana University — Bloomington, IN
Paradigm Shift
•
•
•
•
•
•
•
•
•
•
Information/Computation
Discrete/Continuum
Natural interactive computing beyond Turing limit
Complex dynamic systems
Emergency
Logic
Philosophy
Human-centric (agent-centric)
Circularity and self-reflection
Ethics returns to researchers agenda
Info-Computational Paradigm of
Knowledge
• Understanding of info-computational mechanisms and processes
and their relationship to life and knowledge
• Argument for evolution of biological life, cognition and intelligence
• Development of new unconventional computational methods
• Learning from nature about optimizing solutions with limited
resources (Organic Computing)
• Providing a unified platform (framework) for specialist sciences to
communicate and create holistic (multi-disciplinary/interdisciplinary/transdisciplinary) views
A mathematical analysis of the scientific
method, the axiomatic method, and
Darwin's theory of evolution
G. J. Chaitin, IBM Research
http://www.umcs.maine.edu/~chaitin/ufrj.html
http://www.cs.auckland.ac.nz/~chaitin/ufrj.html
29
Chaitin’s work on Epistemology, Information
Theory, and Metamathematics important for
understanding of Formal Systems and their
Relationship with Biology
http://www.umcs.maine.edu/~chaitin/ecap.pdf Epistemology
as Information Theory: From Leibniz to Ω
http://www.umcs.maine.edu/~chaitin/mjm.pdf The Halting Probability
Omega: Irreducible Complexity in Pure Mathematics
http://www.umcs.maine.edu/~chaitin/unm.html Randomness in Arithmetic
and the Decline & Fall of Reductionism in Pure Mathematics
http://www.umcs.maine.edu/~chaitin/hu.html The Search for the
Perfect Language
30
Despite the fact that there can be no TOE (Theory
Of Everything) for pure mathematics as Hilbert
hoped, mathematicians remain enamored with
formal proof.
See the special issue on formal proof of the AMS
Notices, December 2008 (From Chaitin’s lectures)
http://www.ams.org/notices/200811/index.html
David Malone, Dangerous Knowledge, BBC TV, 90
minutes, Google video vividly illustrates the search for
TOE in mathematics
http://video.google.com/videoplay?docid=-5122859998068380459#
31
http://www.umcs.maine.edu/~chaitin/jack.html
Mathematics, Biology and Metabiology
http://www.umcs.maine.edu/~chaitin/ev.html
Evolution of Mutating Software
http://www.umcs.maine.edu/~chaitin/mex.html
Speculations on biology, information and complexity
http://www.scottaaronson.com/writings/bignumbers.html
Who Can Name the Bigger Number?
32
Science, Knowledge, Truth and Meaning
Critical thinking
What is science?
What is scientific method?
What is knowledge?
Information and knowledge
Truth and meaning
Limits of formal systems
Science as learning process
Info-computational view of knowledge production
Complexity
33
Red Thread: Critical Thinking
“Reserve your right to think,
for even to think wrongly
is better than not to think at all.”
Hypatia, natural philosopher and mathematician
34
Haiku – Like Highlights
.遠山が目玉にうつるとんぼ哉
tôyama ga medama
ni utsuru tombo kana
the distant mountain
reflected in his eyes...
dragonfly
Kobayashi Issa (1763-1827)
(Haiku form: 5-7-5 syllables)
35
What is Science?
Eye
Maurits Cornelis Escher
We can see Science from different perspectives…36
Definitions by Goal (Result) and Process (1)
science from Latin scientia, scire to know;
1: a department of systematized knowledge as an
object of study
2: knowledge or a system of knowledge covering
general truths or the operation of general laws
especially as obtained and tested through scientific
method
37
Definitions by Goal (Result) and Process (2)
3: such knowledge or such a system of knowledge
concerned with the physical world and its phenomena
: natural science
4: a system or method reconciling practical ends with
scientific laws <engineering is both a science and an
art>
38
Science: Definitions by Contrast
To do science is to search for repeated patterns, not
simply to accumulate facts.
Robert H. MacArthur
Religion is a culture of faith; science is a culture of doubt.
Richard Feynman
39
Empirical approach.
What Sciences are there?
Dewey Decimal Classification®
http://www.geocities.com/Athens/Troy/8866/15urls.html
000 - & Psychology
200 - ReliComputers, Information & General Reference
100 - Philosophy gion
300 - Social sciences
400 - Language
500 - Science
600 - Technology
700 - Arts & Recreation
800 - Literature
900 - History & Geography
40
Dewey Decimal Classification®
500 – Science
510 Mathematics
520 Astronomy
530 Physics
540 Chemistry
550 Earth Sciences & Geology
560 Fossils & Prehistoric Life
570 Biology & Life Sciences
580 Plants (Botany)
590 Animals (Zoology)
41
Language Based Scheme
Classical Sciences in their Cultural Context –
Logic
&
Mathematics
1
Natural Sciences
(Physics,
Chemistry,
Biology, …)
2
Culture
(Religion, Art, …)
5
Social Sciences
(Economics, Sociology,
Anthropology, …)
3
The Humanities
(Philosophy, History,
Linguistics …)
4
42
Understanding what science is
by understanding what scientists do
"Scientists are people of very dissimilar temperaments doing
different things in very different ways.
Among scientists are collectors, classifiers and compulsive
tidiers-up; many are detectives by temperament and many are
explorers; some are artists and others artisans.
There are poet-scientists and philosopher-scientists and even a
few mystics."
Peter Medawar, Pluto's Republic
43
The Classical (Ideal) Model of Science
The Classical Model of Science is a system S of propositions and
concepts satisfying the following conditions:
• All propositions and all concepts (or terms) of S concern a
specific set of objects or are about a certain domain of being(s).
• There are in S a number of so-called fundamental concepts (or
terms).
• All other concepts (or terms) occurring in S are composed of (or
are definable from) these fundamental concepts (or terms).
44
The Classical (Ideal) Model of Science
• There are in S a number of so-called fundamental propositions.
• All other propositions of S follow from or are grounded in (or are
provable or demonstrable from) these fundamental propositions.
• All propositions of S are true.
• All propositions of S are universal and necessary in some sense
or another.
45
The Classical (Ideal) Model of Science
• All concepts or terms of S are adequately known. A nonfundamental concept is adequately known through its
composition (or definition).
• The Classical Model of Science is a reconstruction a posteriori
and sums up the historical philosopher’s ideal of scientific
explanation.
• The fundamental is that “All propositions and all concepts (or
terms) of S concern a specific set of objects or are about a
certain domain of being(s).”
Betti A & De Jong W. R., Guest Editors, The Classical Model of Science I: A MillenniaOld Model of Scientific Rationality, Forthcoming in Synthese, Special Issue
46
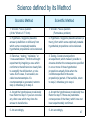
Science defined by its Method
Socratic Method
Scientific Method
1. Wonder. Pose a question
(of the “What is X ?” form).
1. Wonder. Pose a question.
(Formulate a problem).
2. Hypothesis. Suggest a plausible
answer (a definition or definiens) from
which some conceptually testable
hypothetical propositions can be deduced.
2. Hypothesis. Suggest a plausible answer (a
theory) from which some empirically testable
hypothetical propositions can be deduced.
3. Elenchus ; “testing,” “refutation,” or
“cross-examination.” Perform a thought
experiment by imagining a case which
conforms to the definiens but clearly fails
to exemplify the definiendum, or vice
versa. Such cases, if successful, are
called counterexamples. If a
counterexample is generated, return to
step 2, otherwise go to step 4.
3. Testing. Construct and perform
an experiment, which makes it possible to
observe whether the consequences specified
in one or more of those hypothetical
propositions actually follow when the
conditions specified in the same
proposition(s) pertain. If the test fails, return
to step 2, otherwise go to step 4.
4. Accept the hypothesis as provisionally
true. Return to step 3 if you can conceive
any other case which may show the
answer to be defective.
4. Accept the hypothesis as provisionally true.
Return to step 3 if there are predictable
consequences of the theory which have not
been experimentally confirmed.
5. Act accordingly.
5. Act accordingly.
47
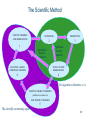
The Scientific Method
EXISTING THEORIES
AND OBSERVATIONS
HYPOTHESIS
PREDICTIONS
2
3
1
Hypothesis
must be
redefined
Hypotesen
Hypothesis
måste
must
be
justeras
adjusted
SELECTION AMONG
COMPETING THEORIES
TESTS AND NEW
OBSERVATIONS
6
4
Consistency achieved
The hypotetico-deductive cycle
EXISTING THEORY CONFIRMED
(within a new context) or
NEW THEORY PUBLISHED
5
The scientific-community cycle
48
The Scientific Method
Formulating Research Questions and Hypotheses
Different approaches:
Intuition – (Educated) Guess
Analogy
Symmetry
Paradigm
Metaphor
and many more ..
49
The Scientific Method
Criteria to Evaluate Theories
When there are several rivaling hypotheses number of criteria can
be used for choosing a best theory.
Following can be evaluated:
– Theoretical scope
– Heuristic value (heuristic: rule-of-thumb or argument
derived from experience)
– Parsimony (simplicity, Ockham’s razor)
– Esthetics
– Etc.
50
The Scientific Method
Criteria which Good Scientific Theory Shall Fulfill
–
–
–
–
–
–
–
–
Logically consistent
Consistent with accepted facts
Testable
Consistent with related theories
Interpretable: explain and predict
Parsimonious
Pleasing to the mind (Esthetic, Beautiful)
Useful (Relevant/Applicable)
51
The Scientific Method
Ockham’s Razor (Occam’s Razor)
(Law Of Economy, Or Law Of Parsimony, Less Is More!)
A philosophical statement developed by William of Ockham,
(1285–1347/49), a scholastic, that Pluralitas non est ponenda
sine necessitate; “Plurality should not be assumed without
necessity.”
The principle gives precedence to simplicity; of two competing
theories, the simplest explanation of an entity is to be preferred.
52
Science as a result of Scientific Community
MAP OF SCIENCE
http://www.lanl.gov/news/albums/science/PL
OSMapOfScience.jpg
This "Map of Science" illustrates
the online behavior of scientists
accessing different scientific
journals, publications, aggregators,
etc. Colors represent the scientific
discipline of each journal, based on
disciplines
http://www.lanl.gov/news/index.php/fuseaction/nb.story/story_id/%2015965
53
Knowledge
54
What is Knowledge?
Plato´s Definition
Plato believed that we learn in this life by remembering knowledge
originally acquired in a previous life, and that the soul already
has knowledge, and we learn by recollecting what in fact the
soul already knows.
[At present we know that we inherit some physical preconditions,
structures and abilities already at birth. In a sense those
structures of our brains and bodies may be seen as the result of
evolution, so in a sense they encapsulate memories of the
historical development of our bodies.]
55
What is Knowledge?
Plato´s Definition
Plato offers three analyses of knowledge, [dialogues Theaetetus
201 and Meno 98] all of which Socrates rejects.
Plato's third definition:
" Knowledge is justified, true belief. "
The problem with this concerns the word “justified”. All
interpretations of “justified” are deemed inadequate.
Edmund Gettier, in the paper called "Is Justified True Belief
Knowledge?“ argues that knowledge is not the same as justified
true belief. (Gettier Problem)
56
What is Knowledge?
Descartes´ Definition
"Intuition is the undoubting conception of an unclouded and
attentive mind, and springs from the light of reasons alone; it is
more certain than deduction itself in that it is simpler."
“Deduction by which we understand all necessary inference from
other facts that are known with certainty,“ leads to knowledge
when recommended method is being followed.
57
What is Knowledge?
Descartes´ Definition
"Intuitions provide the ultimate grounds for logical deductions.
Ultimate first principles must be known through intuition while
deduction logically derives conclusions from them.
These two methods [intuition and deduction] are the most certain
routes to knowledge, and the mind should admit no others."
58
What is Knowledge?
– Propositional knowledge: knowledge that such-and-such is the
case.
– Non-propositional knowledge (tacit knowledge): the knowing how to
do something.
59
Sources of Knowledge
– A Priori Knowledge (built in, developed by evolution and
inheritance) (resides the brain as memory)
– Perception (“on-line input”, information acquisition)
– Reasoning (information processing)
– Testimony (network, communication)
60
Blurring the Boundary Between
Perception and Memory
http://www.scientificamerican.com/article.cfm?id=perc
eption-and-memory
http://www.sciencedaily.com
61
62
Blue Brain vs Map of Science
http://online.wsj.com/article/SB124751881557234725.html
In Search for Intelligence, a Silicon Brain Twitches
63
Computational Brain
Brain Processing Information
64
Cell Processing Information
http://www.youtube.com/watch?v=BtZEqQ1cpmk&feature=related
BioVisions – The Inner Life of the Cell - Harvard University
http://www.goldenswamp.com/page/2/
65
Knowledge and Justification
Knowledge and Objectivity: Observations
Observations are always interpreted in the context of an a priori
knowledge. (Kuhn, Popper)
“What a man sees depends both upon what he looks at and also
upon what his previous visual-conceptual experience has taught
him to see”.
66
Knowledge and Objectivity
Observations
– All observation is potentially ”contaminated”, whether by our
theories, our worldview or our past experiences.
– It does not mean that science cannot ”objectively” [intersubjectivity] choose from among rival theories on the basis of
empirical testing.
– Although science cannot provide one with hundred percent
certainty, yet it is the most, if not the only, objective mode of
pursuing knowledge.
67
Perception and “Direct Observation”
68
Perception and “Direct Observation”
69
Perception and “Direct Observation”
70
Perception and “Direct Observation”
71
Perception and “Direct Observation”
"Reality is merely an illusion,
albeit a very persistent one." Einstein
72
73
Perception and “Direct Observation”
Checker-shadow illusion
http://web.mit.edu/persci/people/adelson/checkershadow_illusion.html
See even:
http://web.mit.edu/persci/gaz/gaz-teaching/index.html
http://persci.mit.edu/people/adelson/publications/gazzan.dir/gazzan.htm
Lightness Perception and Lightness Illusions
74
Direct Observation?!
An atom interferometer, which splits an atom into separate wavelets, can allow
the measurement of forces acting on the atom. Shown here is the laser
system used to coherently divide, redirect, and recombine atomic wave
packets (Yale University).
75
Direct Observation?!
Electronic signatures
produced by collisions of
protons and antiprotons in
the Tevatron accelerator
at Fermilab provided
evidence that the elusive
subatomic particle known
as top quark has been
found.
76
Knowledge Justification
– Foundationalism (uses architectural metaphor to describe the
structure of our belief systems. The superstructure of a belief
system inherits its justification from a certain subset of beliefs –
all rests on basic beliefs.)
– Coherentism
– Internalism (a person has “cognitive grasp”) and Externalism
(external justification)
77
Truth (1)
– The correspondence theory
– The coherence theory
– The deflationary theory
78
Truth (2)
The Correspondence Theory
A common intuition is that when I say something true, my
statement corresponds to the facts.
But: how do we recognize facts and what kind of relation is this
correspondence?
79
Truth (3)
The Coherence Theory
Statements in the theory are believed to be true because being
compatible with other statements.
The truth of a sentence just consists in its belonging to a system of
coherent statements.
The most well-known adherents to such a theory was Spinoza
(1632-77), Leibniz (1646-1716) and Hegel (1770-1831).
Characteristically they all believed that truths about the world could
be found by pure thinking, they were rationalists and idealists.
Mathematics was the paradigm for a real science; it was
thought that the axiomatic method in mathematics could be
used in all sciences.
80
Truth (4)
The Deflationary Theory
The deflationary theory is belief that it is always logically
superfluous to claim that a proposition is true, since this claim
adds nothing further to a simple affirmation of the proposition
itself.
"It is true that birds are warm-blooded " means the same thing as
"birds are warm-blooded ".
For the deflationist, truth has no nature beyond what is captured in
ordinary claims such as that ‘snow is white’ is true just in case
snow is white.
81
Truth (5)
The Deflationary Theory
The Deflationary Theory is also called the redundancy
theory, the disappearance theory, the no-truth theory,
the disquotational theory, and the minimalist theory .
63-70 see Lars-Göran Johansson
http://www.filosofi.uu.se/utbildning/Externt/slu/slultexttruth.htm
and Stanford Encyclopedia of Philosophy
http://plato.stanford.edu/entries/truth-deflationary/
82
Truth and Reality
Noumenon,"Ding an sich" is
distinguished from
Phenomenon "Erscheinung", an
observable event or physical
manifestation, and the two words
serve as interrelated technical
terms in Kant's philosophy.
83
Whole vs. Parts
•
•
•
•
•
tusk  spear
tail  rope
trunk  snake
side  wall
leg  tree
The flaw in all their reasoning is that speculating on the
WHOLE from too few FACTS can lead to VERY
LARGE errors in judgment.
84
Science and Truth
– Science as controversy (new science, frontiers)
– Science as consensus (old, historically settled)
– Science as knowledge about complex systems
– Opens systems, paraconsistent logic
85
Proof
The word proof can mean:
• originally, a test assessing the validity or quality of something.
Hence the saying, "The exception that proves the rule" -- the
rule is tested to see whether it applies even in the case of the
(apparent) exception.
• a rigorous, compelling argument, including:
– a logical argument or a mathematical proof
– a large accumulation of scientific evidence
– (...)
(from Wikipedia)
86
Mathematical Proof
In mathematics, a proof is a demonstration that, given certain
axioms, some statement of interest is necessarily true.
(from Wikipedia)
87
Mathematical Proof
Proofs employ logic but usually include some amount of natural
language which of course admits some ambiguity. In the context
of proof theory, where purely formal proofs are considered, such
not entirely formal demonstrations are called "social proofs".
The distinction has led to much examination of current and historical
mathematical practice, quasi-empiricism in mathematics, and socalled folk mathematics (in both senses of that term).
The philosophy of mathematics is concerned with the role of
language and logic in proofs, and mathematics as a language.
(from Wikipedia)
88
Mathematical Proof
Regardless of one's attitude to formalism, the result that is proved
to be true is a theorem; in a completely formal proof it would be
the final line, and the complete proof shows how it follows from
the axioms alone. Once a theorem is proved, it can be used as
the basis to prove further statements.
The so-called foundations of mathematics are those statements
one cannot, or need not, prove. These were once the primary
study of philosophers of mathematics. Today focus is more on
practice, i.e. acceptable techniques.
(from Wikipedia)
89
Pressupositions and Limitations
of Axiomatic Logical Systems
Axiomatic theory is built on a set of few axioms/postulates
(ideas which are considered so elementary and manifestly
obvious that they do not need to be proven as any proof would
introduce more complex ideas).
All the theorems (true statements) are derived logically from the
axioms.
When a system requires increasing number of axioms (as e.g.
number theory does), doubts begin to arise. How many axioms
are needed? How do we know that the axioms aren't mutually
contradictory? Each new axiom can change the meaning of the
previous system.
90
GÖDEL: TRUTH AND PROVABILITY (1)
Kurt Gödel actually proved two extraordinary theorems. They have
revolutionized mathematics, showing that mathematical truth is
more than bare logic and computation.
Gödel has been called the most important logician since Aristotle.
His two theorems changed logic and mathematics as well as the
way we look at truth and proof.
91
GÖDEL: TRUTH AND PROVABILITY (2)
Gödels first theorem proved that any formal system strong enough
to support number theory has at least one undecidable
statement. Even if we know that the statement is true, the
system cannot prove it. This means the system is incomplete.
For this reason, Gödel's first proof is called "the incompleteness
theorem".
92
GÖDEL: TRUTH AND PROVABILITY (3)
Gödel's second theorem is closely related to the first. It says that no
one can prove, from inside any complex formal system, that it is
self-consistent.
"Gödel showed that provability is a weaker notion than truth, no
matter what axiomatic system is involved.
In other words, we simply cannot prove some things in
mathematics (from a given set of premises) which we
nonetheless can know are true. “ (Hofstadter)
93
TRUTH VS. PROVABILITY
ACCORDING TO GÖDEL
After: Gödel, Escher, Bach - an Eternal Golden Braid
by Douglas Hofstadter.
94
TRUTH VS. PROVABILITY
ACCORDING TO GÖDEL
Gödel theorem is built upon Aristotelian logic.
So it is true within the paradigm of Aristotelian logic.
However, nowadays it is not the only logic existing.
95
LOGIC (1)
The precision, clarity and beauty of mathematics are the
consequence of the fact that the logical basis of classical
mathematics possesses the features of parsimony and
transparency.
Classical logic owes its success in large part to the efforts of
Aristotle and the philosophers who preceded him. In their
endeavour to devise a concise theory of logic, and later
mathematics, they formulated so-called "Laws of Thought".
96
LOGIC (2)
One of these, the "Law of the Excluded Middle," states that every
proposition must either be True or False.
When Parminedes proposed the first version of this law (around
400 B.C.) there were strong and immediate objections.
For example, Heraclitus proposed that things could be
simultaneously True and not True.
97
NON-STANDARD LOGIC
FUZZY LOGIC (1)
Plato laid the foundation for fuzzy logic, indicating that there was a
third region (beyond True and False).
Some among more modern philosophers follow the same path,
particularly Hegel.
But it was Lukasiewicz who first proposed a systematic alternative
to the bi-valued logic of Aristotle.
98
NON-STANDARD LOGIC
FUZZY LOGIC (2)
In the early 1900's, Lukasiewicz described a three-valued logic,
along with the corresponding mathematics.
The third value "possible," assigned a numeric value between True
and False.
Eventually, he proposed an entire notation and axiomatic system
from which he hoped to derive modern mathematics.
99
NON-STANDARD LOGICS
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
Categorical logic
Combinatory logic
Conditional logic
Constructive logic
Cumulative logic
Deontic logic
Dynamic logic
Epistemic logic
Erotetic logic
Free logic
Fuzzy logic
Higher-order logic
Infinitary logic
Intensional logic
Intuitionistic logic
Linear logic
•
•
•
•
•
•
•
•
•
•
•
•
•
•
Many-sorted logic
Many-valued logic
Modal logic
Non-monotonic logic
Paraconsistent logic
Partial logic
Prohairetic logic
Quantum logic
Relevant logic
Stoic logic
Substance logic
Substructural logic
Temporal (tense) logic
Other logics
100
Meaning (1)
All meaning is determined by the method of analysis where the
method of analysis sets the context and so the rules that are
used to determine the “meaningful” from “meaningless”.
C. J. Lofting
101
Meaning (2)
At the fundamental level meaning is reducible to distinguishing
• Objects (the what) from
• Relationships (the where)
which are the result of process of
• Differentiation or
• Integration
102
Meaning (3)
Human brain is not tabula rasa (clean slate) on birth but rather
contains
• behavioral patterns to particular elements of environment (genebased)
• template used for distinguishing meaning based on the distinctions
of “what” from “where”
• Meaning as use implies holistic rationality, and value systems
(hence ethical views) are integrated in the aims of a rational agents.
103
http://ndpr.nd.edu/review.cfm?id=12083 Notre Dame Philosophical Reviews
104
Philosophy of Science/Theory of Science
Assignments
– Assignment 2: Demarcation of Science vs.
Pseudoscience (in groups of two)
– Discussion of Assignment 2 - compulsory
– Assignment 2-extra (For those who miss the discussion of the
Assignment 2)
– Assignment 3: GOLEM: Three Cases of Theory
Confirmation (in groups of two)
– Discussion of Assignment 3 - compulsory
– Assignment 3-extra (For those who miss the discussion of the
Assignment 3)
105
Two Examples of Axiomatic Systems Limitations and Developments
106
Pressupositions and Limitations
of Formal Logical Systems
Axiomatic System of Euclid: Shaking up Geometry
Euclid built geometry on a set of few axioms/postulates (ideas
which are considered so elementary and manifestly obvious that
they do not need to be proven as any proof would introduce
more complex ideas).
When a system requires increasing number of axioms (as e.g.
number theory does), doubts begin to arise. How many axioms
are needed? How do we know that the axioms aren't mutually
contradictory?
107
Pressupositions and Limitations
of Formal Logical Systems
Axiomatic System of Euclid: Shaking up Geometry
Until the 19th century no one was too concerned about
axiomatization.
Geometry had stood as conceived by Euclid for 2100 years.
If Euclid's work had a weak point, it was his fifth axiom, the axiom
about parallel lines. Euclid said that for a given straight line, one
could draw only one other straight line parallel to it through a
point somewhere outside it.
108
EUCLID'S AXIOMS (1)
1. Every two points lie on exactly one line.
2. Any line segment with given endpoints may be continued in
either direction.
3. It is possible to construct a circle with any point as its center and
with a radius of any length. (This implies that there is neither an
upper nor lower limit to distance. In-other-words, any distance,
no mater how large can always be increased, and any distance,
no mater how small can always be divided.)
109
EUCLID'S AXIOMS (2)
4. If two lines cross such that a pair of adjacent angles are
congruent, then each of these angles are also congruent to any
other angle formed in the same way. (Says that all right angles
are equal to one another.)
5. (Parallel Axiom): Given a line l and a point not on l, there is one
and only one line which contains the point, and is parallel to l.
110
NON-EUCLIDEAN GEOMETRIES (1)
Mid-1800s: mathematicians began to experiment with different
definitions for parallel lines.
Lobachevsky, Bolyai, Riemann: new non-Euclidean geometries by
assuming that there could be several parallel lines through the
outside point or there could be no parallel lines.
111
NON-EUCLIDEAN GEOMETRIES (2)
Two ways to negate the Euclidean Parallel Axiom:
– 5-S (Spherical Geometry Parallel Axiom): Given a line l and a
point not on l, no lines exist that contain the point, and are parallel
to l.
– 5-H (Hyperbolic Geometry Parallel Axiom): Given a line l and a
point not on l, there are at least two distinct lines which contains
the point, and are parallel to l.
112
Reproducing the Euclidean World
in a model of the Elliptical Non-Euclidean World.
113
Spherical/Elliptical Geometry
In spherical geometry lines of latitude are not great circles (except for
the equator), and lines of longitude are. Elliptical Geometry takes the
spherical plan and removes one of two points directly opposite each
other. The end result is that in spherical geometry, lines always intersect
in exactly two points, whereas in elliptical geometry, lines always
intersect in one point.
114
Properties of Elliptical/Spherical Geometry
In Spherical Geometry, all lines intersect in 2 points. In elliptical
geometry, lines intersect in 1 point.
In addition, the angles of a triangle always add up to be greater
than 180 degrees. In elliptical/spherical geometry, all of Euclid's
postulates still do hold, with the exception of the fifth postulate.
This type of geometry is especially useful in describing the Earth's
surface.
115
Hyperbolic Cubes
116
DEFINITION:
Parallel lines are infinite lines in the same plane that do not intersect.
Hyperbolic Universe
Flat Universe
Spherical Universe
Einstein incorporated Riemann's ideas into relativity theory to
describe the curvature of space.
117
MORE PROBLEMS WITH
AXIOMATIZATION…
Not only had Riemann created a system of geometry which put
commonsense notions on its head, but the philosophermathematician Bertrand Russell had found a serious paradox
for set theory!
He has shown that Frege’s attempt to reduce mathematics to
logical reasoning starting with sets as basics leads to
contradictions.
118
HILBERT’S PROGRAM
Hilbert’s hope was that mathematics would be reducible to finding
proofs (by manipulating the strings of symbols) from a fixed
system of axioms, axioms that everyone could agree were true.
Can all of mathematics be made algorithmic, or will there always be
new problems that outstrip any given algorithm, and so require
creative mind to solve?
119
AXIOMATIC SYSTEM OF PRINCIPIA:
PARADOX IN SET THEORY
Mathematicians hoped that Hilbert's plan would work because
axioms and definitions are based on logical commonsense
intuitions, such as e.g. the idea of set.
A set is any collection of items chosen for some characteristic
common for all its elements.
120
RUSSELL'S PARADOX (1)
There are two kinds of sets:
– Normal sets, which do not contain themselves, and
– Non-normal sets, which are sets that do contain themselves.
The set of all apples is not an apple. Therefore it is a normal set. The
set of all thinkable things is itself thinkable, so it is a non-normal set.
121
RUSSELL'S PARADOX (2)
Let 'N' stand for the set of all normal sets.
Is N a normal set?
If it is a normal set, then by the definition of a normal set it
cannot be a member of itself. That means that N is a non-normal
set, one of those few sets which actually are members of
themselves.
122
RUSSELL'S PARADOX (3)
But on the other hand…N is the set of all normal sets; if we
describe it as a non-normal set, it cannot be a member of itself,
because its members are, by definition, normal.
123
RUSSELL'S PARADOX (4)
Russell resolved the paradox by redefining the meaning of 'set' to
exclude peculiar (self-referencing) sets, such as "the set of all
normal sets“.
Together with Whitehead in Principia Mathematica he founded
mathematics on that new set definition.
They hoped to get self-consistent and logically coherent system …
124
RUSSELL'S PARADOX (5)
… However, even before the project was complete, Russell's
expectations were dashed!
The man who showed that Russell's aim was impossible was Kurt
Gödel, in a paper titled "On Formally Undecidable Propositions
of Principia Mathematica and Related Systems."
125
Critique of Usual Naïve Image
of Scientific Method
126
Critique of Usual Naïve Image
of Scientific Method (1)
The narrow inductivist conception of scientific inquiry
1. All facts are observed and recorded.
2. All observed facts are analyzed, compared and classified,
without hypotheses or postulates other than those necessarily
involved in the logic of thought.
3. Generalizations inductively drawn as to the relations,
classificatory or causal, between the facts.
4. Further research employs inferences from previously
established generalizations.
127
Critique of Usual Naïve Image
of Scientific Method (2)
This narrow idea of scientific inquiry is groundless for several
reasons:
1. A scientific investigation could never get off the ground, for a
collection of all facts would take infinite time, as there are infinite
number of facts.
The only possible way to do data collection is to take only relevant
facts. But in order to decide what is relevant and what is not, we
have to have a theory or at least a hypothesis about what is it we
are observing.
128
Critique of Usual Naïve Image
of Scientific Method (3)
A hypothesis (preliminary theory) is needed to give the direction
to a scientific investigation!
2. A set of empirical facts can be analyzed and classified in many
different ways. Without hypothesis, analysis and classification
are blind.
3. Induction is sometimes imagined as a method that leads, by
mechanical application of rules, from observed facts to general
principles. Unfortunately, such rules do not exist!
129
Why is it not possible to derive hypothesis
(theory) directly from the data? (1)
– For example, theories about atoms contain terms like “atom”,
“electron”, “proton”, etc; yet what one actually measures are
spectra (wave lengths), traces in bubble chambers, calorimetric
data, etc.
– So the theory is formulated on a completely different (and more
abstract) level than the observable data!
– The transition from data to theory requests creative imagination!
130
Why is it not possible to derive hypothesis
(theory) directly from the data?* (2)
– Scientific hypothesis is formulated based on “educated guesses”
at the connections between the phenomena under study, at
regularities and patterns that might underlie their occurrence.
Scientific guesses are completely different from any process of
systematic inference.
– The discovery of important mathematical theorems, like the
discovery of important theories in empirical science, requires
inventive ingenuity.
*Here is instructive to study Automated discovery methods in order to see how
much theory must be used in order to extract meaning from the “raw data”
131