Download Intermolecular Interactions

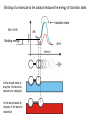
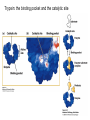
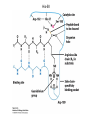
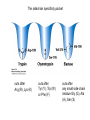
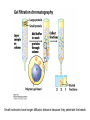
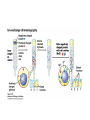
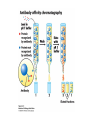
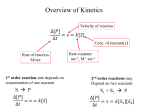
Lecture 7
Brief review of enzyme mechanisms and kinetics
A ‘toolbox’ for mechanistic biochemists. A path to
the molecule: protein purification techniques.
Protein Kinase A spatially organizes ATP and peptide chain
to facilitate the reaction
Rate of ‘hopping’
over the barrier:
k BT  DG  / k BT
k
e
h
kB – Boltzmann constant
frequency
pre-factor
Boltzmann
factor
h – Plank constant
DG*s→p
DG*p→s
DG o
Binding of a molecule to the catalyst reduces the energy of transition state
transition state
AA = A+A
Binding energy
In the bound state to
enzyme I the bond is
relaxed (no catalysis)
In the bound state to
enzyme II the bond is
stretched
AA
A+A
Trypsin: the binding pocket and the catalytic site
His58
Asp102
Ser195
Asp189
His58
Asp102
Ser195
Asp189
His-58
The sidechain specificity pocket
cuts after
Arg (R), Lys (K)
cuts after
Tyr (Y), Trp (W)
or Phe (F)
cuts after
any small side-chain
residue Gly (G), Ala
(A), Ser (S)
Catalysis involves simple binding
L  R  LR
K b [ L]
B
1  K b [ L]
1
Kd 
Kb
[ L]
B
K d  [ L]
Langmuir
Michaelis-Menten equation for enzyme/transport
reactions is very similar to the Langmuir isotherm
V  Vmax
[ s]
K m  [ s]
Vmax 1
Km = 1 mM
0.8
Km = 10 mM
0.6
0.4
0.2
0
0
10
20
30
[s], mM
40
50
A “simple explanation” says
that the rate of reaction should
be proportional to the
occupancy of the binding site
as long as Vmax is constant.
Rate of ‘hopping’
over the barrier:
k BT  DG  / k BT
k
e
h
DG*uncat
E+S
DG*cat
E+P
E + S ↔ ES ↔ EP ↔ E + P
k1
k2
E + S ↔ ES → E + P
(we assume k-2 = 0 )
k-1
Et – total enzyme
d [ES]
 k1 ([ Et ]  [ES])[S]  (k 1[ES]  k 2 [ES])
dt
Rate of ES formation
At steady state:
d [ES]
0
dt
k 1  k 2
Km 
k1
k 2 [Et][S]
V
K m  [S]
Rate of ES breakdown
k1[Et ][S]
[ES] 
k1[S]  k 1  k 2
V  k2 [ES]
Vmax [S]
V
K m  [S]
Vmax  k2 [Et ]
Michaelis-Menten again
How do we know who are the players in the structural assembly,
reaction of interest or specific signaling cascade?
1. Standard biochemical ‘brute-force’ approach: isolate/purify the
protein component(s) and show that they are functional or necessary
for the specific function; then clone the gene(s), mutate or knock them
out (down) and demonstrate altered function (biochemistry+reverse
genetics).
2. Genetic approach: mutagenize and see the phenotypic deviation,
find the mutant, identify and clone the gene conferring that specific
trait, predict its product, generate the knock-out and show the
interdependence between the phenotype and the presence of intact
gene coding for that protein (forward genetics).
3. A reductionistic finale of either path toward the molecule: for
most of the mechanistic studies it is important to express and isolate
that protein, find the conditions under which it is active in isolation,
reconstitute its functional state in a test tube and determine its
properties in vitro. Obtain structural and mechanistic clues on how the
molecular machine works.
Cell disruption and fractionation
2D gels separate first by charge an then by size
Small molecules have longer diffusion distance because they penetrate the beads
Western Blotting
Mass spectrometry
measures
m/z
(mass/charge)
Complete sequencing of a protein can be accomplished using MS/MS in
conjunction with genomic information