* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download ppt
Pharmacogenomics wikipedia , lookup
History of genetic engineering wikipedia , lookup
Genetic drift wikipedia , lookup
Gene expression programming wikipedia , lookup
Designer baby wikipedia , lookup
Human genetic variation wikipedia , lookup
Population genetics wikipedia , lookup
Genetic engineering wikipedia , lookup
Microevolution wikipedia , lookup
Quantitative trait locus wikipedia , lookup
Fetal origins hypothesis wikipedia , lookup
Public health genomics wikipedia , lookup
Genetic testing wikipedia , lookup
Genome (book) wikipedia , lookup
Biology and consumer behaviour wikipedia , lookup
Behavioural genetics wikipedia , lookup
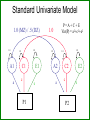
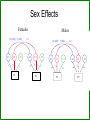
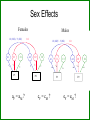
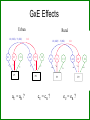
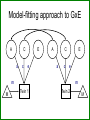
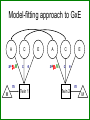
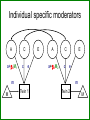
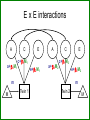
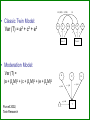
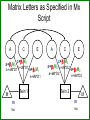
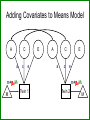
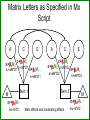
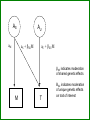
Gene-Environment Interaction & Correlation Danielle Dick & Tim York VCU workshop, Fall 2010 Gene-Environment Interaction • Genetic control of sensitivity to the environment • Environmental control of gene expression • Bottom line: nature of genetic effects differs among environments Standard Univariate Model 1.0 (MZ) / .5 (DZ) 1.0 1.0 1.0 A1 a C1 c P1 1.0 1.0 E1 e P=A+ C + E Var(P) = a2+c2+e2 1.0 1.0 A2 a C2 c E2 e P2 Contributions of Genetic, Shared Environment, Genotype x Environment Interaction Effects to Twin/Sib Resemblance Shared Environment Additive Genetic Effects Genotype x Shared Environment Interaction MZ Pairs 1 1 1x1=1 DZ Pairs/Full Sibs 1 ½ 1x½=½ Contributions of Genetic, Shared Environment, Genotype x Shared Environment Interaction Effects to Twin/Sib Resemblance Shared Environment Additive Genetic Effects Genotype x Shared Environment Interaction MZ Pairs 1 1 1x1=1 DZ Pairs/Full Sibs 1 ½ 1x½=½ In other words—if gene-(shared) environment interaction is not explicitly modeled, it will be subsumed into the A term in the classic twin model. Contributions of Genetic, Unshared Environment, Genotype x Unshared Environment Interaction Effects to Twin/Sib Resemblance Unshared (Unique) Environment Additive Genetic Effects Genotype x Unshared Environment Interaction MZ Pairs 0 1 0x1=0 DZ Pairs/Full Sibs 0 ½ 0x½=0 If gene-(unshared) environment interaction is not explicitly modeled, it will be subsumed into the E term in the classic twin model. Ways to Model Gene-Environment Interaction in Twin Data • Multiple Group Models – (parallel to testing for sex effects using multiple groups) Sex Effects Females 1.0 (MZ) / .5 (DZ) A1 aF C1 cF P1 E1 eF Males 1.0 1.0 (MZ) / .5 (DZ) A2 aF C2 cF P2 E2 eF A1 aM C1 cM P1 E1 eM 1.0 A2 aM C2 cM P2 E2 eM Sex Effects Females 1.0 (MZ) / .5 (DZ) A1 aF C1 cF E1 eF P1 aF = aM ? Males 1.0 1.0 (MZ) / .5 (DZ) A2 aF C2 cF E2 A1 eF P2 aM C1 cM E1 eM 1.0 A2 aM P1 cF = cM ? C2 cM P2 eF = eM ? E2 eM GxE Effects Urban 1.0 (MZ) / .5 (DZ) A1 aF C1 cF E1 eF P1 aU = aR ? Rural 1.0 1.0 (MZ) / .5 (DZ) A2 aF C2 cF E2 A1 eF P2 aM C1 cM E1 eM 1.0 A2 aM P1 cU = cR ? C2 cM P2 eU = eR ? E2 eM Practical: Using Multiple Group Models to test for GxE Problem: • Many environments of interest do not fall into groups – Regional alcohol sales – Parental warmth – Parental monitoring – Socioeconomic status • Grouping these variables into high/low categories loses a lot of information ‘Definition variables’ in Mx • General definition: Definition variables are variables that may vary per subject and that are not dependent variables • In Mx: The specific value of the def var for a specific individual is read into a matrix in Mx when analyzing the data of that particular individual ‘Definition variables’ in Mx create dynamic var/cov structure • Common uses: 1. To model changes in variance components as function of some variable (e.g., age, SES, etc) 2. As covariates/effects on the means (e.g. age and sex) Standard model • Means vector m m • Covariance matrix a c e Za 2 c 2 2 2 2 2 2 2 a c e Model-fitting approach to GxE A C a c E e A C a c E e m M m Twin 1 Twin 2 M Model-fitting approach to GxE A a+XM m M C c E e Twin 1 A a+XM C c E e Twin 2 m M Individual specific moderators A a+XM1 C c E e A a+XM2 C c E e m M m Twin 1 Twin 2 M E x E interactions A a+XM1 C E c+YM1 e+ZM1 A a+XM2 C c+YM2 e+ZM2 m M E m Twin 1 Twin 2 M 1.0 (MZ) / .5 (DZ) • Classic Twin Model: Var (T) = a2 + c2 + e2 A1 a C1 c E1 e 1.0 A2 C2 a c Twin 1 E2 e Twin 2 • Moderation Model: Var (T) = (a + βXM)2 + (c + βYM)2 + (e + βZM)2 A a + βXM C e + βZM c + βyM + βMM Purcell 2002, Twin Research E T Var (T) = (a + βXM)2 + (c + βYM)2 (e + βZM)2 Where M is the value of the moderator and Significance of βX indicates genetic moderation Significance of βY indicates common environmental moderation Significance of βZ indicates unique environmental moderation BM indicates a main effect of the moderator on the mean A a + βXM C E e + βZM c + βyM + βMM T Matrix Letters as Specified in Mx Script A C E a+XM1 c+YM1 a +aM*D1 c+cM*D1 e+ M Z 1 Twin 1 C E c+YM2 e+eM*D1 M A a+XM2 c+cM*D2 e+ M Z 2 a+aM*D2 e+eM*D2 Twin 2 M m m mu mu Practical: Using Definition Variables to test for GxE Additional Things to Consider • Unstandardized versus standardized effects Additional Things to Consider Unstandardized versus standardized effects ENVIRONMENT 1 ENVIRONMENT 2 Unstandardized Variance Standardized Variance Unstandardized Variance Standardized Variance Genetic 60 0.60 60 0.30 Common environmental 35 0.35 70 0.35 Unique environmental 5 0.05 70 0.05 Total variance 100 200 ‘Definition variables’ in Mx create dynamic var/cov structure • Common uses: 1. To model changes in variance components as function of some variable (e.g., age, SES, etc) 2. As covariates/effects on the means (e.g. age and sex) Definition variables used as covariates General model with age and sex as covariates: yi = + 1(agei) + 2 (sexi) + Where yi is the observed score of individual i, is the intercept or grand mean, 1 is the regression weight of age, agei is the age of individual i, 2 is the deviation of males (if sex is coded 0= female; 1=male), sexi is the sex of individual i, and is the residual that is not explained by the covariates (and can be decomposed further into ACE etc). Allowing for a main effect of X • Means vector m X1i m X 2 i • Covariance matrix a c e Za 2 c 2 2 2 2 2 2 2 a c e Common uses of definition variables in the means model • Incorporating covariates (sex, age, etc) • Testing the effect of SNPs (association) • In the context of GxE, controlling for rGE Gene-environment Interaction • Genetic control of sensitivity to the environment • Environmental control of gene expression Gene-environment Correlation • Genetic control of exposure to the environment • Environmental control of gene frequency This complicates interpretation of GxE effects • If there is a correlation between the moderator (environment) of interest and the outcome, and you find a GxE effect, it’s not clear if: – The environment is moderating the effects of genes or – Trait-influencing genes are simply more likely to be present in that environment Adding Covariates to Means Model A C a c E e A C a c E e m+MM1 M m+MM2 Twin 1 Twin 2 M Matrix Letters as Specified in Mx Script A C E a+XM1 c+YM1 a +aM*D1 e+eM*D1 Twin 1 C a+XM2 c+cM*D2 e+ M Z 2 a+aM*D2 e+eM*D2 Twin 2 M m+MM2 m+MM1 mu+b*D1 E c+YM2 c+cM*D1 e+ M Z 1 M A Main effects and moderating effects mu+b*D2 Ways to deal with rGE • Limit study to moderators that aren’t correlated with outcome – Pro: easy – Con: not very satisfying • Moderator in means model will remove from the covariance genetic effects shared by trait and moderator – Pro: Any interaction detected will be moderation of the trait specific genetic effects – Con: Will fail to detect GxE interaction if the moderated genetic component is shared by the outcome and moderator • Explicitly model rGE using a bivariate framework – Pro: explicitly models rGE – Con: Power to detect BXU decreases with increasing rGE; difficulty converging AS aM AU aS + βXSM aU + βXUM βXS indicates moderation of shared genetic effects M T BXU indicates moderation of unique genetic effects on trait of interest