* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download 2 a - Atelier de BioInformatique
Rosetta@home wikipedia , lookup
Circular dichroism wikipedia , lookup
List of types of proteins wikipedia , lookup
Bimolecular fluorescence complementation wikipedia , lookup
Protein folding wikipedia , lookup
Protein design wikipedia , lookup
Western blot wikipedia , lookup
Intrinsically disordered proteins wikipedia , lookup
Protein mass spectrometry wikipedia , lookup
Protein purification wikipedia , lookup
Protein–protein interaction wikipedia , lookup
Protein domain wikipedia , lookup
Nuclear magnetic resonance spectroscopy of proteins wikipedia , lookup
Protein structure prediction wikipedia , lookup
IFBM 2004
Finding similarities in protein
structures:
a string approach
• Atelier de Bio-Informatique (ABI) - Université Paris VI
Searching for strict repeated patterns : KMR (1972)
k
k
2k
k
k
2k
- Occurrences of strictly repeated 2k-length
patterns are built from intersections of
sets of strictly repeated k-length patterns
which lie side-by-side
This leads to an O(n.log(kmax)) algorithm for
finding kmax-length repeated patterns
Flexible patterns : KMRC
• A pattern is no more defined as a succession of
symbols, instead it is a succession of cliques of
symbols
c1
a b c
c2
S
= caaaabaaacb
sC
2
2
= 21111111121
Here m is a repeated flexible pattern of length 3.
m = c1-c1-c2 at position 4 and 8
Note : several patterns may exist at the same position : here
c1-c1-c1 has also an occurrence in position 4
Flexible patterns : KMRC
• As in KMR, the 2-k length patterns are built from klength patterns.
• Here, a pattern is a clique of (similar) patterns, and
at one position in the string there may exist several
cliques of patterns.
The algorithm is now O(n.log(k).gk) (g being the mean degeneracy,
i.e. the mean number of cliques a symbol belongs to)
In biology, identity is trivial, similarity is interesting…
Flexible patterns in sequences (KMRC)
• This algorithm may be used to find flexible patterns
in several protein sequences (multiple alignment by
blocks):
p1
p2
p3
p4
p5
• Cliques of “symbols” define similarity, e.g :
- different overlapping sets of amino acids clustered by
their properties (e.g. hydrophobic, hydrophilic, small,
large, polar, charged, etc…)
- different overlapping sets of amino acids clustered by
setting a threshold value on their score in a similarity
matrix (e.g. BLOSUM or PAM)
PAM250
Threshold -> cliques
Similarity
is not
transitive !
Flexible patterns in structures (KMRC)
• Finding 3D structural patterns in several protein
structures
• Structures must be described as strings of symbols,
and similar structures must be composed of similar
symbols
• -> use of discretized internal coordinates (angles) as
an alphabet :
f,y
or
a,t angles
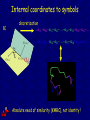
Internal coordinates a,t
Internal coordinates to symbols
a
discretization
...a21-a02-a13-a22-…-a19-a15-a20-a12-…
...a03-a21-a14-a21-…-a17-a16-a03-a22-…
Absolute need of similarity (KMRC), not identity !
Flexible patterns : KMRC
Finding flexible patterns of a -symbols :
Here, cliques of “symbols” are a angle overlapping sets
Similarity is a critical point (identity would miss
structural features).
-180°
0°
{a10 , a20 , a30 , a40 , a50 }
180°
{a20 , a30 , a40 , a50 , a60 }
Flexible patterns : KMRC
3 Cytochromes
P450:
TERP,BM3,CAM
PMWIATKHADVMQIG
VTRYLSSQRLIKEAC
GHWIATRGQLIREAY
PTHTAYRGLTLNWFQPASIRKLEENIRRIAQASVQR
KNWKKAHNILLPSFSQQAMKGYHAMMVDIAVQLVQK
PEQRQFRALANQVVGMPVVDKLENRIQELACSLIES
CDFMTDCALYYPLHVVMTALGVP
IEVPEDMTRLTLDTIGLCGFNYR
CNFTEDYAEPFPIRIFMLLAGLP
EDDEPLMLKLTQDF
ITSMVRALDEAMNK
EDIPHLKYLTDQMT
FHETIATFYDYFNGFTVDRRS
FQEDIKVMNDLVDKIIADRKA
FAEAKEALYDYLIPIIEQRRQ
CPKDDVMSLLAN
EQSDDLLTHMLN
KPGTDAISIVAN
Similarity : nature of elements OR relations between them
Bach BWV846
Similarity: series of notes with same pitch ?
-> transposed series rather…
Bach BWV846
-> Similarity of relations between elements
Bach BWV846
Relational patterns (KMRR)
• Now, a similar pattern is not defined by a
succession of similar symbols, but instead by
succession of elements that share the same
relationships between them.
r13
r12
Pattern m =
r13
r23
r12
r23
r13
r12 r23
Example of relations = “to be higher to”,
“to be lower to”, “to be equal to”,…
One step further : Flexible relational patterns
(KMRR)
• The relations between elements do not need to be
the same, they just need to be similar
rc
ra
ra
CR1
rb
rb
rb
rc
ra
Pattern m =
ra
CR2
CR1 CR1
CR2
Relational cliques
Cliques of relations = {“to be higher”, “to be equal”},
{“to be lower”, “to be equal”}…
An example: application to 3D structures:
relations are defined on discrete internal distances between points:
r(i,j) = rk if and only if rk ≤ dist(i,j) < rk + ∆
The relations r(i,j) and r(i’,j’) are considered as similar
if they belong to the same subset {rk, rk+1, rk+2}, i.e. if
| r(i, j) - r(i’, j’) | ≤ 2
This implies for euclidian distances :
| dist(i,j) - dist(i’,j’) | < 3∆
r1 r2 r3
rk rk+1 rk+2
d(i,j)
d(i ’,j’)
Application to 3D structures:
Relational cliques: 1 2 3 4 5 6 7 8 9 10 ….
(defined on distances)
Application to
3D structures:
Ex: multiple structural
alignment of 4 pectate and
pectin lyases:
1PCL,1IDJ,2BSP,1PLU
1PCL:
1IDJ:
2BSP:
1PLU:
AEWDAAVIDNSTNVWVDHVT
WGGDAITLDDCDLVWIDHVT
SQYDNITINGGTHIWIDHCT
KDGDMIRVDDSPNVWVDHNE
1PCL:
1IDJ:
2BSP:
1PLU:
LRVTFHNNVFDRVTERAPRV
DLVTMKGNYIYHTSGRSPKV
LKITLHHNRYKNIVQKAPRV
RNITYHHNYYNDVNARLPLQ
1PCL:
1IDJ:
2BSP:
1PLU:
TERAPRVRFGSIHAYNNVYL
GRSPKVQDNTLLHCVNNYFY
VQKAPRVRFGQVHVYNNYYE
NARLPLQRGGLVHAYNNLYT
1PCL:
1IDJ:
2BSP:
1PLU:
AQTMTSSLATSINNNAGYGK
SASAYTSVASRVVANAGQGN
SIDASANVKSNVINQAGAGK
SPVSAQCVKDKLPGYAGVGK
Structural similarity search
in databases: YAKUSA
database (PDB)
query
fast structural
scanning
Structural similarity search in databases: YAKUSA
Structures encoded with a angles
For each database protein:
1- find structural similar seeds with the query
2 - extend seeds to longer structural matches
Then rank the structural hits
Seeds of length k
All overlapping k-patterns of the query -> automaton
a1a1a2a1a2
Dictionary/Automaton
a1
a1
a1
a1
a2
a2
a1
a2
a2
a2
a2
Leaf->one seed
Advantage: no moving backward in the database string; less
moving backward in the patterns
Query seeds automaton
Dictionary/Automaton
with degeneracy with similar patterns
a'1
a1
dc(ai,a’i) < d
a2 a'2
a'1
a' 2
a2 a' 1
a1
a1
a1
a2
a'1
a2
'
a'2 a2 a 2
a'2
a1
a'1
a2
a1
a1
a'1
Sdc(ai, a’i) < D
a'2
a'1
a'2
a1
a2
a'1
a'2
a2
a'2 a
2
Matching seeds to SHSP
- (many seeds, giving only several SHSP)
seed
query
...a03-a21-a14-a21-a21-a22-a24-a17-a16-a03-a22-…
database ...a -a -a -a -a -a -a -a -a -a -a -…
21
02
11
24
22
23
23
19
14
20
12
SHSP
- SHSP=maximal scoring region around the
seed, the scores being based upon the angular
differences
- probability associated with SHSP (MTD: pair
approximation of Markov model)
SHSPs to results…
Database
structures
found,
ranked by
score
40 seconds for scanning 11000 PDB structures
http://bioserv.rpbs.jussieu.fr/Yakusa
Example of output:
query
(Deoxyribonuclease I)
database
(Heat-Shock protein 70)
SHSPs
http://bioserv.rpbs.jussieu.fr/Yakusa
Multiple structural alignment: « m-diagonals »
First step: finding pair “diagonals” (at the a angle level)
selection
of best 2diagonals
Index in first protein
Multiple structural alignment: « m-diagonals »
Second step: combination of 2-diagonals into m-diagonals
(in m dimensions).
Protein 1
Protein 2
Protein 3
m-diagonal in m dimensions :
here, the 3-diagonal is the
combination of three 2diagonals of dimension 2.
Multiple structural alignment: « m-diagonals »
Second step: combination of 2-diagonals into m-diagonals
(in m dimensions).
Protein 1
2
5
3
Protein 3
Protein 2
m-diagonal in m dimensions :
here, the 3-diagonal is the
combination of three 2diagonals of dimension 2.
Multiple structural alignment: « m-diagonals »
Second step: combination of 2-diagonals into m-diagonals
(in m dimensions).
“column” graphes :
- a residu is a node
- if two residues are in a 2diagonal, they are connected
by a link.
Protein 1
Protein 2
Protein 3
2
5
3
Selection of best m-diagonals (most connected ones)
Example:
13 cytochromes P450
- In blue : non aligned
parts
- Other colors :
m-diagonals
Other method :
« Gibbs sampling »
« Taboo search »
Kmrc+gok
Cytochromes P450
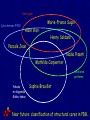
Marie-France Sagot
Alain Viari
Henry Soldano
Pascale Jean
Nadia Pisanti
Mathilde Carpentier
relational
patterns
Yakusa
m-diagonals
Gibbs-taboo
Sophie Brouillet
Near future: classification of structural cores in PDB…
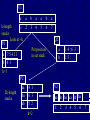
V1
a
a
b
a
a
b
a
k-length
1 2
stacks
Look at +k
P1
3
4
5
6
7
a 75421
b 6 3
Q2
Put position
in set stack
_a
_b
1 4;6 3
2 5;
k=1
P2
2k-length
stacks
aa
ba
ab
4 1
6 3
5 2
k=2
V2
aa ab ba aa ab ba
1
2
3
4
5
6
7