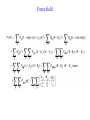* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Slide 1
G protein-gated ion channel wikipedia , lookup
Nuclear magnetic resonance wikipedia , lookup
X-ray crystallography wikipedia , lookup
Magnesium transporter wikipedia , lookup
Nuclear magnetic resonance spectroscopy wikipedia , lookup
G protein–coupled receptor wikipedia , lookup
Protein structure prediction wikipedia , lookup
Nuclear magnetic resonance spectroscopy of proteins wikipedia , lookup
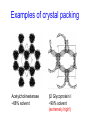
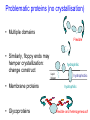
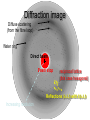
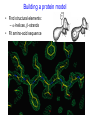
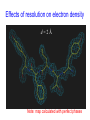
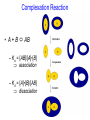
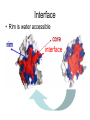
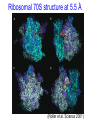
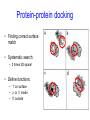
C E N T R E F O R I N T E G R A T I V E B I O I N F O R M A T I C S V U Experimentally solving protein structures, protein-protein interactions and simulating protein dynamics Lecture 15 Introduction to Bioinformatics 2007 Today’s lecture 1. Experimental techniques for determining protein tertiary structure 2. Protein interaction and docking i. Zdock method 3. Molecular motion simulated by molecular mechanics Experimentally solving protein structures Two basic techniques: 1. X-ray crystallography 2. Nuclear Magnetic Resonance (NMR) tchniques 1. X-ray crystallography Crystallization Purified protein Phase problem Crystal X-ray Diffraction Electron density Biological interpretation 3D structure Protein crystals • Regular arrays of protein molecules • ‘Wet’: 20-80% solvent • Few crystal contacts • Protein crystals contain active protein • Enzyme turnover • Ligand binding Example of crystal packing Examples of crystal packing Acetylcholinesterase ~68% solvent 2 Glycoprotein I ~90% solvent (extremely high!) Problematic proteins (no crystallisation) • Multiple domains Flexible • Similarly, floppy ends may hamper crystallization: change construct • Membrane proteins • Glycoproteins hydrophilic Lipid bilayer hydrophobic hydrophilic Flexible and heterogeneous!! Experimental set-up • Options for wavelength: – monochromatic, polychromatic – variable wavelength Liq.N2 gas stream X-ray source beam stop detector goniometer Diffraction image Diffuse scattering (from the fibre loop) Water ring Direct beam Beam stop reciprocal lattice (this case hexagonal) Reflections (h,k,l) with I(h,k,l) Increasing resolution The rules for diffraction: Bragg’s law • Scattered X-rays reinforce each other only when Bragg’s law holds: Bragg’s law: 2dhkl sin q = nl Building a protein model • Find structural elements: – -helices, -strands • Fit amino-acid sequence Building a protein model • Find structural elements: – -helices, -strands • Fit amino-acid sequence Effects of resolution on electron density d=4Å Note: map calculated with perfect phases Effects of resolution on electron density d=3Å Note: map calculated with perfect phases Effects of resolution on electron density d=2Å Note: map calculated with perfect phases Effects of resolution on electron density d=1Å Note: map calculated with perfect phases Validation • Free R-factor (cross validation) – This has to do with the number of parameters / observations • Ramachandran plot showing phi-psi angle distribution • Chemically likely (WhatCheck) – Hydrophobic inside, hydrophilic outside – Binding sites of ligands, metals, ions – Hydrogen-bonds satisfied – Chemistry in order • Final B-factor (temperature) values (colour coded in structure in the right) 2. Nuclear Magnetic Resonance (NMR) 800 MHz NMR spectrometer 2. NMR Purified protein Interpret map Distance geometry: resolve constraints Measure NOEs, etc. Distance constraints Biological interpretation Ensemble of 3D structures Nuclear Magnetic Resonance (NMR) • Pioneered by Richard R. Ernst, who won a Nobel Prize in chemistry in 1991. • FT-NMR works by irradiating the sample, held in a static external magnetic field, with a short square pulse of radio-frequency energy containing all the frequencies in a given range of interest. • The polarized magnets of the nuclei begin to spin together, creating a radio frequency (RF) that is observable. Because the signals decays over time, this time-dependent pattern can be converted into a frequency-dependent pattern of nuclear resonances using a mathematical function known as a Fourier transformation, revealing the nuclear magnetic resonance spectrum. • The use of pulses of different shapes, frequencies and durations in specifically-designed patterns or pulse sequences allows the spectroscopist to extract many different types of information about the molecule. Nuclear Magnetic Resonance (NMR) • Time intervals between pulses allow—among other things— magnetization transfer between nuclei and, therefore, the detection of the kinds of nuclear-nuclear interactions that allowed for the magnetization transfer. • Interactions that can be detected are usually classified into two kinds. There are through-bond interactions and through-space interactions. The latter is a consequence of the so-called nuclear Overhauser effect (NOE). Measured NOEs lead to a set of distances between atoms. • These distances are subjected to a technique called Distance Geometry which normally results in an ensemble of possible structures that are all relatively consistent with the observed distance restraints (NOEs). • Richard Ernst and Kurt Wüthrich —in addition to many others— developed 2-dimensional and multidimensional FT-NMR into a powerful technique for the determination of the structure of biopolymers such as proteins or even small nucleic acids. • This is used in protein nuclear magnetic resonance spectroscopy. Wüthrich shared the 2002 Nobel Prize in Chemistry for this work. 2D NOESY spectrum Gly Val Gly Leu Ser Thr Phe Asp Asn Asp • Peptide sequence (N-terminal NH not observed) • Arg-Gly-Asp-Val-Asn-Ser-Leu-Phe-Asp-Thr-Gly NMR structure determination: hen lysozyme • 129 residues – ~1000 heavy atoms – ~800 protons 1.2 104 • NMR data set • 80 structures calculated • 30 low energy structures used 4 8000 Total energy – 1632 distance restraints – 110 torsion restraints – 60 H-bond restraints 1 10 6000 4000 2000 0 10 20 30 40 50 Structure number 60 70 Solution Structure Ensemble • Disorder in NMR ensemble – lack of data ? – or protein dynamics ? Problems with NMR • Protein concentration in sample needs to be high (multimilligram samples) • Restricted to smaller sized proteins (although magnets get stronger, 800 MHz, 900 MHz, even 1100 MHz). • Uncertainties in NOEs introduced by internal motions in molecules (preceding slide) X-ray and NMR summary • Are experimental techniques to solve protein structures (although they both need a lot of computation) • Nowadays typically contain many refinement and energy-minimisation steps to optimise the structure (next topic) X-ray and NMR summary (Cntd.) • X-ray diffraction – From crystallised protein sample to electron density map • Structure descriptors: resolution, R-factor, B-factor • Nuclear magnetic resonance (NMR) – Based on atomic nuclear spin – Produces set of distances between residues (distance restraints) – Distances are used to build protein model using Distance Geometry (a technique to build a protein structure using a set of inter-residue distances) Protein binding and protein-protein interactions • Complexity: – Multibody interaction • Diversity: – Various interaction types • Specificity: – Complementarity in shape and binding properties Protein-protein interactions • Many proteins interact through hydrophobic patches • Hydrophobic patches often have a hydrophilic rim • The patch-rim combination is believed to be important in providing binding specificity hydrophilic hydrophobic very hydrophilic PPI Characteristics • Universal – Cell functionality based on protein-protein interactions • Cyto-skeleton • Ribosome • RNA polymerase • Numerous – Yeast: • ~6.000 proteins • at least 3 interactions each ~18.000 interactions – Human: • estimated ~100.000 interactions • Network – simplest: homodimer (two identical domains interact) – common: hetero-oligomer (more) – holistic: protein network (all) • Contact area Interface Area – usually >1100 Å2 – each partner >550 Å2 • each partner loses ~800 Å2 of solvent accessible surface area – ~20 amino acids lose ~40 Å2 – ~100-200 J per Å2 • Average buried accessible surface area: – 12% for dimers – 17% for trimers – 21% for tetramers • 83-84% of all interfaces are flat • Secondary structure: – – – – 50% -helix 20% -sheet 20% coil 10% mixed • Less hydrophobic than core, more hydrophobic than exterior Complexation Reaction • A + B AB – Ka = [AB]/[A]•[B] association – Kd = [A]•[B]/[AB] dissociation Experimental Methods for determining PPI • 2D (poly-acrylamide) gel electrophoresis mass spectrometry • Liquid chromatography – e.g. gel permeation chromatography • Binding study with one immobilized partner – e.g. surface plasmon resonance • In vivo by two-hybrid systems (yeast two-hybrid or Y2H), FRET or tanden affinity purification (TAP) • Binding constants by ultra-centrifugation, micro-calorimetry or competition • Experiments with labelled ligand – e.g. fluorescence, radioactivity • Role of individual amino acids by site directed mutagenesis • Structural studies – e.g. NMR or X-ray PPI Network http://www.phy.auckland.ac.nz/staff/prw/biocomplexity/protein_network.htm Some terminology • Transient interactions: – Associate and dissociate in vivo • Weak transient: – dynamic oligomeric equilibrium • Strong transient: – require a molecular trigger to shift the equilibrium • Obligate PPI: – protomers no stable structures on their own (i.e. they need to interact in complexes) – (functionally obligate) Analysis of 122 Homodimers • 70 interfaces single patched • 35 have two patches • 17 have three or more Interfaces • ~30% polar • ~70% non-polar Interface • Rim is water accessible rim interface Some amino acid preferences prefer avoid Ribosomal 70S structure at 5.5 Å (Noller et al. Science 2001) Calculating interface areas Given a complex AB: 1. Calculate Solvent Accesible Surface Area (ASA) of A, of B, and of AB 1. ASA lost upon complex formation is ASA(A)+ASA(B)-ASA(AB) 3. Interface area of A and of B is (ASA(A)+ASA(B)-ASA(AB))/2 Docking: predicting binding sites with ZDOCK • Protein-protein docking – 3-dimensional (3D) structure of protein complex – starting from 3D structures of receptor and ligand • Rigid-body docking algorithm (ZDOCK) – pairwise shape complementarity function – all possible binding modes – using Fast Fourier Transform algorithm • Refinement algorithm (RDOCK) – Take top 2000 predicted structures from ZDOCK (RDOCK is too computer intensive to refine very many possible dockings) – three-stage energy minimization – electrostatic and desolvation energies • molecular mechanical software (CHARMM) • statistical energy method (Atomic Contact Energy) • Example: 49 non-redundant unbound test cases: – near-native structure (<2.5Å) on top for 37% test cases • for 49% within top 4 Protein-protein docking • Finding correct surface match • Systematic search: – 2 times 3D space! • Define functions: – ‘1’ on surface – ‘r’ or ‘d’ inside – ‘0’ outside d r Docking Programs • • • • • • • • • • • • • • ZDOCK, RDOCK AutoDock Bielefeld Protein Docking DOCK DOT FTDock, RPScore and MultiDock GRAMM Hex 3.0 ICM Protein-Protein docking (Abagyan group, currently the best) KORDO MolFit MPI Protein Docking Nussinov-Wolfson Structural Bioinformatics Group … Docking Programs Issues: • Rigid structures or made flexible? – Side-chains – Main-chains • Full atomic detail or simplified models? • Docking energy functions (purpose built force fields) Summary protein(-protein) interactions • Different binding modes (transient, obligate, also depending on (co)localisation, etc.) • Hydrophobic patch/hydrophilic rim conferring binding specificity • Interfaces are physico-chemically positioned in between surface and protein core (amino acid composition, etc.) • Many approaches exist to computationally predict binding sites and therefore PPI Protein motion 1. For protein function, architecture and dynamics are both essential 2. Protein are very mobile and flexible objects 3. Energy measurements upon protein folding show that most proteins are marginally stable Molecular motions Proteins are very dynamic systems • Protein folding • Protein structure • Protein function (e.g. opening and closing of oxygen binding site in hemoglobin) Protein motion • Principles • Simulation – MD – MC The Ramachandran plot Allowed phi-psi angles Red areas are preferred, yellow areas are allowed, and white is avoided Molecular mechanics techniques Two basic techniques: • Molecular Dynamics (MD) simulations • Monte Carlo (MC) techniques Molecular Dynamics (MD) simulation • MD simulation can be used to study protein motions. It is often used to refine experimentally determined protein structures. • It is generally not used to predict structure from sequence or to model the protein folding pathway. MD simulation can fold extended sequences to `global' potential energy minima for very small systems (peptides of length ten, or so, in vacuum), but it is most commonly used to simulate the dynamics of known structures. • Principle: an initial velocity is assigned to each atom, and Newton's laws are applied at the atomic level to propagate the system's motion through time • MD simulation incorporates a notion of time K = kinetic energy V = potential energy q = coordinates p = momentum Molecular Dynamics Knowledge of the atomic forces and masses can be used to solve the position of each atom along a series of extremely small time steps (on the order of femtoseconds = 10-15 seconds). The resulting series of snapshots of structural changes over time is called a trajectory. The use of this method to compute trajectories can be more easily seen when Newton's equation is expressed in the following form: v = dri/dt a = d2ri/d2t The "leapfrog" method is a common numerical approach to calculating trajectories based on Newton's equation. This method gets its name from the way in which positions (r) and velocities (v) are calculated in an alternating sequence, `leaping' past each other in time The steps can be summarized as follows: Force field The potential energy of a system can be expressed as a sum of valence (or bond), crossterm, and nonbond interactions: The energy of valence interactions comprises bond stretching (Ebond), valence angle bending (Eangle), dihedral angle torsion (Etorsion), and inversion (also called out-ofplane interactions) (Einversion or Eoop) terms, which are part of nearly all force fields for covalent systems. A Urey-Bradley term (EUB) may be used to account for interactions between atom pairs involved in 1-3 configurations (i.e., atoms bound to a common atom): Evalence = Ebond + Eangle + Etorsion + Eoop + EUB Modern (second-generation) forcefields include cross terms to account for such factors as bond or angle distortions caused by nearby atoms. Cross terms can include the following terms: stretch-stretch, stretch-bend-stretch, bend-bend, torsion-stretch, torsion-bend-bend, bend-torsion-bend, stretch-torsion-stretch. The energy of interactions between nonbonded atoms is accounted for by van der Waals (EvdW), electrostatic (ECoulomb), and (in some older forcefields) hydrogen bond (Ehbond) terms: Enonbond = EvdW + ECoulomb + Ehbond Force field energy f= distance a/r12 - b/r6 Van der Waals forces The Lennard-Jones potential is mildly attractive as two uncharged molecules or atoms approach one another from a distance, but strongly repulsive when they approach too close. The resulting potential is shown (in pink). At equilibrium, the pair of atoms or molecules tend to go toward a separation corresponding to the minimum of the Lennard--Jones potential (a separation of 0.38 nanometers for the case shown in the Figure) Thermal bath Figure: Snapshots of ubiquitin pulling with constant velocity at three different time steps. Docking example: antibody HyHEL-63 (cyan) complexed with Hen Egg White Lysozyme (yellow) Important for binding is a salt bridge (i.e. charge complementary interaction) between Lys97 of HEL and Asp27 of the antibody heavy chain, as demonstrated by Molecular Dynamics (MD) The X-ray structure of the antibody HyHEL-63 (cyan) uncomplexed and complexed with Hen Egg White Lysozyme (yellow) has shown that there are small but significant, local conformational changes in the antibody paratope on binding. The structure also reveals that most of the charged epitope residues face the antibody. Details are in Li YL, Li HM, Smith-Gill SJ and Mariuzza RA (2000) The conformations of the X-ray structure Three-dimensional structures of the free and antigen-bound Fab from monoclonal antilysozyme antibody HyHEL-63. Biochemistry 39: 6296-6309. Salt links and electrostatic interactions provide much of the free energy of binding. Most of the charged residues face in interface in the X-ray structure. The importance of the salt link between Lys97 of HEL and Asp27 of the antibody heavy chain is revealed by molecular dynamics simulations. After 1NSec of MD simulation at 100°C the overall conformation of the complex has changed, but the salt link persists. Details are described in Sinha N and Smith-Gill SJ (2002) Electrostatics in protein binding and function. Current Protein & Peptide Science 3: 601-614. Monte Carlo (MC) simulation • "Monte Carlo Simulation" is a term for a general class of optimization methods that use randomization. • The general idea is, given the current configuration and some figure of merit, e.g., the energy of the folded configuration, to generate a new configuration at random (or semi-random): If the energy of the new configuration is smaller than the old configuration, always accept it as the next configuration; if it is worse than the current configuration, accept or reject it it with some probability dependent on how much larger the new energy is than the old energy. E = E(new)-E(old) If E<0 then accept else if random[0, 1] < e-E /kT then accept P E else reject Boltzmann -- probability of conformation c: P(c) = e-E(c)/kT Monte Carlo (MC) simulation • The idea is that by always accepting a better configuration, on the average the system will tend to move toward a (local) energy minimum, while conversely, by sometimes accepting worse configurations, the system will be able to "climb" out of a sub-optimal local minima, and perhaps fall into the basin of attraction of the global minimum. Local minimum Global minimum E Configuration space (models) • The specific algorithms for probabilistically generating and accepting new configurations define the type of "Monte Carlo" algorithm; some common methods are "Metropolis," "Gibbs Sampler," "Heat Bath," "Simulated Annealing," "Great Deluge," etc. • MC techniques are computationally more efficient than MD • MC simulations do not incorporate a notion of time! #! /usr/bin/perl #=============================================================================== # # $Id: mcdemo.pl,v 1.1.1.1 2003/03/12 16:13:28 jkleinj Exp $ # # mcdemo: Demo program for MC simulation of the number pi # # (C) 2003 Jens Kleinjung # # Dr Jens Kleinjung, Room P440 | [email protected] # Bioinformatics Unit, Faculty of Sciences | Tel +31-20-444-7783 # Free University Amsterdam | Fax +31-20-444-7653 # De Boelelaan 1081A, 1081 HV Amsterdam | http://www.cs.vu.nl/~jkleinj # #=============================================================================== # preset parameters $hits = 1; $miss = 1; for ($i=0; $i<100000; $i++) { # assign random x,y coordinates $x = rand; $y = rand; # calculate radius $r = sqrt(($x*$x)+($y*$y)); # sum up hits and misses if ($r <= 1) { $hits++; } else { $miss++; } # calculate pi $pi = (4*$hits)/($hits +$miss); # print pi if ($i%100 == 0) { print("$i $pi\n"); } } #=============================================================================== In many conformational search methods based on Monte Carlo (MC), after a MC move, the system is energy minimised, i.e. put in the lowest local energy conformation, for example by gradient descent (steepest descent). What can be done with MD and MC Dynamics of proteins • Protein folding – very difficult • Protein unfolding – done with MD • Structure refinement – most frequent application – After experimental structure elucidation – After some model building operation • PPI – Interaction dynamics, Docking • Hydrophobic patch dynamics Take home messages • Experimentally determining protein structures – X-ray diffraction • From crystallised protein sample to electron density map – Structure descriptors: resolution, R-factor – Nuclear magnetic resonance (NMR) • Based on atomic nuclear spin • Produces set of distances between residues (distance restraints) • Distances are used to build protein model using Distance Geometry • Protein dynamics simulation – Molecular dynamics • Follows Newton’s equations of motion • Simulates molecular movements through time • Very small time steps (typically 2 femtoseconds = 2*10-15 seconds) • Protein conformational search – Monte Carlo • Conformations are randomly changed • Uses Mitropolis criterion to decide between conformation i and i+1 based on conformational internal energy and the Boltzmann equation • Has no notion of time, is a conformational search protocol – Normally faster than MD so more conformations can be generated