Download Document

A Macroeconomic Model
with a Financial Sector
Markus K. Brunnermeier and Yuliy Sannikov
Motivation
• Current financial turmoil
– Spirals and adverse feedback loops
– Spillovers
• Across financial institutions
• To real economy
• Current macro approach
– Representative agent analysis ignores
• wealth distribution (including leveraged lending)
• spillovers (externalities) and hence,
• financial stability
– Steady-state log-linearization ignore many dynamic
effects (like precautionary hoarding due to higher volatility).
3
Modeling financial frictions
• Central idea: heterogeneous agents
• have special skills/more productive
Bernanke-Gertler-Gilchrist, He-Krishnamurthy, Kiyotaki-Moore
• less risk-averse  Geanakoplos, Adrian-Shin, Garleanu-Pedersen
• more optimistic  Geanakoplos
type 1: financially constrained
type 2: unlevered
4
Modeling financial frictions
• Central idea: heterogeneous agents
• have special skills/more productive
Bernanke-Gertler-Gilchrist, He-Krishnamurthy, Kiyotaki-Moore
• less risk-averse  Geanakoplos, Adrian-Shin, Garleanu-Pedersen
• more optimistic  Geanakoplos
type 1: financially constrained
capital
capital
financing
inside
equity
financing
inside
equity
type 2: unlevered
type 3: intermediary
Debt
Equity
Diamond (1984)
5
Modeling financial frictions
• Central idea: heterogeneous agents
• have special skills/more productive
Bernanke-Gertler-Gilchrist, He-Krishnamurthy, Kiyotaki-Moore
• less risk-averse  Geanakoplos, Adrian-Shin, Garleanu-Pedersen
• more optimistic  Geanakoplos
type 1: financially constrained
type 2: unlevered
• Amplification (e.g. Brunnermeier-Pedersen)
•
Shocks affect the distribution
of assets between agents of
types 1 and 2, total output
Fire
sales
shock
to net
worth
Loss of Precaution
+ tighter
capital
margins
volatility
price 
6
Modeling financial frictions
• Central idea: heterogeneous agents
• have special skills/more productive
Bernanke-Gertler-Gilchrist, He-Krishnamurthy, Kiyotaki-Moore
• less risk-averse  Geanakoplos, Adrian-Shin, Garleanu-Pedersen
• more optimistic  Geanakoplos
type 1: financially constrained
type 2: unlevered
• Amplification (e.g. Brunnermeier-Pedersen)
Fire
sales
•
Shocks affect the distribution
of assets between agents of
types 1 and 2, total output
But…
shock
to net
worth
Existing models study only
steady-state dynamics or local dynamics
two-three period models
Loss of Precaution
+ tighter
capital
margins
volatility
price 
7
Preview of results
1. Unified model, replicates dynamics near steady state (e.g.
Bernanke-Gertler-Gilchrist)
prices
expert net worth
volatility
… but unstable dynamics away from steady state
due to (nonlinear) liquidity spirals
2. Welfare: Fire-sale externalities within financial sector,
externalities b/w financial sector and real economy…
–
–
When levering up, institutions ignore that their fire-sales depress
prices for others
Inefficient pecuniary externality in incomplete market setting
3. Securitization can lead to excessive leverage
Overview
• Start with simple model
• Show non-linearities in equilibrium
• Add households, capital producers and direct
investment to show externalities
• Add idiosyncratic shocks to show effects of
securitization
9
Model: production of output and capital
• Experts hold capital, which produces output
yt = a k t
• Investment of ι(g) kt makes capital grow at rate g
• δ: expert depreciation
ι(-δ) = 0
• Liquidation value:
ι’(-∞) = a/(r + δ*), δ* > δ
Household discount rate
Household depreciation
10
Model: production of output and capital
• Experts hold capital, which produces output
yt = a k t
• Investment of ι(g) kt makes capital grow at rate g
• δ: expert depreciation
ι(-δ) = 0
• Liquidation value:
ι’(-∞) = a/(r + δ*), δ* > δ
Household discount rate
• Holding capital is risky
Household depreciation
Brownian
macro shock
dkt = g kt dt +  kt dZt
• ρ ≥ r: expert discount rate (may “pay out” too much)
11
Financing through experts
• Agency problem: experts can increase depreciation/cause losses
• Get benefit b per unit of capital
Assets
Liabilities
Experts
borrow and
may unload
some risk
dt = ktipt – et
ktipt
Inside
nt = αtet
Outside
(1-αt)et
et
– Assume: effort, kti not contractible, but market value of assets ptkti is
– Incentive constraint
b - t pt ≤ 0 
t  b/pt
- Solvency constraint: debt holders liquidate when ktpt drops to dt
- Expert capital depends on aggregate risk, amplified through prices
- Later: contracting on aggregate risk separately
12
Balance sheets
• For simplicity, take α = 1 for most of this talk
Assets
ptkt
Liabilities
Debt dt
dpt= tp dt+tp dZt
dkt = gkt dt+kt dZt
Equity =
net worth
nt = ptkt - dt
d(ktpt) = kt (g pt + tp + tp) dt + kt (pt + tp) dZt
ddt = (r dt - a kt + ι(g) kt) dt - dct
13
Evolution of balance sheets
– Asset side – long maturity
d(ktpt) = kt (g pt + tp + tp)dt + kt (pt + tp)dZt
– Liability side
1. Debt – overnight maturity
ddt = (r dt - a kt + ι(g) kt) dt - dct
2. Equity
dnt = d(ktpt) - ddt =
rnt + kt [(a-ι(g)-(r-g)pt+tp+tp)dt+(pt+tp)dZt] -dct
14
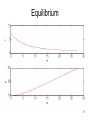
Equilibrium
•
•
•
•
•
Aggregate: Nt, Kt
State variable t = Nt/Kt
Price p(t)
Expert value function f(t)nt
Bellman equation
f(t)nt = maxk,g,c E[dc+d(f(t)nt)] = maxk,g,c
{dct+μtfnt + f(t) (rnt + kt(a-ι(g)-(r-g)pt+tp+tp)) + σtfkt(pt+tp)}
FOC: ι’(g) = pt,
a-ι(g)-(r-g)pt+tp+tp = - σtf/f(t) (pt+tp)
dct = 0 unless f(t)=1
(risk premium) * pt
Bellman equation: ( - r) f(t) =μtf
15
Ito’s lemma: tp = tη p’ + ½(tη)2p’’  differential equations
Stochastic Discount Factor
• Experts’ SDF:
m0,t = e-ρt
f(ηt)/f(η0)
time preference agency constraint
• Households’ SDF: m0,tHH= e-rt
– Note that m0,t =/ m0,tHH, since δ*> δ
Equilibrium
17
Equilibrium
18
Full vs. steady-state dynamics
•
Log-linearized impulse response functions
prices
expert net worth
volatility
time
•
Stationary distribution around steady-state
ηt
•
•
But.. below steady state system gets unstable, volatility 
Liquidity spiral
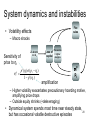
System dynamics and instabilities
Fire
sales
• Volatility effects
– Macro shocks
Sensitivity of
price to ηt
 tp 
Zt-shock
on kt
p' (t ) ( pt  t )
.
1  p' (t )
Loss of
capital
Precaution
+ tighter
margins
tp
pt
amplification
– Higher volatility exacerbates precautionary hoarding motive,
amplifying price drops
– Outside equity shrinks (+deleveraging)
• Dynamical system spends most time near steady state, 20
but has occasional volatile destructive episodes
Asset pricing (time-series)
• Predictability
– For low η values price is (temporarily) depressed
– Price-earnings ratio predicts future prices
• Current earnings: ak0
• Current price:
p0k0 =E0[e-ρt f(ηt)/f(η0) (ptkt+divt)]
• Excess volatility
– Volatility of ktpt per dollar is σ + σtp/pt
– Cash flow volatility amplified by SDF movements
• Stochastic volatility
– See ση plot
Asset pricing (cross section)
• Correlation increases with σp
– Extend model to many types j of capital
dkj/kj = g dt + σ dz + σ' dzj
aggregate uncorrelated
shock
shock
– Experts hold diversified portfolios
• Equilibrium looks as before, but
• Volatility of ptkt is σ + σp + σ’
• For uncorrelated zj and zl
correlation (ptjktj, ptlktl) is (σ + σp)/(σ + σp + σ’)
which is increasing in σp
Externalities
so far there are no externalities…
Proposition. The competitive equilibrium in this economy
is equivalent to the optimal policy by a monopolist
expert.
Sketch of proof. (1) Write Bellman equation for
monopolist. (2) Define price pt = ι’(g). (3) Show that
prices etc. are as in competitive eq.
Intuition: In competitive equilibrium experts do affect
prices by their choices (compensation and investment),
but they are isolated from prices because they don’t
trade given equilibrium prices.
23
Optimal payout policy of monopolist
Debt dDt = (rDt - a Kt + ι(g) Kt) dt – dCt, take ρ > r
Solvency constraint:
Dt ≤ LKt
Value function h(ωt)Kt where ωt = -Dt/Kt
Bellman equation…
24
Modification 1: add labor sector
• Fixed labor supply L
• Production function
a’ Kt kt1- lt
Workers get wages wt =  a’ Kt L-1
Experts get ak = (1 - ) a’ L k
Worker welfare depends on Kt
Experts do not take that into account when choosing
leverage (investment and payout decisions)
• Household value function…
•
•
•
•
25
Externalities with households
26
Modification 2: speculative households
• So far fixed liquidation value at a/(r + δ*)… now
households can sell back to experts
– Break even for HH
financing cost
earnings
Capital gains/losses, E[d(ktpt)]
a- rpt - δ*pt + tp+ tp ≤ 0,
equality when experts hold fraction ψt < 1 of
assets
– depreciation rate is δ* > δ
– pt ≥ a/(r + δ*)
• In equilibrium households pick up assets when financial
sector suffers losses, i.e. ηt becomes small
• Fire sale externalities (within financial sector) – when
levering up, experts hurt prices that other experts can sell
to households in the event of a crisis
27
Equilibrium
when
households
provide
liquidity
support
28
Modification 3: Idiosyncratic losses
dkti = g kti dt +  kti dZt + kti dJti
Jti is an idiosyncratic compensated Poisson loss process,
recovery distribution F and intensity λ(σtp)
Vt = ktpt drops below Dt, costly state verification by debt
Review: costly state verification
• Developed by Townsend (1979), used in Diamond
(1984), Bernanke-Gertler-Gilchrist
• Time 0: principal provides funding I to agent
• Time 1: agent’s profit y ~ F[0, y*] is his private
information but principal can verify y at cost
• Optimal contract (with deterministic verification) is debt
with face value D: agent reports y truthfully and pays D if
y ≥ D, triggers default and pays y if y < D
• In our context: expert can cause losses (reduce Vt for
private benefit); debtholders verify if Vt falls below Dt
Modification 3: Idiosyncratic losses
dkti = g kti dt +  kti dZt + kti dJti
Jti is an idiosyncratic compensated Poisson loss process,
recovery distribution F and intensity λ(σtp)
V = ktpt drops below Dt, costly state verification by debt
• Debtholders’ loss rate
( p )V  ( VD  x)dF(x)
D
V
0
• Verification cost rate
Asset
D
V

 ( p )V  cxdF( x)
0



C ( VD )
• Leverage bounded not only by
precautionary motive, but also
the cost of borrowing
Liabilities
Dt = ktpt – Et
Vt = ktpt
Equity
Equilibrium
• Experts borrow at rate larger than r
• Rate depends on leverage, price volatility
• dt = diffusion process (without jumps) because
losses cancel out in aggregate
32
Securitization
• Experts can contract on shocks Z and L directly
among each other, contracting costs are zero
• In principle, good thing (avoid verification costs)
• Equilibrium
– experts fully hedge idiosyncratic risks
– experts hold their share (do not hedge) aggregate risk
Z, market price of risk depends on tf (pt + tp)
– with securitization, experts lever up more (as a
function of t) and pay themselves sooner
– financial system becomes less stable
33
Contracting
• Agency problem: experts can lower growth rate/cause losses
• Get benefit b per unit of capital
Assets
Liabilities
dt = ktipt – et
ktipt
Inside
nt = αtet
Outside
(1-αt)et
et
– Assume: effort, kti not contractible, but market value of assets ptkti is
– Incentive constraint
b - t pt ≤ 0 
t  b/pt
- Expert capital depends on aggregate risk, amplified through prices
- Contracting on aggregate risk separately: consider that in an
extension, but only within financial sector
34
Evolution of balance sheets
– Asset side – long maturity
d(ktpt) = kt (g pt + tp + tp)dt + kt (pt + tp)dZt
– Liability side
1. Debt – overnight maturity
2. Outside equity: 1-t
3. Inside equity
Capital appreciation, E[d(ktpt)]
dnt = nt + kt [(a -  pt +g pt + tp+ tp)dt
+ t (pt+tp) dZt]
All results (nonlinear dynamics, externalities,
excessive leverage under securitization)
hold in this expanded model
35
Conclusion
• Incorporate financial sector in macromodel
– Higher growth
– Exhibits instability
– due to non-linear liquidity spirals (away from steady
state)
• Leverage/payouts chosen without taking into
account externalities
– Towards households (labor provision)
– Within financial sector:
possible fire sales compromise others’ balance sheets
• Securitization avoids inefficiencies, but can increase
instabilities (higher leverage/payout rate)
36
To do list
• Introducing risk aversion
– Asset pricing implication – time-varying risk premia
– Time-varying risk-free interest rate
• Incorporating instabilities into general DSGE
model
• Optimal regulation
• Introducing money/assets with different liquidity
• Exploring maturity mismatch
37
Thank you! ☺
Differences to Bernanke-Gertler-Gilchrist
BGG
Brunnermeier-Sannikov
1. “small” aggregate shocks, loglinearization around steady state
1.
Focus on (large) aggregate shocks
(idiosyncratic shocks not essential),
explore nonlinearities using
Bellman equation
2.
Price dynamics driven by idiosyncratic
shocks and default risk
–
Higher state verification costs when
expert capital goes down
2.
3.
With small aggregate noise, expert
incentives to keep “dry powder”
(liquidity) are negligible
Asset price drops also due to fire
sales
3.
Expert’s rent depends on state t
Incentive to keep “dry powder”
(liquidity)
4.
Procyclical leverage: Experts
reduce position after drop in net
worth

Liquidity spirals
4.
Countercyclical leverage
–
Experts take on same position after
drop in net worth
–
Leverage increases after drop in networth
5.
Debt vs. Equity
6.
No fire-sale externality
5.
Securitization
(debt, inside + outside equity)
6.
Fire-sale externality
(rationale for regulation)
39
Differences to Kiyotaki-Moore
KM – (Kiyotaki version)
BruSan
1.
1.
Zero-prob. temporary shock
–
–
2.
Persistent (dynamic loss spiral)
Amplified through collateral
value
Non- vs. productive
(leveraged) sector
Dual role of durable asset
3.
1.
2.
4.
Exogenous contract
–
–
5.
Production
Collateral
One period contract
Debt is limited by collateral
value
Durable asset doesn’t
depreciates (capital, fully)
Permanent TFP shocks


Investment through leveraged
financial sector
Dual role of durable asset
2.
3.
1.
2.
Production
Securitization
Optimal contract
4.


5.
Margin/haircut spiral
(leverage)
Loss spiral
Dynamic contract
Debt is limited due
idiosyncratic risk and costly
state verification
δ-depreciation rate
40
40
Differences to He-Krishnamurthy
He-Krishnamurthy
1.
–
–
2.
–
3.
–
–
–
–
Endowment economy
GDP growth is exogenously fixed
No physical investment
No direct investment in risky asset by households
Limited participation model
Contracting
Only short-run relationship (t to t+dt)
Fraction of return, fee
Asset composition (risky vs. risk-free) is not
contractable
Non-effort lowers return by xdt
•
BruSan


Direct investments by all households
3.
Contracting





–
–
4.
5.
6.
GDP growth depends on net-wealth
Physical investment
2.
x is exogenous,not linked to fundamental
Private benefit from shirking
No benchmarking
Pricing Implications
–
When experts wealth declines, their market
power increases, and so does their fee
–
Price impact depends on assumption that
household have larger discount rate than experts
Procyclical Leverage
In H-K calibration paper
1.
No fee, households are rationed in their
investment
2.
As expert wealth approaches 0, interest rate can
go to –∞
3.
Heterogeneous labor income for newborns of lDt
4.
Non-log utility function
Production economy
1.
(Potential) long-run relationship
Fraction of return, fee, size of asset pool
Effort increases fundamental growth to
gdt
Monetary benefit from shirking
No benchmarking
Pricing Implication
4.

Price drop with state variable
Countercyclcial Leverage
5.


Entrepreneur take on same position after
drop in networth
Leverage increases after drop in networth
41
Graphs: leverage
42