* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Lecture 11 AC Circuits Frequency Response
Schmitt trigger wikipedia , lookup
Operational amplifier wikipedia , lookup
Standing wave ratio wikipedia , lookup
Crystal radio wikipedia , lookup
Immunity-aware programming wikipedia , lookup
Power MOSFET wikipedia , lookup
Integrated circuit wikipedia , lookup
Power electronics wikipedia , lookup
Superheterodyne receiver wikipedia , lookup
Surge protector wikipedia , lookup
Phase-locked loop wikipedia , lookup
Mathematics of radio engineering wikipedia , lookup
Audio crossover wikipedia , lookup
Mechanical filter wikipedia , lookup
Switched-mode power supply wikipedia , lookup
Resistive opto-isolator wikipedia , lookup
Distributed element filter wikipedia , lookup
Radio transmitter design wikipedia , lookup
Opto-isolator wikipedia , lookup
Wien bridge oscillator wikipedia , lookup
Equalization (audio) wikipedia , lookup
Analogue filter wikipedia , lookup
Valve RF amplifier wikipedia , lookup
Zobel network wikipedia , lookup
Rectiverter wikipedia , lookup
Regenerative circuit wikipedia , lookup
Index of electronics articles wikipedia , lookup
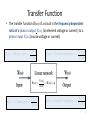
Lecture 11 AC Circuits Frequency Response Contents • • • • • Introduction Transfer Function Series Resonance Parallel Resonance Passive Filters 2 Introduction What is Frequency Response of a Circuit? It is the variation in a circuit’s behavior with change in signal frequency and may also be considered as the variation of the gain and phase with frequency. 3 Transfer Function • The transfer function H(ω) of a circuit is the frequency-dependent ratio of a phasor output Y(ω) (an element voltage or current ) to a phasor input X(ω) (source voltage or current). H( ) Voltage gain Vo ( ) Vi ( ) H( ) I ( ) H( ) Current gain o Ii ( ) H( ) Transfer Impedance Vo ( ) Ii ( ) Y( ) | H( ) | X( ) H( ) Transfer Admittance I o ( ) Vi ( ) 4 Transfer Function: Example Example 1 For the RC circuit shown below, obtain the transfer function Vo/Vs and its frequency response. Let vs = Vmcosωt. 5 Solution (Example 1) Solution: The transfer function is 1 V 1 jC H( ) o Vs R 1/ j C 1 j RC , The magnitude is The phase is H( ) tan 1 1 1 ( / o ) 2 o o 1/RC Low Pass Filter 6 Transfer Function: Example Example 2 Obtain the transfer function Vo/Vs of the RL circuit shown below, assuming vs = Vmcosωt. Sketch its frequency response. 7 Solution (Example 2) Solution: The transfer function is H( ) Vo j L 1 Vs R j L 1 R j L High Pass Filter The magnitude is H( ) , 1 1 ( o 2 ) The phase is 90 tan 1 o R/L o 8 Series Resonance Resonance is a condition in an RLC circuit in which the capacitive and inductive reactance are equal in magnitude, thereby resulting in purely resistive impedance. Resonance frequency: 1 rad/s LC 1 fo Hz 2 LC o 1 Z R j ω L ω C or 9 Series Resonance The features of series resonance: 1 Z R j ω L ω C The impedance is purely resistive, Z = R; • The supply voltage Vs and the current I are in phase, so, cos = 1; • The magnitude of the transfer function H(ω) = Z(ω) is minimum; • The inductor voltage and capacitor voltage can be much more than the source voltage. 10 Series Resonance Bandwidth B The frequency response of the resonance circuit current is Vm I | I | R 2 ( L 1 / C) 2 The average power absorbed by the RLC circuit is P( ) The highest power dissipated occurs at resonance: 1 Z R j ω L ω C 1 2 IR 2 1 Vm2 P(o ) 2 R 11 Series Resonance Half-power frequencies ω1 and ω2 are frequencies at which the dissipated power is half the maximum value: 1 (Vm / 2 ) 2 Vm2 P(1 ) P(2 ) 2 R 4R 1 Vm2 P(o ) 2 R Highest power The half-power frequencies can be obtained by setting Z equal to √ 2 R. 1 R R 1 ( )2 2L 2L LC Bandwidth B 2 R R 1 ( )2 2L 2L LC o 1 2 B 2 1 12 Series Resonance: Quality factor Q Peak energy stored in the circuit o L 1 Energy dissipated by the circuit R o CR in one period at resonance The relationship between the B, Q and ωo: B R o o2 CR L Q • The quality factor is the ratio of its resonant frequency to its bandwidth. • If the bandwidth is narrow, the quality factor of the resonant circuit must be high. • If the band of frequencies is wide, the quality factor must be low. 13 Series Resonance Example 3 A series-connected circuit has R = 4 Ω and L = 25 mH. a. Calculate the value of C that will produce a quality factor of 50. b. Find ω1 and ω2, and B. c. Determine the average power dissipated at ω = ωo, ω1, ω2. Take Vm= 100V. 14 Parallel Resonance It occurs when imaginary part of Y is zero 1 1 Y j ( C ) R L Resonance frequency: 1 1 o rad/s or f o Hz LC 2 LC 15 Summary of series and parallel resonance circuits: characteristic Series circuit ωo 1 LC 1 LC Q ωo L 1 or R ωo RC R or o RC o L B ω1, ω2 Q ≥ 10, ω1, ω2 Parallel circuit o o Q o 1 ( Q 1 2 ) o 2Q 2Q o B 2 o 1 ( 1 2 o ) 2Q 2Q o B 2 16 Parallel Resonance Example 4 Calculate the resonant frequency of the circuit in the figure shown below. Answer: 19 2.179 rad/s 2 17 Passive Filters • A filter is a circuit that is designed to pass signals with desired frequencies and reject or attenuate others. Low Pass High Pass • Passive filter consists of only passive element R, L and C. Band Pass • There are four types of filters. Band Stop 18 Passive Filters Example 5 For the circuit in the figure below, obtain the transfer function Vo(ω)/Vi(ω). Identify the type of filter the circuit represents and determine the corner frequency. Take R1=100W =R2 and L =2mH. Answer: 25 krad/s 19