* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download transformer
Pulse-width modulation wikipedia , lookup
Power over Ethernet wikipedia , lookup
Audio power wikipedia , lookup
Current source wikipedia , lookup
Variable-frequency drive wikipedia , lookup
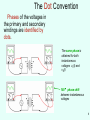
Power factor wikipedia , lookup
Power inverter wikipedia , lookup
Wireless power transfer wikipedia , lookup
Electric power transmission wikipedia , lookup
Stray voltage wikipedia , lookup
Single-wire earth return wikipedia , lookup
Electric power system wikipedia , lookup
Power MOSFET wikipedia , lookup
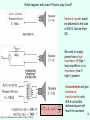
Electrification wikipedia , lookup
Voltage optimisation wikipedia , lookup
Opto-isolator wikipedia , lookup
Power electronics wikipedia , lookup
Buck converter wikipedia , lookup
Magnetic core wikipedia , lookup
Amtrak's 25 Hz traction power system wikipedia , lookup
Electrical substation wikipedia , lookup
Switched-mode power supply wikipedia , lookup
Transformer wikipedia , lookup
Mains electricity wikipedia , lookup
Power engineering wikipedia , lookup
Three-phase electric power wikipedia , lookup
Resonant inductive coupling wikipedia , lookup
ECE 3336 Introduction to Circuits & Electronics Set #16 Transformers Fall 2011, TUE&TH 4-5:30 pm Dr. Wanda Wosik 1 Inductors Inductors model the interaction between magnetic fields and voltage and current. df (t) v L (t) = N dt L= LX= #[H] iL + vL - diL vL = LX dt f (t)[Wb] i(t)[A] - Magnetic flux in webers [Wb] 2 Coupled Inductors • A current flowing in one inductor induces magnetic field that is felt by the second coil • If this field changes due to changes in the original current, the second coil will try to respond to eliminate these changes (the second coil wants to maintain the original magnetic field). • This occurs by producing a voltage in the second coil that would result in a current opposing these changes (through the magnetic field). Such interaction of both coils regarding their currents and voltages is referred to as mutual inductance. Such voltage generation that opposes the change in magnetic field will be a basis for transformers. Produces Constant Magnetic Field Produces Decreasing Magnetic Field Produces Increasing Magnetic Field Lenz’s law http://hyperphysics.phy-astr.gsu.edu/hbase/magnetic/indmut.html#c1 3 Mutual Inductance We model this effect with what we call “mutual inductance”, and we call it M [H] di1 v2 = M dt We also rename L [H], as the “self inductance” v1 = L Magnetomotive force di1 dt vp(t) vs(t) vp(t) vs(t) Voltage induced in v(t)=N•d/dt the secondary coil in response to current changes turns in the primary coil. Current direction = polarity important 4 http://www.allaboutcircuits.com/vol_2/chpt_9/7.html Mutual Inductance “Mutual inductance”, the influence of one coil on the other, is assumed in this course to be the same as the second on the first. That is, M12 = M21 = M. Sometimes we will use L11 and L22 for the self inductance and L12 and L21 for mutual inductance. di1 v1 = L dt We have i1 current in the primary coil di1 v2 = M dt We have i2 current in the secondary coil Remember that transformers will operate in AC conditions. The DC input voltage will not induce any voltage in the secondary winding (e.i. electrical isolation will give an isolation transformer). http://www.allaboutcircuits.com/vol_2/chpt_9/7.html 5 Ideal Transformers We can derive equations for voltage and current ratios in the ideal transformers both in the time domain and phasor domain time domain The same flux Hambley df (t) v1(t) = N1 dt df (t) v 2 (t) = N 2 dt Voltage and current ratios n2 V2 I1 N= = = . n1 V1 I2 n2 v2 i1 N= = = . n1 v1 i2 6 Dot Conventions for Ideal Transformers are both defined as the If v1 and v2 dotted terminal with respect to the undotted terminal, then n2 / n1 = v2 / v1 = N. If v1 and v2 are both defined as the undotted terminal with respect to the dotted terminal, then n2 v2 i1 N= = = . n1 v1 i2 n2 / n1 = v2 / v1 = N. Otherwise, n2 / n1 = -v2 / v1 = N. n2 V2 I1 N= = = . n1 V1 I2 7 The Dot Convention Phases of the voltages in the primary and secondary windings are identified by dots. The same phase is obtained for both instantaneous voltages v1(t) and v2(t) 180° phase shift between instantaneous voltages 8 Dot Conventions for Ideal Transformers Analogous relations are for currents: If i1 and i2 are both defined as entering the dotted terminal, then n2 / n1 = -i1 / i2 = N. n2 v2 i1 N= = = . n1 v1 i2 If i1 and i2 are both defined as leaving the dotted terminal, then n2 / n1 = -i1 / i2 = N. Otherwise, n2 / n1 = i1 / i2 = N. n2 V2 I1 N= = = . n1 V1 I2 9 Power in Ideal Transformers Note that if the voltage increases going from one side of a transformer to the other, the current decreases, and by the same factor. There is no power gain. The factor is the ratio of the number of turns. We named this as the turns ratio, N. ˜2 V * ˜ ˜ ˜ ˜ ˜ S1 = I V = NI = I2 V2 = S2 N * 1 1 * 2 We can tap the secondary voltage at two (or more) points n2 V2 I1 N= = = . n1 V1 I2 Center-tapped transformer 240 V 120V line 120V line 10 Examples of transformers Other configurations of transformers Center-tapped transformer Figure Power transformers 7.31, 7.32can be huge or small http://www.allaboutcircuits.com/vol_2/chpt_9/7.html 11 Impedance Reflection with Transformers Transformers can be used to match loads (impedances). Note that V2 V1 = , and I1 = I 2 N . N If we divide the first equation by the second, we get V1 V2 N = , or I1 I 2 2 Z2 N Z1 = Z 2 , or Z1 = 2 . N 2 12 Impedance Reflection with Transformers Transformers can be used to match loads (impedances). This means that if we look at the apparent impedance seen at the primary side of a transformer (Z’) we will see the impedance at the secondary side divided by the turns ratio squared. Z2 N Z1 = Z 2 , or Z1 = 2 . N 2 This can be very useful. It is often referred to as the reflected impedance. 13 The maximum power transfer in AC circuits Maximum power transfer to Rload (in DC) occurs when Rload=Rsource. In AC circuits we will need very similar impedance matching with the source: Zs=Rs+jXs 2) Now, from the complex power 1) The real power absorbed by Rload Z LVS VS* VS2 SL = V I = ´ = ZL Z S + Z L (Z S + Z L )* | Z S + Z L ) |2 PL = V˜L I˜L cosq = Re(V˜L I˜L ) Where: ZL V˜L = V˜S ZS + ZL ˜ ˜* V V * * S S I˜L = ( ) = Figure * ZS + ZL (Z S + Z7.35 L) Maximum power transfer if: ZL=ZS* RL=RS and XL=-XS * L L We calculate the real power (again) VS2 PL = Re(V I ) = Re( )Re(Z L ) | Z S + Z L |2 * L L VS2 = Re(Z L ) (RS + RL )2 + (X S + X L )2 = V RL (RS + RL )2 + (X S + X L )2 2 S PL=PLMAX 0 When will PLMAX? 14 Impedance transformation improves power delivery - example a) The heaters (62.5Ω and 15.625Ω) of 1,000W power rating operate in two circuits a) and b). b) If we use the heater a) with 125 V source the power will decrease P=250 W e.i. [(125V/62.5Ω)x125V] because I=2A Now if we use a step-up (N=2) transformer: the current delivered to Rload is again I=4A and the power is restored to P=1,000 W http://www.allaboutcircuits.com/vol_2/chpt_9/7.html V2 V1 = , and I1 = I 2 N . N 15 What happens with power? How to play it loud? Maximum power would be delivered to the load of 500 Ω. But we have 8Ω. AC Thevenin circuit We want to supply power from a high impedance (V high I low) amplifier to a low impedance (low V high I) speaker. N 2 Z1 = Z 2 , or Z1 = http://www.allaboutcircuits.com/vol_2/chpt_9/7.html Z2 . N2 A transformer will give impedance transformation ratio 500:8 so that the delivered power will reach its maximum 16 17 Electric power transmission (a) direct power transmission is affected by the line resistance Pload V˜load I˜load h= = Psource V˜source I˜source Rload = Rsource + Rline + Rload Figure 7.37a, b (b) power transmission with transformers 1 R''load = 2 (R'load +Rline ) = Rload + N 2 Rline N Reflected load here M=1/N R'load = 1 2 R = N Rload 2 load M What will be =? We will use impedance transformation for Figure 7.37a, b, Rizzoni 18 Electric power transmission - reduction of Rline by 1/N2 (c) equivalent circuit seen by generator R''load = (d) equivalent circuit seen by load R'source = N Rsource 2 Figure 7.37c, d h= 1 2 (R' +R ) = R + N Rline load line load 2 N Pload Rload = Psource Rsource + (1/N 2 )Rline + Rload 19 Figure 7.37c, d Balanced three-phase Power (AC circuit) Positive, or abc, sequence for balanced three-phase voltages (“-” acb) Wye-wye (Y-Y) connection neutral Line voltages ab, bc, ca Figure 7.40, 7.41 V˜ab = V˜an + V˜nb = V˜an - V˜bn V˜an = V˜bn = V˜cn = V˜ All line voltages Phase voltages V˜an = V˜anÐ0° V˜bn = V˜bnÐ(-120°) V˜cn = V˜cnÐ(-240°) = V˜cnÐ120° V˜ab = V˜Ð0° - V˜Ð(-120°) = 3V˜Ð30° V˜bc = V˜Ð(-120°) - V˜Ð(120°) = 3V˜Ð(-90°) V˜ca = V˜Ð120° - V˜Ð0° = 3V˜Ð150° Figure 7.41 Rizzoni V˜an + V˜bn + V˜cn = 0 20 Balanced three-phase AC circuit (redrawn) Three circuits are in parallel. I˜n = I˜a + I˜b + I˜c 1 ˜ (Van + V˜bn + V˜cn ) = 0 Z Can be eliminated V˜ pa (t) = (1+ cos2wt ) R V˜ pb (t) = [1+ cos(2wt - 120°)] R = Figure 7.42 V˜ pc (t) = [1+ cos(2wt + 120°)] R Advantage of the 3 phase also in less wiring (3) Compared to single phase (6 wires). Figure 7.42 p(t) = p a (t) + p b (t) + pc (t) 3V˜ 2 V˜ 2 = + [cos2wt + cos(2wt - 120°) R R 3V˜ 2 +cos(2wt + 120°)] = R Constant! power 21 Loads can be also in a delta connection Delta-connected generators Line (-to-line) voltage Figure 7.43 V=0 I=0 Currents drawn by wyeand by delta connected loads V˜ V˜ ˜ (Ian ) y = = Ð(-q ) Zy | Zy | For both currents to be the same we have to have Z=3Zy Rizzoni, Figure 7.43 Delta draws 3 times more current than a wye load does. 22 Line voltage convention for residential circuits A 3-wire AC system supplied by the power company red Higher line loss will be from the 120V source. To reduce power loss (I2R) thick wires are used. white (earth ground) black 83.3A Figure 7.50 Power loss=69.4 W Rs=0.02Ω 41.7.A V˜B - V˜R = V˜BR = V˜B - (-V˜B ) = 2V˜B = 240Ð0° Power loss=34.7 W This is the voltage (rms) between the hot wires 23 A typical residential wiring arrangement •Limit power dissipation by appropriate connections fro various loads. Figure 7.52 Figure 7.52 •Avoid heat generation (safety aspects) 24 Structure of an AC power distribution network (just for your curiosity) That reduces power losses in transmission lines Step-up transformer Figure Substations 7.58 An electric power network =the Power grid allows for redistribution of power to various substations (various V levels obtained after stepping-down). Your house is carefully wired! Figure 7.58 25