Download Student Lecture #1: Operational Amplifiers

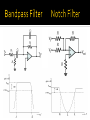
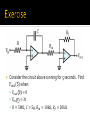
James Kelly
Nathan Knight
Gustavo Lee

Introduction

Characteristics of Ideal and Real Op-Amps

Basic Circuits of Op-Amps

Applications

Exercise



An Operational Amplifier (known as an “Op-Amp”) is an
integrated circuit that sets an output voltage based on the
input voltages provided.
In a circuit, it is used to perform an operation and an
amplification where the operation may be add, subtract,
filter, integrate, differentiate, etc.
Op-Amps are composed of transistors, resistors,
capacitors, and diodes.

1941: Karl Swartzel of Bell Labs developed the first Op-Amp.
 Used 3 vacuum tubes, only one input (inverting), and operated
on + 350 V to achieve 90 dB gain.

1947: Loebe Julie developed the Op-Amp as it is known today, with
two inputs – inverting and non-inverting.
 The differential input made a whole range of new functionality
possible.

1953: First commercially available Op-Amp.
 George A. Philbrick Researches (GAP-R). GAP-R pioneered the
first reasonable-cost, mass-produced operational amplifier

1961: Advent of solid-state, discrete Op-Amps.
 Made possible by the invention of the silicon transistor, which
led to the concept of Integrated Circuits (IC)
 Reduced power input to ±15V to ±10V

1962: Op-Amp in a potted module.
 Packaging in small black boxes allowed for integration with a
circuit

1963: First monolithic IC Op-Amp, the
μA702, designed by Bob Widlar at Fairchild
Semiconductor.


Monolithic ICs consist of a single chip
1968: Release of the μA741

The μA741 became the canonical Op-Amp, from
which many modern op-amps base their pinout
from, and is still in production today.
Parameter
Range
Frequency Spectrum
5-kHz to beyond 1-GHz GBW
Supply Voltage
0.9 V to a maximum 1000 V
Input Offsets
Approximately Zero

Introduction

Characteristics of Ideal and Real Op-Amps

Basic Circuits of Op-Amps

Applications

Exercise

𝑉𝑆+ : positive power supply

𝑉𝑆− : negative power supply

𝑉+ : non-inverting input terminal

𝑉− : inverting input terminal

𝑉𝑜𝑢𝑡 : output terminal
 𝑉+ , 𝑉− , 𝑉𝑜𝑢𝑡 are all referenced to ground
Parameter Name
Symbol
Value
Input impedance
𝑅𝑖𝑛
∞
Output impedance
𝑅𝑜𝑢𝑡
0
Open-loop gain
𝐺
∞
Bandwidth
𝐵
∞

Temperature-independent.
𝑉𝑜𝑢𝑡 = 𝐺 𝑉+ − 𝑉− = 𝐺 ∙ 𝑉𝑖𝑛

The maximum output voltage value is the supply voltage (saturation):
 𝑉𝑆− ≤ 𝑉𝑜𝑢𝑡 ≤ 𝑉𝑆+

What this means:
 Current flow into the op-amp from either input terminal is zero.
▪ 𝐼− = 𝐼+ = 0
 Differential voltage between the two input terminals is zero.
▪ 𝑉+ − 𝑉− = 0
Parameter Name
Symbol
Value
Input impedance
𝑅𝑖𝑛
106 Ω
Output impedance
𝑅𝑜𝑢𝑡
102 Ω
Open-loop gain
𝐺
104 ~107
Bandwidth
𝐵
103 ~109 Hz

Operating temperature range:
 Commercial: 0℃~70℃
 Industrial: −25℃~85℃
 Military: −55℃~125℃
𝑉𝑜𝑢𝑡 = 𝐺 𝑉+ − 𝑉− = 𝐺 ∙ 𝑉𝑖𝑛
Vout
Saturation results when the output
voltage is equal to the power supply’s
voltage
 In typical op-amps, the saturation level is
about 80% of the supply voltage.

Vsat+
Slope = G
Vin
Vsat-
Saturation
Cutoff Points

Positive Saturation Cutoff:
 𝑉𝑜𝑢𝑡 = 𝑉𝑠𝑎𝑡+ ≈ 𝑉𝑆+

Linear Mode:
 𝑉𝑜𝑢𝑡 = 𝐺 𝑉+ − 𝑉−

Negative Saturation Cutoff:
 𝑉𝑜𝑢𝑡 = 𝑉𝑠𝑎𝑡− ≈ 𝑉𝑆−

Introduction

Characteristics of Ideal and Real Op-Amps

Basic Circuits of Op-Amps

Applications

Exercise

A closed-loop op-amp has feedback from the
output back to one of the inputs, whereas an
open-loop op-amp does not.
Open-Loop
Closed-Loop

Negative feedback connects the output to the inverting
input (-), whereas positive feedback connects the output to
the non-inverting input (+).
Negative Feedback
Positive Feedback


Negative feedback op-amps can produce any voltage in the
supply power range.
Positive feedback op-amps can only produce the maximum
and minimum voltages of the range.
Vout
Vout
Vsat+
Vsat+
Vin
VsatNegative Feedback
Vin
VsatPositive Feedback

Functionality: to amplify the input voltage to output
voltage with a negative gain.
𝑉+ = 0 𝑉
 𝑉𝑖𝑛 = 𝑉− = 𝑅𝑖𝑛 ∙ 𝐼
 𝑉𝑜𝑢𝑡 = 𝑅𝑓 ∙ −𝐼



𝑉𝑜𝑢𝑡
𝑉𝑖𝑛
=
−𝐼∙𝑅𝑓
𝐼∙𝑅𝑖𝑛
𝑉𝑜𝑢𝑡 = −
𝑅𝑓
𝑅𝑖𝑛
∙ 𝑉𝑖𝑛
𝐼

Functionality: to amplify the input voltage to output
voltage with a positive gain.



𝑉𝑖𝑛 = 𝑉− = 𝑉+
𝑉− = 𝑅1 ∙ 𝐼
𝑉𝑜𝑢𝑡 = (𝑅1 + 𝑅2 ) ∙ 𝐼
𝑉𝑜𝑢𝑡

𝑉𝑖𝑛
𝐼∙(𝑅1 +𝑅2 )
=
𝐼∙𝑅1
𝑅2
 𝑉𝑜𝑢𝑡 = 1 +
𝑅1
∙ 𝑉𝑖𝑛
𝐼

Functionality: takes the summation of input voltages
over time and provides that as the output signal


𝑉+ = 0 𝑉
𝑉− 𝑡 = 𝑅 ∙ 𝐼(𝑡)= 𝑉𝑖𝑛 (𝑡)
𝑉𝑖𝑛 (𝑡)
 𝐼 𝑡 =
𝑅
𝑡
1
 𝑉𝑜𝑢𝑡 = − ∙
𝐼(𝜏)𝑑𝜏
0
𝐶
𝑡
1
 𝑉𝑜𝑢𝑡 = −
∙ 0 𝑉𝑖𝑛 (𝜏)𝑑𝜏
𝑅𝐶
𝐼(𝑡)

Functionality: takes the rate of change of the
inverted input voltage signal and provides that as
the output signal
𝑉+ = 0 𝑉
1
 𝑉− 𝑡 = 𝑉𝑖𝑛 (𝑡) = ∙ 𝐼 𝑡 𝑑𝑡

𝑑𝑉𝑖𝑛 (𝑡)
𝑑𝑡
𝐼 𝑡 =𝐶∙
 𝑉𝑜𝑢𝑡 = −𝑅 ∙ 𝐼(𝑡)


𝑉𝑜𝑢𝑡 = −𝑅𝐶 ∙
𝐶
𝑑𝑉𝑖𝑛 (𝑡)
𝑑𝑡

Functionality: takes the difference
between two signals and provides that
as the output
𝑉𝑜𝑢𝑡 =

If
𝑅𝑓
𝑅1
=
𝑅𝑔
𝑅2
𝑅𝑔
𝑅1
𝑅𝑔 +𝑅2
:
𝑉𝑜𝑢𝑡 =

𝑅1 +𝑅𝑓
𝑅𝑓
𝑅1
(𝑉2 −𝑉1 )
Moreover, if 𝑅𝑓 = 𝑅1 :
𝑉𝑜𝑢𝑡 = 𝑉2 − 𝑉1
𝑉2 −
𝑅𝑓
𝑉
𝑅1 1

Functionality: takes the sum of two or more input
voltages and provides an output voltage
proportional to the negative of the algebraic sum
𝑉𝑜𝑢𝑡 = −𝑅𝑓

+
𝑉2
𝑅2
+⋯+
𝑉𝑛
𝑅𝑛
If 𝑅1 = 𝑅2 = ⋯ = 𝑅𝑛 :
𝑉𝑜𝑢𝑡 = −

𝑉1
𝑅1
𝑅𝑓
𝑅1
(𝑉1 +𝑉2 + ⋯ + 𝑉𝑛 )
Moreover, if 𝑅𝑓 = 𝑅1 = 𝑅2 = ⋯ = 𝑅𝑛 :
𝑉𝑜𝑢𝑡 = −(𝑉1 +𝑉2 + ⋯ + 𝑉𝑛 )

By setting
𝑅𝑓
𝑅1
1
𝑛
= , the summing op-amp can be
used as an averaging operator:
1
𝑛
𝑉𝑜𝑢𝑡 = − (𝑉1 +𝑉2 + ⋯ + 𝑉𝑛 )

Introduction

Characteristics of Ideal and Real Op-Amps

Basic Circuits of Op-Amps

Applications

Exercise

Active filters
 Signal processing
 Digital Image processing


Strain gauges
Control circuits
 PID controllers for aircraft
 PI controllers for temperature measurement circuitry

And much more…


Attenuates frequencies above
the cutoff frequency.
Cutoff frequency (Hz):
 𝑓𝑐 =



1
2𝜋𝑅2 𝐶
Gain in the passband:
 𝐺=−
𝑅2
𝑅1
Attenuates frequencies below
the cutoff frequency.
Cutoff frequency (Hz):
 𝑓𝑐 =

1
2𝜋𝑅1 𝐶
Gain in the passband:
 𝐺=−
𝑅2
𝑅1
Strain gauges consist of a pattern
of resistive foil mounted on a
backing material.
 As the foil is subjected to stress,
the resistance of the foil changes in
a defined way.
 This results in an output signal
directly related to the stress value,
typically a few millivolts.
 Op-Amps are utilized to amplify
the output signal level to 5~10 V, a
suitable level for application to
data collection systems.


A proportional-integral-derivative (PID) controller is a generic feedback
mechanism widely used in industrial control systems.
 It calculates an “error” value as the difference between a measured process
variable and a desired setpoint.
 Using this error, it calculates a control input using tuning parameters 𝐾𝑝 , 𝐾𝑑 ,
and 𝐾𝑖 to drive the error to zero.
𝑡
𝑑
𝑢 𝑡 = 𝐾𝑝 𝑒 𝑡 + 𝐾𝑖
𝑒 𝜏 𝑑𝜏 + 𝐾𝑑 𝑒(𝑡)
𝑑𝑡
0

So where do op-amps come in?
 The error is calculated using a Summing Op-Amp.
 Using this error voltage:
▪ The derivative of the error is calculated using a Derivative Op-Amp.
▪ The integral of the error is calculated using an Inverting Op-Amp.
 The tuning parameters 𝐾𝑝 , 𝐾𝑑 , and 𝐾𝑖 can be selected by
appropriate selection of resistors and capacitors.


Comparators
Detectors
 Threshold detector
 Zero-level detector

Oscillators
 Wien bridge oscillator
 Relaxation oscillator

Level shifters

Introduction

Characteristics of Ideal and Real Op-Amps

Basic Circuits of Op-Amps

Applications

Exercise

Consider the circuit above running for 5 seconds. Find
𝑉𝑜𝑢𝑡 (5) when:
 𝑉𝑜𝑢𝑡 0 = 0
 𝑉𝑖𝑛 t = 3t
 𝑅 = 5𝑀Ω, 𝐶 = 5𝜇, 𝑅𝑖𝑛 = 10𝑘Ω, 𝑅𝑓 = 20𝑘Ω









Cetinkunt, Sabri. Mechatronics. Hoboken, NJ: John Wiley & Sons Inc., 2007.
Jung, Walter G. Op Amp Applications Handbook. Analog Devices, Inc., 2005.
“Operational Amplifier.” http://en.wikipedia.org/wiki/Operational_amplifier.
“Operational Amplifier Applications.”
http://en.wikipedia.org/wiki/Operational_amplifier_applications.
“The Strain Gauge.”
http://web.deu.edu.tr/mechatronics/TUR/strain_gauge.htm.
“The PID Controller.” http://en.wikipedia.org/wiki/PID_controller.
“Feedback in Electronic Circuits: An Introduction.”
http://ecee.colorado.edu/~ecen4827/lectures/dm_feedback1.pdf.
“Differentiator and Integrator Circuits”
http://www.allaboutcircuits.com/vol_3/chpt_8/11.html.
“Inverting Op-Amp” http://www.wiringdiagrams21.com/2009/12/17/basicinverting-op-amp-circuit-diagram/
 Questions?