* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Student Lecture #1: Operational Amplifiers
Signal-flow graph wikipedia , lookup
Three-phase electric power wikipedia , lookup
Dynamic range compression wikipedia , lookup
History of electric power transmission wikipedia , lookup
Electrical substation wikipedia , lookup
Audio power wikipedia , lookup
Scattering parameters wikipedia , lookup
Control theory wikipedia , lookup
PID controller wikipedia , lookup
Pulse-width modulation wikipedia , lookup
Immunity-aware programming wikipedia , lookup
Flip-flop (electronics) wikipedia , lookup
Power inverter wikipedia , lookup
Current source wikipedia , lookup
Variable-frequency drive wikipedia , lookup
Stray voltage wikipedia , lookup
Alternating current wikipedia , lookup
Analog-to-digital converter wikipedia , lookup
Control system wikipedia , lookup
Regenerative circuit wikipedia , lookup
Integrating ADC wikipedia , lookup
Two-port network wikipedia , lookup
Voltage optimisation wikipedia , lookup
Voltage regulator wikipedia , lookup
Buck converter wikipedia , lookup
Resistive opto-isolator wikipedia , lookup
Power electronics wikipedia , lookup
Wien bridge oscillator wikipedia , lookup
Mains electricity wikipedia , lookup
Switched-mode power supply wikipedia , lookup
Negative feedback wikipedia , lookup
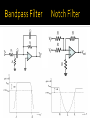
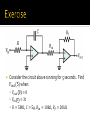
James Kelly Nathan Knight Gustavo Lee Introduction Characteristics of Ideal and Real Op-Amps Basic Circuits of Op-Amps Applications Exercise An Operational Amplifier (known as an “Op-Amp”) is an integrated circuit that sets an output voltage based on the input voltages provided. In a circuit, it is used to perform an operation and an amplification where the operation may be add, subtract, filter, integrate, differentiate, etc. Op-Amps are composed of transistors, resistors, capacitors, and diodes. 1941: Karl Swartzel of Bell Labs developed the first Op-Amp. Used 3 vacuum tubes, only one input (inverting), and operated on + 350 V to achieve 90 dB gain. 1947: Loebe Julie developed the Op-Amp as it is known today, with two inputs – inverting and non-inverting. The differential input made a whole range of new functionality possible. 1953: First commercially available Op-Amp. George A. Philbrick Researches (GAP-R). GAP-R pioneered the first reasonable-cost, mass-produced operational amplifier 1961: Advent of solid-state, discrete Op-Amps. Made possible by the invention of the silicon transistor, which led to the concept of Integrated Circuits (IC) Reduced power input to ±15V to ±10V 1962: Op-Amp in a potted module. Packaging in small black boxes allowed for integration with a circuit 1963: First monolithic IC Op-Amp, the μA702, designed by Bob Widlar at Fairchild Semiconductor. Monolithic ICs consist of a single chip 1968: Release of the μA741 The μA741 became the canonical Op-Amp, from which many modern op-amps base their pinout from, and is still in production today. Parameter Range Frequency Spectrum 5-kHz to beyond 1-GHz GBW Supply Voltage 0.9 V to a maximum 1000 V Input Offsets Approximately Zero Introduction Characteristics of Ideal and Real Op-Amps Basic Circuits of Op-Amps Applications Exercise 𝑉𝑆+ : positive power supply 𝑉𝑆− : negative power supply 𝑉+ : non-inverting input terminal 𝑉− : inverting input terminal 𝑉𝑜𝑢𝑡 : output terminal 𝑉+ , 𝑉− , 𝑉𝑜𝑢𝑡 are all referenced to ground Parameter Name Symbol Value Input impedance 𝑅𝑖𝑛 ∞ Output impedance 𝑅𝑜𝑢𝑡 0 Open-loop gain 𝐺 ∞ Bandwidth 𝐵 ∞ Temperature-independent. 𝑉𝑜𝑢𝑡 = 𝐺 𝑉+ − 𝑉− = 𝐺 ∙ 𝑉𝑖𝑛 The maximum output voltage value is the supply voltage (saturation): 𝑉𝑆− ≤ 𝑉𝑜𝑢𝑡 ≤ 𝑉𝑆+ What this means: Current flow into the op-amp from either input terminal is zero. ▪ 𝐼− = 𝐼+ = 0 Differential voltage between the two input terminals is zero. ▪ 𝑉+ − 𝑉− = 0 Parameter Name Symbol Value Input impedance 𝑅𝑖𝑛 106 Ω Output impedance 𝑅𝑜𝑢𝑡 102 Ω Open-loop gain 𝐺 104 ~107 Bandwidth 𝐵 103 ~109 Hz Operating temperature range: Commercial: 0℃~70℃ Industrial: −25℃~85℃ Military: −55℃~125℃ 𝑉𝑜𝑢𝑡 = 𝐺 𝑉+ − 𝑉− = 𝐺 ∙ 𝑉𝑖𝑛 Vout Saturation results when the output voltage is equal to the power supply’s voltage In typical op-amps, the saturation level is about 80% of the supply voltage. Vsat+ Slope = G Vin Vsat- Saturation Cutoff Points Positive Saturation Cutoff: 𝑉𝑜𝑢𝑡 = 𝑉𝑠𝑎𝑡+ ≈ 𝑉𝑆+ Linear Mode: 𝑉𝑜𝑢𝑡 = 𝐺 𝑉+ − 𝑉− Negative Saturation Cutoff: 𝑉𝑜𝑢𝑡 = 𝑉𝑠𝑎𝑡− ≈ 𝑉𝑆− Introduction Characteristics of Ideal and Real Op-Amps Basic Circuits of Op-Amps Applications Exercise A closed-loop op-amp has feedback from the output back to one of the inputs, whereas an open-loop op-amp does not. Open-Loop Closed-Loop Negative feedback connects the output to the inverting input (-), whereas positive feedback connects the output to the non-inverting input (+). Negative Feedback Positive Feedback Negative feedback op-amps can produce any voltage in the supply power range. Positive feedback op-amps can only produce the maximum and minimum voltages of the range. Vout Vout Vsat+ Vsat+ Vin VsatNegative Feedback Vin VsatPositive Feedback Functionality: to amplify the input voltage to output voltage with a negative gain. 𝑉+ = 0 𝑉 𝑉𝑖𝑛 = 𝑉− = 𝑅𝑖𝑛 ∙ 𝐼 𝑉𝑜𝑢𝑡 = 𝑅𝑓 ∙ −𝐼 𝑉𝑜𝑢𝑡 𝑉𝑖𝑛 = −𝐼∙𝑅𝑓 𝐼∙𝑅𝑖𝑛 𝑉𝑜𝑢𝑡 = − 𝑅𝑓 𝑅𝑖𝑛 ∙ 𝑉𝑖𝑛 𝐼 Functionality: to amplify the input voltage to output voltage with a positive gain. 𝑉𝑖𝑛 = 𝑉− = 𝑉+ 𝑉− = 𝑅1 ∙ 𝐼 𝑉𝑜𝑢𝑡 = (𝑅1 + 𝑅2 ) ∙ 𝐼 𝑉𝑜𝑢𝑡 𝑉𝑖𝑛 𝐼∙(𝑅1 +𝑅2 ) = 𝐼∙𝑅1 𝑅2 𝑉𝑜𝑢𝑡 = 1 + 𝑅1 ∙ 𝑉𝑖𝑛 𝐼 Functionality: takes the summation of input voltages over time and provides that as the output signal 𝑉+ = 0 𝑉 𝑉− 𝑡 = 𝑅 ∙ 𝐼(𝑡)= 𝑉𝑖𝑛 (𝑡) 𝑉𝑖𝑛 (𝑡) 𝐼 𝑡 = 𝑅 𝑡 1 𝑉𝑜𝑢𝑡 = − ∙ 𝐼(𝜏)𝑑𝜏 0 𝐶 𝑡 1 𝑉𝑜𝑢𝑡 = − ∙ 0 𝑉𝑖𝑛 (𝜏)𝑑𝜏 𝑅𝐶 𝐼(𝑡) Functionality: takes the rate of change of the inverted input voltage signal and provides that as the output signal 𝑉+ = 0 𝑉 1 𝑉− 𝑡 = 𝑉𝑖𝑛 (𝑡) = ∙ 𝐼 𝑡 𝑑𝑡 𝑑𝑉𝑖𝑛 (𝑡) 𝑑𝑡 𝐼 𝑡 =𝐶∙ 𝑉𝑜𝑢𝑡 = −𝑅 ∙ 𝐼(𝑡) 𝑉𝑜𝑢𝑡 = −𝑅𝐶 ∙ 𝐶 𝑑𝑉𝑖𝑛 (𝑡) 𝑑𝑡 Functionality: takes the difference between two signals and provides that as the output 𝑉𝑜𝑢𝑡 = If 𝑅𝑓 𝑅1 = 𝑅𝑔 𝑅2 𝑅𝑔 𝑅1 𝑅𝑔 +𝑅2 : 𝑉𝑜𝑢𝑡 = 𝑅1 +𝑅𝑓 𝑅𝑓 𝑅1 (𝑉2 −𝑉1 ) Moreover, if 𝑅𝑓 = 𝑅1 : 𝑉𝑜𝑢𝑡 = 𝑉2 − 𝑉1 𝑉2 − 𝑅𝑓 𝑉 𝑅1 1 Functionality: takes the sum of two or more input voltages and provides an output voltage proportional to the negative of the algebraic sum 𝑉𝑜𝑢𝑡 = −𝑅𝑓 + 𝑉2 𝑅2 +⋯+ 𝑉𝑛 𝑅𝑛 If 𝑅1 = 𝑅2 = ⋯ = 𝑅𝑛 : 𝑉𝑜𝑢𝑡 = − 𝑉1 𝑅1 𝑅𝑓 𝑅1 (𝑉1 +𝑉2 + ⋯ + 𝑉𝑛 ) Moreover, if 𝑅𝑓 = 𝑅1 = 𝑅2 = ⋯ = 𝑅𝑛 : 𝑉𝑜𝑢𝑡 = −(𝑉1 +𝑉2 + ⋯ + 𝑉𝑛 ) By setting 𝑅𝑓 𝑅1 1 𝑛 = , the summing op-amp can be used as an averaging operator: 1 𝑛 𝑉𝑜𝑢𝑡 = − (𝑉1 +𝑉2 + ⋯ + 𝑉𝑛 ) Introduction Characteristics of Ideal and Real Op-Amps Basic Circuits of Op-Amps Applications Exercise Active filters Signal processing Digital Image processing Strain gauges Control circuits PID controllers for aircraft PI controllers for temperature measurement circuitry And much more… Attenuates frequencies above the cutoff frequency. Cutoff frequency (Hz): 𝑓𝑐 = 1 2𝜋𝑅2 𝐶 Gain in the passband: 𝐺=− 𝑅2 𝑅1 Attenuates frequencies below the cutoff frequency. Cutoff frequency (Hz): 𝑓𝑐 = 1 2𝜋𝑅1 𝐶 Gain in the passband: 𝐺=− 𝑅2 𝑅1 Strain gauges consist of a pattern of resistive foil mounted on a backing material. As the foil is subjected to stress, the resistance of the foil changes in a defined way. This results in an output signal directly related to the stress value, typically a few millivolts. Op-Amps are utilized to amplify the output signal level to 5~10 V, a suitable level for application to data collection systems. A proportional-integral-derivative (PID) controller is a generic feedback mechanism widely used in industrial control systems. It calculates an “error” value as the difference between a measured process variable and a desired setpoint. Using this error, it calculates a control input using tuning parameters 𝐾𝑝 , 𝐾𝑑 , and 𝐾𝑖 to drive the error to zero. 𝑡 𝑑 𝑢 𝑡 = 𝐾𝑝 𝑒 𝑡 + 𝐾𝑖 𝑒 𝜏 𝑑𝜏 + 𝐾𝑑 𝑒(𝑡) 𝑑𝑡 0 So where do op-amps come in? The error is calculated using a Summing Op-Amp. Using this error voltage: ▪ The derivative of the error is calculated using a Derivative Op-Amp. ▪ The integral of the error is calculated using an Inverting Op-Amp. The tuning parameters 𝐾𝑝 , 𝐾𝑑 , and 𝐾𝑖 can be selected by appropriate selection of resistors and capacitors. Comparators Detectors Threshold detector Zero-level detector Oscillators Wien bridge oscillator Relaxation oscillator Level shifters Introduction Characteristics of Ideal and Real Op-Amps Basic Circuits of Op-Amps Applications Exercise Consider the circuit above running for 5 seconds. Find 𝑉𝑜𝑢𝑡 (5) when: 𝑉𝑜𝑢𝑡 0 = 0 𝑉𝑖𝑛 t = 3t 𝑅 = 5𝑀Ω, 𝐶 = 5𝜇, 𝑅𝑖𝑛 = 10𝑘Ω, 𝑅𝑓 = 20𝑘Ω Cetinkunt, Sabri. Mechatronics. Hoboken, NJ: John Wiley & Sons Inc., 2007. Jung, Walter G. Op Amp Applications Handbook. Analog Devices, Inc., 2005. “Operational Amplifier.” http://en.wikipedia.org/wiki/Operational_amplifier. “Operational Amplifier Applications.” http://en.wikipedia.org/wiki/Operational_amplifier_applications. “The Strain Gauge.” http://web.deu.edu.tr/mechatronics/TUR/strain_gauge.htm. “The PID Controller.” http://en.wikipedia.org/wiki/PID_controller. “Feedback in Electronic Circuits: An Introduction.” http://ecee.colorado.edu/~ecen4827/lectures/dm_feedback1.pdf. “Differentiator and Integrator Circuits” http://www.allaboutcircuits.com/vol_3/chpt_8/11.html. “Inverting Op-Amp” http://www.wiringdiagrams21.com/2009/12/17/basicinverting-op-amp-circuit-diagram/ Questions?