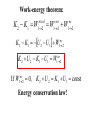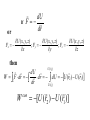Download y 1

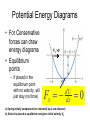
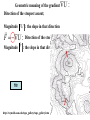
Nobel Prize in Physics 2008
Yoichiro Nambu
"for the discovery of the
mechanism of
spontaneous broken
symmetry in subatomic
physics"
Makoto Kobayashi Toshihide Maskawa
"for the discovery of the origin of the
broken symmetry which predicts the
existence of at least three families of quarks
in nature"
Broken Symmetries
The origin of mass
Higgs Mechanism:
A field fills all of space because of a
mechanism called spontaneous symmetry
breaking. It ‘sticks’ to particles, making it
‘harder for them to move’. This is what
gives quarks and leptons their mass.
Spontaneous symmetry breaking
Credit: CERN
As a consequence, there
should also be a spin-0
boson,2 the Higgs boson.
It has not been found yet.
Physics
Particles and Forces
Particle
Similar to the
celebrity effect
in a crowd.
H
The Standard Model
The Standard Model (SM) describes all these particles and 3 of 4
forces. We have confirmed the existence of those in the laboratory
experiments.
proton
+ Higgs boson
Higgs has not yet been discovered
The mass is constrained from LEP
and Tevatron data:
114 GeV<MH<154 GeV
Precision Cosmology at the LHC
3
SPUTNIK: spaceflight era begins
October 4, 1957
184-pound basketballsize satellite
Lasted 3 months
R-7 launcher: world’s first intercontinental ballistic missile
November 3, 1957: Sputnik 2, 1120 pounds
Laika
May 15, 1958: Sputnik 3, 1.5 tons
Total mass: 367 tons
Payload: about 1 ton
Thrust: 3.9x106 N
January 15, 1958: Explorer 1 launched (US)
April 12, 1961
Yuri Gagarin
February 20, 1962
John Glenn
Early timeline
April 12, 1961: the first human in space (Yuri Gagarin)
February 20, 1962: the first American on orbit (John Glenn)
1963: the first woman in space (Tereshkova)
1965: the first spacewalk (Leonov)
1969: first men on the moon (Collins, Armstrong, Aldrin)
1971: first space station (Salyut)
1981: first space shuttle flight (Columbia)
Robotic missions to all planets
Fathers of space programs
Sergei
Korolyov
1907-1966
Werner von Braun
1912-1977
Chapter 8
All forces are
CONSERVATIVE
or
NON-CONSERVATIVE
A force is conservative if:
The work
done
by the force in going


from r1 to r2 is independent of the path
the particle follows
or
The work done by the
 force when the
particle goes from r1 around a closed
path, back to r1 , is zero.
Non-conservative:
doesn’t
satisfy
above conditions
the
Theorem: if a force can be written as the gradient (slope)
of some scalar function, that force is conservative.
1D case:
dU
Fx  
dx
U(x) is called the  potential energy
function for the force F
If such a function exists, then the force is
conservative
x2
dU
Fx  
dx
W
W
con
x2
dU
  Fx dx   
dx
dx
x1
x1
 [U ( x2 )  U ( x1 )]
con
does NOT depend on path!
If Fx(x) is known, you can find the potential energy function as
U ( x)    Fx ( x) dx  C
Work-energy theorem:
K 2  K1  W
total
1 2
W
con
1 2
W
nc
1 2
K 2  K1  U 2  U1   W
nc
1 2
K 2  U 2  K1  U1  W
nc
12
nc
1 2
If W
 0, K 2  U 2  K1  U1  const
Energy conservation law!
A strategy: write down the total energy E = K + U at the
initial and final positions of a particle;
Then use
K 2  U 2  K1  U1 , if W
nc
1 2
or
K 2  U 2  K1  U1  W
nc
12
0
Examples
y
U ( y )  mgy  C
Force of gravity
Fy  mg
Fx  k ( x  x0 )
Spring force
x
k ( x  x0 )
U ( x) 
C
2
2
x0
A block of mass m is attached to a vertical spring,
spring constant k.
A
If the spring is compressed an amount A and the block
released from rest, how high will it go from its initial
position?
A particle is moving in one direction x and its potential
energy is given by U(x) = ax2 – bx4 .
Determine the force acting on a particle.
Find the equilibrium points where a particle can be at rest.
Determine whether these points correspond to a stable or
unstable equilibrium.
Potential Energy Diagrams
• For Conservative
forces can draw
energy diagrams
• Equilibrium
points
– If placed in the
equilibrium point
with no velocity, will
just stay (no force)
Fx >0
Fx  
dU
dx
a) Spring initially compressed (or stretched) by A and released;
b) A block is placed at equilibrium and given initial velocity V0
0
Stable vs. Unstable Equilibrium
Points
The force is zero at both maxima and minima
but…
– If I put a ball with no velocity there would it stay?
– What if it had a little bit of velocity?
Block of mass m has a massless spring connected to
the bottom. You release it from a given height H and
want to know how close the block will get to the floor.
The spring has spring constant k and natural length
L.
L
H
y=0
Several dimensions: U(x,y,z)
U ( x, y, z )
U ( x, y, z )
U ( x, y, z )
Fx  
; Fy  
; Fz  
x
y
z
Partial derivative is taken assuming all other arguments fixed
Compact notation using vector del, or nabla:

     
F  U ,   i 
j k
x
y
z

dU
Another notation: F   
dr
Geometric meaning of the gradient U
Direction of the steepest ascent;
Magnitude U : the slope in that direction

F  U : Direction of the steepest descent
Magnitude F : the slope in that direction
http://reynolds.asu.edu/topo_gallery/topo_gallery.htm
:
If
or

dU
F  
dr
U ( x, y, z )
U ( x, y, z )
U ( x, y, z )
Fx  
; Fy  
; Fz  
x
y
z
then

U ( r2 )
 


dU 
W   F  dr      dr    dU  U (r2 )  U (r1 )
L

dr
U ( r1 )
W
con


 [U (r2 )  U (r1 )]
H
Water Slide
Who hits the bottom with a faster speed?
Roller Coaster
You are in a roller coaster car of mass M that
starts at the top, height H, with an initial
speed V0=0. Assume no friction.
a) What is the speed at the bottom?
b) How high will it go again?
c) Would it go as high if there were friction?
H
Roller Coaster with Friction
A roller coaster of mass m starts at rest at height
y1 and falls down the path with friction, then
back up until it hits height y2 (y1 > y2).
Assuming we don’t know anything about the
friction or the path, how much work is done by
friction on this path?
A gun shoots a bullet at angle θ with the x axis
with a velocity of magnitude Vm. What is
magnitude of the velocity when the bullet
returns to the ground? How high it will go?
Power
Power is a rate at which a force does work
If work does not depend on time:
Otherwise:
W
P
t
 
W Fdr  
P

 Fv
dt
dt
Even if instantaneous power depends on time, one can
talk about the average power
Power could also define the rate at which any form
of energy is spent, not only mechanical
How many joules of energy does 100 watt light bulb use
per hour? How fast would a 70-kg person have to run to
have that amount of energy?