* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Gaining Momentum
Atomic theory wikipedia , lookup
Faster-than-light wikipedia , lookup
Hooke's law wikipedia , lookup
Hamiltonian mechanics wikipedia , lookup
Renormalization group wikipedia , lookup
Velocity-addition formula wikipedia , lookup
Relativistic quantum mechanics wikipedia , lookup
Tensor operator wikipedia , lookup
Monte Carlo methods for electron transport wikipedia , lookup
Symmetry in quantum mechanics wikipedia , lookup
Old quantum theory wikipedia , lookup
Routhian mechanics wikipedia , lookup
Uncertainty principle wikipedia , lookup
Centripetal force wikipedia , lookup
Center of mass wikipedia , lookup
Laplace–Runge–Lenz vector wikipedia , lookup
Rigid body dynamics wikipedia , lookup
Classical mechanics wikipedia , lookup
Quantum vacuum thruster wikipedia , lookup
Equations of motion wikipedia , lookup
Accretion disk wikipedia , lookup
Matter wave wikipedia , lookup
Work (physics) wikipedia , lookup
Theoretical and experimental justification for the Schrödinger equation wikipedia , lookup
Photon polarization wikipedia , lookup
Angular momentum wikipedia , lookup
Specific impulse wikipedia , lookup
Angular momentum operator wikipedia , lookup
Classical central-force problem wikipedia , lookup
Relativistic mechanics wikipedia , lookup
Relativistic angular momentum wikipedia , lookup
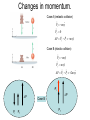
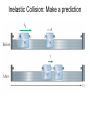
Gaining Momentum: Chapter 9 New Vocabulary: Linear Momentum P mV Impulse (force times time) Major Concepts of Chapter 9: •Linear momentum is conserved. It remains the same in the absence of an external force. •Linear momentum can be changed by an impulse (a force acting for a period of time). •Linear momentum is unchanged in collisions •There are two types of collisions: inelastic and elastic. Linear momentum is conserved in BOTH. •An “elastic” collision is one in which the objects “bounce”, and energy is conserved. •An “inelastic” collision is one in which the objects stick together, and energy is lost to heat. Why do we need momentum? • Momentum is useful because it remains unchanged in the absence of external forces • The total momentum of a system of moving objects is the sum of the individual momenta PTOT m1V1 m2V2 ... miVi i Note that momentum is a VECTOR. It has magnitude AND direction. Momentum changes with an external force. P F t Note: is for the case where mass is constant. This is a more accurate statement of Newton’s second law. An IMPULSE can cause a change in momentum. P Ft I Check the units: Momentum is mass X velocity = kg – m/s Impulse is mass X acceleration X time = kg-m/s^2 *s Newton’s Second Law Ptot Fext t mv t v m t ma Most general form. If mass is constant…. Constant mass form. Changes in momentum. Case A (inelastic collision) Pi mvyˆ Pf 0 P Pf Pi mvyˆ Case B (elastic collision) Pi mvyˆ Pf mvyˆ P Pf Pi 2mvyˆ -Pi P Pi Pf P Case B Pf Acting on Impulse: Change of Momentum Pi mvi xˆ Pf mv f xˆ P Pf Pi mv f vi xˆ P I FavgT Momentum Conservation • In the absence of an external force, linear momentum of a system of objects does not change. P I FavgT So, if the impulse (external force) is zero, The total momentum of a system of objects is the sum of the individual momenta. P Pf Pi 0 Pf Pi PTOT m1V1 m2V2 ... miVi i Elastic collision: make a prediction. We will do this experiment in a moment. Assume m1 = m2. If the initial speed is V, what are the final speeds, V1, V2? Elastic Collision: M1 = M2. The initial velocity of M1 is +V; M2 is zero. The final velocities of M1 and M2, respectively, are: 1. 2. 3. 4. Zero, V/2 -V, V Zero, V V/2, V/2 Inelastic Collision: Make a prediction Inelastic Collision: M1 = M2. The initial velocity is V. The final velocity is: 1. 2. 3. 4. 2V Zero V V/2 A matter of the point of view…. • Imagine how a collision looks, when viewed from a video camera that is moving. “Real world.” 2v M M V Here’s what the film sees…. “Film world.” v v M M Before collision, the film shows two blocks of same mass approaching at the same speed. “Real world.” M 2v M V In the film, two identical masses approach velocity +V and –V respectively. After the collision, the velocity is 1. 2. 3. 4. Zero, Zero -V, +V -V/2, +V/2 +V, -V (no change) Here’s what the film sees…. “Film world.” v v M M Before collision, the film shows two blocks of same mass approaching at the same speed. After the collision, the blocks move apart with equal speed. v v M M If that’s what the film “saw”, what happened in the “real world”?…. “Film world.” After the collision, the blocks move apart with equal speed. v v M M V VRe al VFilm VCamera “Real world.” 2v V=0 M M Actually, both situations describe “real” physics. Momentum is conserved in both cases.