Download Chapter 11a

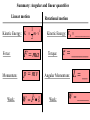
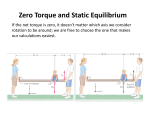
Announcements
1. Midterm 2 on Wednesday, Oct. 19.
2. Material: Chapters 7-11
3. Review on Tuesday (outside of class time)
4. I’ll post practice tests on Web
5. You are allowed a 3x5 inch cheat card
6. Go through practice exams & homework & class
examples; understand concepts & demos
7. Time limit for test: 50 minutes
Conservation of energy (including rotational energy):
Again:
If there are no non-conservative forces: Energy is conserved.
Rotational kinetic energy must be included in energy
considerations!
Ei  E f
U i  Klinear,initial  K rotational,initial  U f  Klinear, final  K rotational, final
Black board example 11.5
Connected cylinders.
Two masses m1 (5 kg) and m2 (10
kg) are hanging from a pulley of
mass M (3 kg) and radius R (0.1
m), as shown. There is no slip
between the rope and the pulleys.
(a) What will happen when the
masses are released?
(b) Find the velocity of the masses after they have fallen a
distance of 0.5 m.
(c) What is the angular velocity of the pulley at that moment?
Torque
F  sin f
r
F
f
F  cos f
A force F is acting at an angle f on a lever that is rotating around
a pivot point. r is the ______________ between F and the pivot
point.
This __________________ pair results in a torque t on the lever
t  r  F  sin f
Black board example 11.6
Two mechanics are trying to
open a rusty screw on a ship
with a big ol’ wrench. One
pulls at the end of the wrench
(r = 1 m) with a force F = 500
N at an angle F1 = 80 °; the
other pulls at the middle of
wrench with the same force
and at an angle F2 = 90 °.
What is the net torque the two mechanics are applying to the screw?
Torque t and
angular acceleration a.
Newton’s __________ law for rotation.
Particle of mass m rotating in a
circle with radius r.
force Fr to keep particle
on circular path.
force Ft accelerates
particle along tangent.
Ft  mat
Torque acting on particle is ________________
to angular acceleration a:
t  Ia
 
dW  F  ds
 
W  F s
Definition of work:
Work in linear motion:
 
dW  F  ds
 
W  F  s  F  s  cos 
Component of force F along
displacement s. Angle 
between F and s.
Work in rotational motion:
 
dW  F  ds
Torque t and angular
dW  t  ___
W  t  ___
displacement q.
Work and Energy in rotational motion
Remember work-kinetic energy theorem for linear motion:
1
1
2
2
W

mv

mv

f
i
2
2
External work done on an object changes its __________ energy
There is an equivalent work-rotational kinetic energy theorem:
1
1
2
2
W  2 ___  f  2 ___ i
External, rotational work done on an object changes its _______________energy
Linear motion with constant
linear acceleration, a.
Rotational motion with constant
rotational acceleration, a.
v xf  v xi  a x t
 f  _________
x f  xi  12 (vxi  vxf )t
q f  ________________
1 2
x f  xi  v xi t  a x t
2
q f  ____________________
vxf  vxi  2ax ( x f  xi )
 f  ___________________
2
2
2
Summary: Angular and linear quantities
Linear motion
1
2
K

m

v
Kinetic Energy:
2
Force:
F  ma
Momentum:
p  mv
Work:
 
W  F s
Rotational motion
Kinetic Energy: K R  _________
Torque:
t  ______
Angular Momentum:
Work:
L  __
W  _____
Rolling motion
Pure rolling:
There is no ___________
Linear speed of center of mass:
vCM
ds R  dq


 R 
dt
dt
Rolling motion
The _______ __________
of any point on the wheel
is the same.
The linear speed of any point on the object changes as shown in the
diagram!!
For one instant (bottom), point P has _______ linear speed.
For one instant (top), point P’ has a linear speed of ____________
Rolling motion of a particle on a wheel
(Superposition of ________ and ___________ motion)
Rolling
=
Rotation
+
Linear
Rolling motion
Superposition principle:
Rolling motion
=
Kinetic energy
of rolling motion:
Pure _________ +
Pure _______
1
1
K  ____  I CM ____
2
2
Chapter 11: Angular Momentum part 1
Reading assignment: Chapter 11.4-11.6
Homework : (due Monday, Oct. 17, 2005):
Problems:
30, 41, 42, 44, 48, 53
• Torque
• Angular momentum
• Angular momentum is conserved
Torque and the ______________
Thus far:
Torque
t  r  F  sin F
Torque is the _____________
between the force vector F
and vector r
 
t  r F

Torque and the vector product
Definition of vector product:
f
  
C  A B
- The vector product of vectors A and B is the ___________.
- C is _________________ to A and B
- The __________________ of is C = A·B·sinf
Torque and the vector product
  
C  A B
f
Use the right hand rule to figure out the direction of C.
- __________ is C (or torque t, angular velocity , angular momentum L)
- _____________ finger is A (or radius r)
- ____________ finger is B (or force F)
Torque and the vector product
  
C  A B
f
Rules for the vector product.
 
 
1. A  B   B  A
 
 
Thus, A  A  0
2. If A is ______ to B then A  B  0.
 
A B  A B
3. If A is _______ to B then
  
   
4. A  ( B  C )  A  B  A  C
5. Magnitude of C = A·B·sinq is equal to area of ______________
made by A and B
Torque and the vector product
  
C  A B
f
Rules for the vector product (cont).

 


6. A  B  ( Ay Bz  Az B y )i  ( Ax Bz  Az Bx ) j  ( Ax B y  Ay Bx )k
Black board example 12.2
HW 21
A force F = (2.00i + 3.00j) is
applied to an object that is
pivoted about a fixed axis
aligned along the z-axis.
The force is applied at the point
r = (4.00i + 5.00j).
(a) What is the torque exerted on the object?
(b) What is the magnitude and direction of the torque vector t.
(c) What is the angle between the directions of F and r?