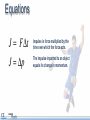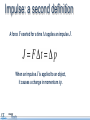* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download The Physics of Renewable Energy
Monte Carlo methods for electron transport wikipedia , lookup
Hamiltonian mechanics wikipedia , lookup
Renormalization group wikipedia , lookup
Velocity-addition formula wikipedia , lookup
Atomic theory wikipedia , lookup
Routhian mechanics wikipedia , lookup
Centripetal force wikipedia , lookup
Symmetry in quantum mechanics wikipedia , lookup
Tensor operator wikipedia , lookup
Old quantum theory wikipedia , lookup
Relativistic quantum mechanics wikipedia , lookup
Special relativity wikipedia , lookup
Uncertainty principle wikipedia , lookup
Rigid body dynamics wikipedia , lookup
Classical mechanics wikipedia , lookup
Center of mass wikipedia , lookup
Mass in special relativity wikipedia , lookup
Laplace–Runge–Lenz vector wikipedia , lookup
Mass versus weight wikipedia , lookup
Quantum vacuum thruster wikipedia , lookup
Work (physics) wikipedia , lookup
Electromagnetic mass wikipedia , lookup
Matter wave wikipedia , lookup
Equations of motion wikipedia , lookup
Accretion disk wikipedia , lookup
Classical central-force problem wikipedia , lookup
Theoretical and experimental justification for the Schrödinger equation wikipedia , lookup
Angular momentum wikipedia , lookup
Photon polarization wikipedia , lookup
Angular momentum operator wikipedia , lookup
Specific impulse wikipedia , lookup
Relativistic mechanics wikipedia , lookup
Newton's laws of motion wikipedia , lookup
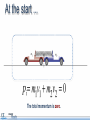
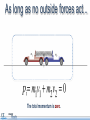
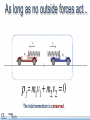
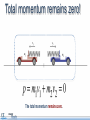
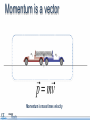
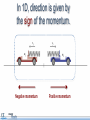
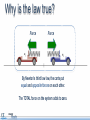
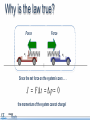
Momentum and Impulse Objectives • Calculate the momentum of an object. • Identify the units of momentum. • Calculate the momentum of a physical system consisting of multiple objects moving in different directions. • Calculate the change in momentum of an object. • Define impulse and its units. • Calculate the impulse applied to a physical system Objectives • Define the law of conservation of momentum. • Demonstrate the law of conservation of momentum using an interactive simulation. • Apply the law of conservation of momentum in one dimension. Physics terms • momentum • Impulse • law of conservation of momentum Equations The momentum of an object is its mass multiplied by its velocity. Momentum is a vector. Equations Impulse is force multiplied by the time over which the force acts. The impulse imparted to an object equals its change in momentum. Equations Conservation of momentum: Momentum before = Momentum after What does momentum mean? How is the word momentum used in everyday life? Can you think of an example? How is the physics definition of the word different from the everyday usage? Consider these two objects A one kilogram sphere is moving at 100 meters per second. A 100 kilogram sphere is moving at one meter per second. Consider these two objects If the same stopping force is applied to each, which sphere will stop first? Consider these two objects If the same stopping force is applied to each, which sphere will stop first? A. The 100 kg sphere B. The 1 kg sphere C. It’s a tie. D. More information is needed. Consider these two objects If the same stopping force is applied to each, which sphere will stop first? A. The 100 kg sphere B. The 1 kg sphere C. It’s a tie! D. More information is needed. Consider these two objects If the same stopping force is applied to each, which sphere will stop first? A. The 100 kg sphere B. The 1 kg sphere C. It’s a tie! D. More information is needed. Why? Momentum Momentum is the product of mass and velocity. p = mv Momentum was originally identified with a moving object’s persistence of motion. Momentum Momentum is the product of mass and velocity. p = mv The spheres have the same momentum. p = 100 kg m/s p = 100 kg m/s Test your knowledge A red truck and a blue truck have the same mass. The red truck is parked, and the blue truck is traveling along the highway at 60 mph. a) Do both trucks have inertia? b) Do both trucks have momentum? Test your knowledge A red truck and a blue truck have the same mass. The red truck is parked, and the blue truck is traveling along the highway at 60 mph. a) Do both trucks have inertia? Yes. All objects with mass have inertia. They resist having their motion changed. b) Do both trucks have momentum? Test your knowledge A red truck and a blue truck have the same mass. The red truck is parked, and the blue truck is traveling along the highway at 60 mph. a) Do both trucks have inertia? Yes. All objects with mass have inertia. They resist having their motion changed. b) Do both trucks have momentum? No. The blue truck has momentum. The red truck has NO momentum because it has zero velocity. Momentum is sometimes referred to as “inertia in motion”. Units of momentum Momentum has units of mass multiplied by velocity. mass in kg velocity in m/s Engaging with the concepts What is the momentum of a 60 kg sprinter running at 7.0 m/s? Momentum 60 7.0 Engaging with the concepts What is the momentum of a 60 kg sprinter running at 7.0 m/s? 420 kg m/s What is the velocity of the sprinter if her momentum is 270 kg m/s? Momentum 420 60 7.0 Engaging with the concepts What is the momentum of a 60 kg sprinter running at 7.0 m/s? 420 kg m/s What is the velocity of the sprinter if her momentum is 270 kg m/s? 4.5 m/s If she wanted to double her momentum, how fast would she have to run? Velocity 270 60 4.5 Engaging with the concepts What is the momentum of a 60 kg sprinter running at 7.0 m/s? 420 kg m/s What is the velocity of the sprinter if her momentum is 270 kg m/s? 4.5 m/s If she wanted to double her momentum, how fast would she have to run? twice as fast (9.0 m/s) Velocity 540 60 9.0 Engaging with the concepts A 2,000 kg car and a 4,000 kg truck are both traveling at 10 m/s when they hit a wall. Which has more momentum before impact? Momentum 4000 What is the ratio of their momenta? 10 Engaging with the concepts A 2,000 kg car and a 4,000 kg truck are both traveling at 10 m/s when they hit a wall. Which has more momentum before impact? the truck Momentum 40000 What is the ratio of their momenta? ptruck: pcar is 2:1 4000 10 Engaging with the concepts A boulder is dropped from rest and hits the ground at a speed of 15 m/s, transferring 1,200 kg m/s of momentum to the Earth. What is its mass? Mass 1200 15 Engaging with the concepts A boulder is dropped from rest and hits the ground at a speed of 15 m/s, transferring 1,200 kg m/s of momentum to the Earth. What is its mass? 80 kg Mass 1200 80 15 Engaging with the concepts Create two objects with a momentum of 100 kg m/s, but with masses of 1.0 kg and 4.0 kg. Velocity 100 If the mass is four times greater, how does the velocity change? 1.0 Engaging with the concepts Create two objects with a momentum of 100 kg m/s, but with masses of 1.0 kg and 4.0 kg. Velocity 100 If the mass is four times greater, how does the velocity change? The velocity is one-fourth as much. 1.0 100 Momentum Momentum is a vector. Momentum Momentum is a vector. For one-dimensional motion, this means the direction of motion determines the sign of an object’s momentum. p = -100 kg m/s p = +100 kg m/s Momentum of a system What is the total momentum of this system of two balls? A. Zero B. +100 kg m/s A. +200 kg m/s p = -100 kg m/s p = +100 kg m/s Momentum of a system What is the total momentum of this system of two balls? A. Zero! 100 kg m/s + -100kg m/s = 0 kg m/s A. +100 kg m/s A. +200 kg m/s p = -100 kg m/s p = +100 kg m/s Assessment 1. Calculate the momentum of a 1.0 kg object moving with a velocity of +20 m/s. 2. What is the velocity of an object that has a momentum of -30 kg m/s and a mass of 3.0 kilograms? 3. Two objects have equal momentum but one has four times the mass of the other. What is the relationship between their velocities? Assessment 1. Calculate the momentum of a 1.0 kg object moving with a velocity of +20 m/s. p = mv = (1.0 kg)(20 m/s) = +20 kg m/s 2. What is the velocity of an object that has a momentum of -30 kg m/s and a mass of 3.0 kilograms? 3. Two objects have equal momentum but one has four times the mass of the other. What is the relationship between their velocities? Assessment 1. Calculate the momentum of a 1.0 kg object moving with a velocity of +20 m/s. p = mv = (1.0 kg)(20 m/s) = +20 kg m/s 2. What is the velocity of an object that has a momentum of -30 kg m/s and a mass of 3.0 kilograms? If p = mv, then v = p/m = (-30 kg m/s)/(3.0 kg) = -10 m/s 3. Two objects have equal momentum but one has four times the mass of the other. What is the relationship between their velocities? Assessment 1. Calculate the momentum of a 1.0 kg object moving with a velocity of +20 m/s. p = mv = (1.0 kg)(20 m/s) = +20 kg m/s 2. What is the velocity of an object that has a momentum of -30 kg m/s and a mass of 3.0 kilograms? If p = mv, then v = p/m = (-30 kg m/s)/(3.0 kg) = -10 m/s 3. Two objects have equal momentum but one has four times the mass of the other. What is the relationship between their velocities? The lighter object is moving 4 times faster. Assessment 4. Which answer below shows the correct units for momentum? A. kg m/s2 B. kg m2/s2 C. kg m/s D. kg s/m Assessment 4. Which answer below shows the correct units for momentum? A. kg m/s2 B. kg m2/s2 C. kg m/s D. kg s/m Assessment 5. Two bowling balls each have a mass of 4.0 kg. The red ball is moving east at 2.0 m/s. The blue ball is moving west at 1.0 m/s. Calculate the total momentum of the system. Assessment 5. Two bowling balls each have a mass of 4.0 kg. The red ball is moving east at 2.0 m/s. The blue ball is moving west at 1.0 m/s. Calculate the total momentum of the system. Impulse Changes in momentum The momentum of an object changes as it speeds up or slows down. Changes in momentum The momentum of an object changes as it speeds up or slows down. For example, this 2000 kg car slows to a stop and loses its momentum. Impulse A change in momentum is called an impulse, J. Since impulse is the change in momentum, it has the same units as momentum: kg m/s. Impulse A 1000 kg car is initially parked. It accelerates to 15 m/s. a) What is its change in momentum? Impulse A 1000 kg car is initially parked. It accelerates to 15 m/s. a) What is its change in momentum? b) What is the impulse? Impulse A 1000 kg car is initially parked. It accelerates to 15 m/s. a) What is its change in momentum? b) What is the impulse? the same! Calculating impulse A 500 gram ball of clay is falling at -2.0 m/s when it strikes the ground. It sticks to the ground without bouncing. What is the impulse on the clay during the collision? (Watch out for signs!) -2.0 m/s Calculating impulse A 500 gram ball of clay is falling at -2.0 m/s when it strikes the ground. It sticks to the ground without bouncing. What is the impulse on the clay during the collision? (Watch out for signs!) -2.0 m/s Calculating impulse +2.0 m/s A 500 gram superball is falling at 2.0 m/s when it strikes the ground. It bounces back up at 2.0 m/s. Will the impulse on the superball be greater than or less than the impulse on the clay? -2.0 m/s Calculating impulse +2.0 m/s A 500 gram superball is falling at 2.0 m/s when it strikes the ground. It bounces back up at 2.0 m/s. Will the impulse on the superball be greater than or less than the impulse on the clay? -2.0 m/s The impulse on the superball will be greater! It doesn’t just come to a stop. It reverses direction! Calculate the impulse. Calculating impulse +2.0 m/s A 500 gram superball is falling at 2.0 m/s when it strikes the ground. It bounces back up at 2.0 m/s. Calculate the impulse: -2.0 m/s Twice as much impulse as the clay ball! Impulse There are many ways to deliver the same impulse. Here are three ways to apply an impulse to slow down a car. In each case the impulse J = Δp is the same. What is different? Impulse The time the impulse is applied is different in each case. If the time decreases, then the force must increase to supply the same impulse. Impulse: a second definition A force F exerted for a time Δt applies an impulse J. When an impulse J is applied to an object, This definition of impulse leads to it causes a change in momentum Δp. a second set of units for impulse: Units This second definition for impulse gives us a second set of units for impulse: newton-seconds, or N s. Impulse units: N s = kg m/s Engaging with the concepts What impulse is imparted to a car if a force of 500 N is applied for 3.0 seconds? 500 Impulse 3.0 Engaging with the concepts What impulse is imparted to a car if a force of 500 N is applied for 3.0 seconds? 500 Impulse 1500 3.0 Engaging with the concepts If the force on the car is doubled, what happens to the impulse? 1000 If the time that the force is exerted triples, what happens to the impulse? Impulse 3.0 Engaging with the concepts If the force on the car is doubled, what happens to the impulse? it doubles 1000 Impulse 3000 If the time that the force is exerted triples, what happens to the impulse? 3.0 it triples Impulse is directly proportional to force and to time. Impulse is a vector Impulse J is a vector. Impulse can be positive or negative for motion along a line. The direction of the force determines the direction of the impulse. Engaging with the concepts Jonathan applies his brakes for 0.50 s, which imparts an impulse of 1000 N s. Force What force did the brakes apply to slow down the car? -1000 0.50 1000 Engaging with the concepts Jonathan applies his brakes for 0.50 s, which imparts an impulse of -1000 N s. -2000 What force did the brakes apply to slow down the car? -2000 N Force -1000 0.50 1000 A negative force gives a negative impulse. Click [Run] to observe the effect on the car. Applying what you’ve learned To change an object’s momentum, you can apply •a large force for a short time OR •a small force for a long time. Describe some situations where you want to apply a smaller force for a longer time. Applying what you’ve learned How do we decrease the force by increasing the time in these cases? • Car collisions • Sports collisions Applying what you’ve learned How do we decrease the force by increasing the time in these cases? • Car collisions bumpers to protect the car, air bags and seat belts to protect people • Sports collisions helmets and padding to reduce concussions and broken bones Assessment 1. Calculate the change in momentum of a 1000 kg car that speeds up from 10 m/s to 15 m/s. Assessment 1. Calculate the change in momentum of a 1000 kg car that speeds up from 10 m/s to 15 m/s. Assessment 2. Which set of units below is NOT correct for impulse? A. kg m/s B. N s C. kg m2/s Assessment 2. Which set of units below is NOT correct for impulse? A. kg m/s B. N s C. kg m2/s Answer C is NOT correct. Answers A and B are BOTH correct. Assessment 3. A 2.0 kg rocket is subjected to a constant force of 400 N that accelerates it from rest to a speed of 100 m/s. a) What is the impulse applied to the rocket? b) How long did this event last? Assessment 3. A 2.0 kg rocket is subjected to a constant force of 400 N that accelerates it from rest to a speed of 100 m/s. a) What is the impulse applied to the rocket? b) How long did this event last? Assessment 3. A 2.0 kg rocket is subjected to a constant force of 400 N that accelerates it from rest to a speed of 100 m/s. a) What is the impulse applied to the rocket? b) How long did this event last? J = F∆ t Advanced Newton’s second law can now be written in a different way: Substitute in for the acceleration: Advanced This form of Newton’s second law can even apply to situations where the mass of an object changes. Conservation of momentum Conservation laws In a closed system, energy is conserved. Conservation laws Consider this closed system containing ... two frictionless carts with opposing springs. Conservation laws The carts start pinned together Consider this closed system containing ... two frictionless carts with opposing springs. Conservation laws When the pin is released, the carts will fly away from each other. How fast will does each one go? Energy conservation Energy conservation The elastic energy in the two springs . . . Energy conservation The elastic energy in the two springs equals the kinetic energy of both carts after the release. Energy conservation v1 This is one equation (conservation of energy) with two unknowns: v1 and v2. We can’t solve for the final velocities! v2 Not enough information v1 v2 Energy conservation does not tell us whether the carts move at the same speed or at different speeds. Not enough information v1 v2 Energy conservation does not tell us that the carts move in opposite directions, although we know that they do. A second law is needed! Suppose the carts have different masses. A second law is needed! Suppose the carts have different masses. Are the final speeds still the same? A second law is needed! Energy conservation says nothing about how the two velocities compare with each other. What patterns do you see? Mass, velocity, momentum, and energy data Equal masses equal speeds Mass, velocity, momentum, and energy data Twice the mass half the speed Mass, velocity, momentum, and energy data Triple the mass 1/3 the speed Mass, velocity, momentum, and energy data Triple the mass 1/3 the speed Mass, velocity, momentum, and energy data What principle is operating here? Notice that the momentum is equal and opposite! Examining the momentum Mass, velocity, momentum, and energy data Conservation of momentum Conservation of momentum The total momentum of a closed system remains constant. Momentum Momentum is mass times velocity At the start ... The total momentum is zero. As long as no outside forces act... The total momentum is zero. As long as no outside forces act... The total momentum is conserved. One cart’s momentum is positive .. . Mass, velocity, momentum, and energy data The other cart’s momentum is negative Mass, velocity, momentum, and energy data Total momentum remains zero! The total momentum remains zero. Momentum is a vector Momentum is mass times velocity In 1D, direction is given by the sign of the momentum. Negative momentum Positive momentum Why is the law true? Force Force By Newton’s third law law, the carts put equal and opposite forces on each other. The TOTAL force on the system adds to zero. Why is the law true? Force Force Since the net force on the system is zero . . . the momentum of the system cannot change! Apply momentum conservation A 6.0 kg package explodes into two pieces, A and B. Piece A, with a mass of 4.0 kg, moves east at 10 m/s. a) What is the mass of piece B? B b) What is the direction of piece B? c) What is the speed of piece B? A 4.0 kg 10 m/s Apply momentum conservation A 6.0 kg package explodes into two pieces, A and B. Piece A, with a mass of 4.0 kg, moves east at 10 m/s. a) What is the mass of piece B? 2.0 kg B b) What is the direction of piece B? c) What is the speed of piece B? A 4.0 kg 10 m/s Apply momentum conservation A 6.0 kg package explodes into two pieces, A and B. Piece A, with a mass of 4.0 kg, moves east at 10 m/s. a) What is the mass of piece B? 2.0 kg B b) What is the direction of piece B? west c) What is the speed of piece B? A 4.0 kg 10 m/s Apply momentum conservation A 6.0 kg package explodes into two pieces, A and B. Piece A, with a mass of 4.0 kg, moves east at 10 m/s. a) What is the mass of piece B? 2.0 kg B b) What is the direction of piece B? west c) What is the speed of piece B? A 4.0 kg Apply conservation of momentum 10 m/s Apply momentum conservation A 6.0 kg package explodes into two pieces, A and B. Piece A, with a mass of 4.0 kg, moves east at 10 m/s. c) What is the speed of piece B? Assessment 1. Which statement below correctly summarizes the law of conservation of momentum? A. The momentum of an object always remains constant. B. The momentum of a closed system always remains constant. C. Momentum can be stored in objects such as a spring. D. All of the above. Assessment 1. Which statement below correctly summarizes the law of conservation of momentum? A. The momentum of an object always remains constant. B. The momentum of a closed system always remains constant. C. Momentum can be stored in objects such as a spring. D. All of the above. Assessment 2. An astronaut with a mass of 100 kg throws a wrench with a mass of 2.0 kg at a velocity of 5.0 m/s. What is the recoil velocity of the astronaut if both wrench and astronaut are initially at rest? Assessment This example is physically similar to the ballistic carts! Assessment 2. An astronaut with a mass of 100 kg throws a wrench with a mass of 2.0 kg at a velocity of 5.0 m/s. What is the recoil velocity of the astronaut if both wrench and astronaut are initially at rest? Momentum before throwing wrench = Momentum after throwing wrench The unknown velocity! Assessment 2. An astronaut with a mass of 100 kg throws a wrench with a mass of 2.0 kg at a velocity of 5.0 m/s. What is the recoil velocity of the astronaut if both wrench and astronaut are initially at rest? Momentum before throwing wrench = Initial momentum is zero! Momentum after throwing wrench Assessment 2. An astronaut with a mass of 100 kg throws a wrench with a mass of 2.0 kg at a velocity of 5.0 m/s. What is the recoil velocity of the astronaut if both wrench and astronaut are initially at rest? Momentum before throwing wrench = Momentum after throwing wrench