Download Complex Geometries and Higher Reynolds Numbers

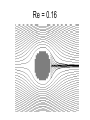
Complex Geometries and
Higher Reynolds Numbers
Creating obstacle files
• Current LB2D_Prime
naming convention:
– sizexXsizey.bmp
• Current format:
– ‘True color’ 24 bit
Scaling to real world
• Choose a Reynolds number
• Choose a combination of slit width and viscosity to give
maximum velocity < ≈0.1 lu ts-1; smaller is better
• Maximum velocity 3/2 of average for Poiseuille flow in slit
• Best to use t = 1 for simple bounceback boundaries:
yields kinematic viscosity of 1/6 lu2 ts-1
• Solve for the gravitational acceleration needed to drive
the flow by rearranging Poiseuille equation
Entry Length Effects
•
•
•
r is the 'radius' -- the distance from
the center to the point of interest
a is the half-width (d/2)
u is the velocity at the point of
interest and uavg is the average
velocity
Tritton DJ (1988) Physical Fluid Dynamics, 2nd Ed. Oxford
University Press, Oxford New York
x /(d Re) is dimensionless distance down the pipe. When this distance is infinite, Poiseuille flow
is fully developed. If Re = 1, Poiseuille flow is well-developed in a short distance down the pipe:
x/d = 1 → x = d = 2a (just 2 half-widths down the pipe). As the Reynolds number increases, this
distance can become quite large. If x = 1 m with Re = 103 in a 10 cm pipe, x/(d Re) = 1 m /(10-1
m 103) = 10-2 and Poiseuille flow will not be fully developed even 1 m from the inlet.
Entry Length Effects
Tritton DJ (1988) Physical Fluid Dynamics, 2nd Ed. Oxford
University Press, Oxford New York
Velocity BCs
• Simple compressible fluid model
• Identical constant velocities at each end of the domain:
– mass of fluid will change with time
• Flow must be accompanied by a pressure gradient and hence the
pressure must be lower at the outlet
• The pressure and density are related through an ideal gas law of the
form P = r/3 in this model
• Densities at the input and output must be different
• If the velocity boundaries on each end of the domain are equal,
mass will accumulate in the system because the mass flux of fluid in
(vin rin) will exceed the out flux (vout rout)
• Problem increases in severity as the pressure difference increases
• Incompressible model of Zou and He (1997), pressure boundaries,
or gravity-driven flow can be used to avoid this complication
Flow Past a Cylinder
• The drag force FD is defined in terms of
the drag coefficient CD as
FD  rr u CD
2
0
• Gravitational Force
F  rg LW  r
2

http://scienceworld.wolfram.com/physics/CylinderDrag.html
Tritton DJ (1988) Physical Fluid Dynamics, 2nd Ed. Oxford
University Press, Oxford New York
Re = 0.16
Re = 41
Taneda S (1956)
von Kármán Vortex Street, Re = 105
h / l  (1 /  ) sinh 1 (l )  0.281
h
l
Photo by S. Taneda. S. Taneda and the Society for Science on Form, Japan
von Kármán Vortex Street, Re = 105:
LBM Simulation (vorticity)