* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Chapter 9
Flow conditioning wikipedia , lookup
Water supply network wikipedia , lookup
Navier–Stokes equations wikipedia , lookup
Water metering wikipedia , lookup
Fluid dynamics wikipedia , lookup
Computational fluid dynamics wikipedia , lookup
Reynolds number wikipedia , lookup
Derivation of the Navier–Stokes equations wikipedia , lookup
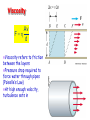
Chapter 9 Solids and Fluids (c) EXAMPLE A small swimming pool has an area of 10 square meters. A wooden 4000-kg statue of density 500 kg/m3 is then floated on top of the pool. How far does the water rise? Note: Density of water = 1000 kg/m3 Solution Given: rwood/rH20 = 0.5, A = 10 m2, M = 4000 kg Find: h h Level is the same as if 4000 kg of water were added = 4 m3 Consider problem: A volume V = 4 m3 of water is added to a swimming pool. What is h? h V / A = 40 cm Quiz 1. What is your section number? 2. Three objects rest on bathroom scales at a lake bottom. Object 1 is a lead brick of volume 0.2 m3 Object 2 is a gold brick of volume 0.2 m3 Object 3 is a lead brick of volume 0.1 m3 DATA: specific gravity of lead = 11.3 specific gravity of gold = 19.3 specific gravity of mercury = 13.6 Which statement is true? a) #1 and #2 have the same buoyant force b) #1 and #2 register the same weights on the scales c) #1 and #3 have the same buoyant force d) #1 and #3 register the same weights on the scales e) If the lake were filled with mercury, the scales would not change. Equation of Continuity What goes in must come out! mass density M rAx rAvt Mass that passes a point in pipe during time t Eq. of Continuity r1 A1v1 r 2 A2v2 Example Water flows through a 4.0 cm diameter pipe at 5 cm/s. The pipe then narrows downstream and has a diameter of of 2.0 cm. What is the velocity of the water through the smaller pipe? Solution Eq. of Continuity r1 A1v1 r 2 A2v2 A1v1 A2 v2 r12 v2 2 v1 4v1 = 20 cm/s r2 Laminar Flow and Turbulence Laminar or Streamline Flow: Fluid elements move along smooth paths that don’t cross Friction in laminar flow is called viscosity Turbulent flow Irregular paths Sets in for high gradients (large velocities or small pipes) Ideal Fluids Laminar Flow No turbulence Non-viscous No friction between fluid layers Incompressible Density is same everywhere Bernoulli’s Equation 1 2 P rv rgy constant 2 Physical content: the sum of the pressure, kinetic energy per unit volume, and the potential energy per unit volume has the same value at all points along a streamline. How can we derive this? Bernoulli’s Equation: derivation Physical basis: Work-energy relation All together now: With We get: Example: Venturi Meter A very large pipe carries water with a very slow velocity and empties into a small pipe with a high velocity. If P2 is 7000 Pa lower than P1, what is the velocity of the water in the small pipe? Solution Given: P = 7000 Pa, r = 1000 kg/m3 Find: v Basic formula 1 2 P rgh rv constant 2 1 2 P1 P2 rv 2 2P 2 v v = 3.74 m/s r Applications of Bernoulli’s Equation •Venturi meter •Curve balls •Airplanes Beach Ball Demo Example a Water drains out of the bottom of a cooler at 3 m/s, what is the depth of the water above the valve? b Solution Basic formula 1 2 P rgh rv constant 2 Compare water at top(a) of cooler with water leaving valve(b). 1 2 1 2 Pa rgha rva Pb rghb rvb 2 2 v2 h = 45.9 cm 2g Three Vocabulary Words •Viscosity •Diffusion •Osmosis Viscosity Av F d Viscosity refers to friction between the layers Pressure drop required to force water through pipes (Poiselle’s Law) At high enough velocity, turbulence sets in Diffusion Molecules move from region of high concentration to region of low concentration Fick’s Law: Mass C2 C1 Diffusion rate DA time L D = diffusion coefficient Osmosis Osmosis is the movement of water through a boundary while denying passage to specific molecules, e.g. salts