Download Chapter 9

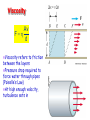
Chapter 9
Solids and Fluids (c)
EXAMPLE
A small swimming pool has an area of 10
square meters. A wooden 4000-kg statue of
density 500 kg/m3 is then floated on top of
the pool. How far does the water rise?
Note: Density of water = 1000 kg/m3
Solution
Given: rwood/rH20 = 0.5, A = 10 m2, M = 4000 kg
Find: h
h
Level is the same as if
4000 kg of water
were added = 4 m3
Consider problem: A volume V = 4 m3 of water is added
to a swimming pool. What is h?
h V / A
= 40 cm
Quiz
1. What is your section number?
2. Three objects rest on bathroom scales at a lake bottom.
Object 1 is a lead brick of volume 0.2 m3
Object 2 is a gold brick of volume 0.2 m3
Object 3 is a lead brick of volume 0.1 m3
DATA: specific gravity of lead = 11.3
specific gravity of gold = 19.3
specific gravity of mercury = 13.6
Which statement is true?
a) #1 and #2 have the same buoyant force
b) #1 and #2 register the same weights on the scales
c) #1 and #3 have the same buoyant force
d) #1 and #3 register the same weights on the scales
e) If the lake were filled with mercury, the scales would not
change.
Equation of Continuity
What goes in must come out!
mass density
M  rAx  rAvt
Mass that passes a point
in pipe during time t
Eq. of Continuity
r1 A1v1  r 2 A2v2
Example
Water flows through a 4.0 cm diameter pipe at 5
cm/s. The pipe then narrows downstream and has a
diameter of of 2.0 cm. What is the velocity of the
water through the smaller pipe?
Solution
Eq. of Continuity
r1 A1v1  r 2 A2v2
A1v1  A2 v2
r12
v2  2 v1  4v1 = 20 cm/s
r2
Laminar Flow and Turbulence
Laminar
or Streamline Flow:
 Fluid elements move along smooth paths that don’t cross
 Friction in laminar flow is called viscosity
Turbulent flow
 Irregular paths
 Sets in for high gradients (large velocities or small pipes)
Ideal Fluids
Laminar
Flow
 No turbulence
Non-viscous
 No friction between fluid layers
Incompressible
 Density is same everywhere
Bernoulli’s Equation
1 2
P  rv  rgy  constant
2
Physical content:
the sum of the pressure, kinetic energy per unit
volume, and the potential energy per unit volume
has the same value at all points along a streamline.
How can we derive this?
Bernoulli’s Equation: derivation
Physical basis: Work-energy relation
All together now:
With
We get:
Example: Venturi Meter
A very large pipe carries
water with a very slow
velocity and empties into
a small pipe with a high
velocity. If P2 is 7000 Pa
lower than P1, what is the
velocity of the water in
the small pipe?
Solution
Given: P = 7000 Pa, r = 1000 kg/m3
Find: v
Basic formula
1 2
P  rgh  rv  constant
2
1 2
P1  P2  rv
2
2P
2
v 
v = 3.74 m/s
r
Applications of Bernoulli’s Equation
•Venturi meter
•Curve balls
•Airplanes
Beach Ball Demo
Example
a
Water drains out of the bottom of a
cooler at 3 m/s, what is the depth of the
water above the valve?
b
Solution
Basic formula
1 2
P  rgh  rv  constant
2
Compare water at top(a) of
cooler with water leaving
valve(b).
1 2
1 2
Pa  rgha  rva  Pb  rghb  rvb
2
2
v2
h
= 45.9 cm
2g
Three Vocabulary Words
•Viscosity
•Diffusion
•Osmosis
Viscosity
Av
F
d
Viscosity
refers to friction
between the layers
Pressure drop required to
force water through pipes
(Poiselle’s Law)
At high enough velocity,
turbulence sets in
Diffusion
Molecules move from region of high concentration
to region of low concentration
Fick’s Law:
Mass
 C2  C1 
Diffusion rate 
 DA

time
 L 
D = diffusion coefficient
Osmosis
Osmosis is the movement of water through a
boundary while denying passage to specific
molecules, e.g. salts