Download Rotational Kinetic Energy

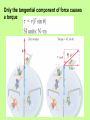
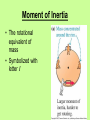
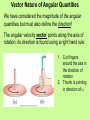
Chapter 8
Rotational Motion
Why rotational?
• We’ve focused on translational motion up
to this point
• Rotational motion has things in common
with translational motion
• Examples: spinning wheels,
washing machine drum,
merry-go-round, etc.
Angular Quantities
Quantities in linear motion have a
corresponding quantity in rotational motion
Angular Position
Angular displacement
is the angle (in rads)
through which a point
or line has been
rotated about an axis
Angular Velocity
The rate of change of
angular displacement ΔӨ
with time Δt
Instantaneous Angular Velocity
Angular Acceleration
The rate of change of angular velocity
Instantaneous
Acceleration
Period
• The time it takes to complete one cycle or
revolution. Also the reciprocal of the
frequency.
T=1
f
Look familiar?!
The equations of motion for constant angular
acceleration are the same as those for linear motion,
with the substitution of the angular quantities for the
linear ones.
Torque
From experience, we know that the same force will
be much more effective at rotating an object such
as a nut or a door if our hand is not too close to the
axis.
This is why we
have longhandled
wrenches, and
why
doorknobs are
not next to
hinges.
Torque
To make an object
start rotating, a
force is needed
A longer lever arm
is very helpful in
rotating objects.
• Torque
depends on
–The length of
the lever arm
r┴
–The force
applied F
Torque is calculated
Only the tangential component of force causes
a torque
Moment of Inertia
• The rotational
equivalent of
mass
• Symbolized with
letter I
Angular Momentum
Angular momentum-the product of
the angular velocity of a body and its
moment of inertia about the axis of
rotation. Depends on the mass of the
object and how it is distributed
Rotational Kinetic Energy
We have learned that the kinetic energy of an object
is
By substituting the rotational quantities, we find that
the rotational kinetic energy is:
An object that has both translational and rotational
motion must take both into account to find the total
KE
Rotational Kinetic Energy
Torque does work as it moves the wheel through an
angle θ:
A torque acting through an angular displacement
does work, just as a force acting through a
distance does.
The work-energy theorem still applies!
Vector Nature of Angular Quantities
We have considered the magnitude of the angular
quantities but must also define the direction!
The angular velocity vector points along the axis of
rotation; its direction is found using a right hand rule:
1. Curl fingers
around the axis in
the direction of
rotation
2. Thumb is pointing
in direction of ω
Vector Nature of Angular Quantities
Angular acceleration
and angular momentum
vectors also point along
the axis of rotation.
References
• Giancoli, Douglas. Physics: Principles
with Applications 6th Edition. 2009.
• Walker, James. AP Physics: 4th Edition.
2010
• Zitewitz. Physics: Principles and
Problems. 2004
• www.hyperphysics.com
• http://whs.wsd.wednet.edu/Faculty/Bus
se/MathHomePage/busseclasses/apph
ysics/studyguides/chapter7_2008/Chap
ter7StudyGuide2008.html
22