* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download 100 Lec11 06
Introduction to quantum mechanics wikipedia , lookup
Eigenstate thermalization hypothesis wikipedia , lookup
Classical mechanics wikipedia , lookup
Nuclear structure wikipedia , lookup
Centripetal force wikipedia , lookup
Tensor operator wikipedia , lookup
Laplace–Runge–Lenz vector wikipedia , lookup
Equations of motion wikipedia , lookup
Hunting oscillation wikipedia , lookup
Symmetry in quantum mechanics wikipedia , lookup
Angular momentum wikipedia , lookup
Heat transfer physics wikipedia , lookup
Classical central-force problem wikipedia , lookup
Angular momentum operator wikipedia , lookup
Photon polarization wikipedia , lookup
Theoretical and experimental justification for the Schrödinger equation wikipedia , lookup
Relativistic mechanics wikipedia , lookup
Newton's laws of motion wikipedia , lookup
Relativistic angular momentum wikipedia , lookup
Work (physics) wikipedia , lookup
Rotational spectroscopy wikipedia , lookup
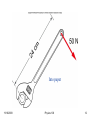
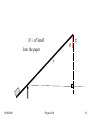
Physics 100 Fall 2005 Lecture 11 11/16/2009 Physics 100 1 Radians and Other Angular Units Define radian q R R q = 1 radian (rad.) 360o = 2p rad 180o = p rad 90o = p/2 rad etc. 1 rad 57.3o 11/16/2009 Physics 100 2 Vector or cross products C A B Note that this yields another vector (actually an axial vector) Contrast with the scalar product: q C A B 11/16/2009 A B yielding a scalar A B AB cos q Ax Bx Ay By Az Bz iˆ C Ax Bx ˆj Ay By C x Ay Bz Az B y kˆ Az Bz C y Az Bx Ax Bz C z Ax B y Ay Bx Physics 100 3 C A B C AB sin q To the plane of AB x C Right Hand Rule ‛x A Direction of advance of a right hand screw 11/16/2009 Physics 100 4 C A B Note that the vector product is not commutative A B B A Again look at Right Hand Rule x C A×B ‛x A B×A 11/16/2009 Physics 100 5 Relation between Angular and Linear Kinematics v s r s rq arc length v = rw a ra Different points on a rigid body do not Have the same s, v, a but do have the same q, w, a Direction of w is given by the right hand rule z Right hand Fingers are direction of q w Note: product is not y Thumb is direction of commutative v wr q r v x 11/16/2009 Physics 100 6 Point rotating a distance r from an axis v r P w out v wr Apply Right Hand Rule: Rotate w into r, right thumb points in direction of v 11/16/2009 Physics 100 7 Magnitude Direction v w r Vector vs. Axial Vector 11/16/2009 Physics 100 8 Rotational Dynamics y axis F4 O x F1 F2 F3 Forces pointing thru the axis (F1, F4) do not affect rotation Forces x, with lever arm ≠ 0, ( F2, F3), have maximal effect and the effect is proportional to the length of the lever arm. 11/16/2009 Physics 100 9 11/16/2009 Physics 100 10 Torque N r F (m·N) N in book N = r F sin q = r F when r F Torque is the rotational analog of force. 11/16/2009 Physics 100 11 Into paper 11/16/2009 Physics 100 12 N rF sin q q Into the paper F r 11/16/2009 Physics 100 13 Example: Compound Wheel, R1 =30 cm, R2=50 cm N R1F1 sin 90 R2 F2 sin 60 (0.30 N)(50 N) (0.5 m)(50 N)sin 60 6.7 mN Net torque acts to accelerate rotation clockwise. Right Hand Rule N points into the page 11/16/2009 Physics 100 14 Moment of Inertia a. k. a. rotational inertia Consider a collection of particles each having kinetic energy Ki = ½ mi vi2 = ½ mi ri2 w2 Rigid body Then the total kinetic energy of the rigid body is K=½ Define I = (S m r ) w (S m r ) 2 i i i i 2 2 Moment of inertia (kg m2) Rotational analog of mass 11/16/2009 Physics 100 15 11/16/2009 Physics 100 16 11/16/2009 Physics 100 17 Newton’s First Law for Rotation N r F F 0 N 0 massless rod An object at rest or in uniform rotational motion, in the absence of externally imposed torques, remains at rest or in uniform rotational motion. If you don’t do anything, nothing happens 11/16/2009 Physics 100 18 Statics and Equilibrium Statics: A special case of dynamics in which bodies remain at rest in static equilibrium. For a rigid body to be in equilibrium both linear and angular accelerations must be 0. F Fi 0 (net force = 0) Translational equilibrium: or the 3 scalar equations i Fx Fix 0 3 axes, all zero i Fy Fiy 0 i Fz Fiz 0 i 11/16/2009 Physics 100 19 Rotational equilibrium: N Ni 0 (net torque = 0) i again 3 scalar equations for the torques around 3 axes. Center of Gravity and Center of Mass: For g uniform, i . e. small heights above Earth’ surface the C. M. and the C. G. are coincident. i mi gxi i mi xi xCG xCM mi g mi i i similarly for y and z A translational force like gravity acts like the total force is F g mi acting downward at the C. G./C. M. i 11/16/2009 Physics 100 20 Experimental Determination of the C. G.: Suspend an object. Extending the line of suspension downward will pass thru the C. G. A B Hang from another point b a Dashed lines intersect at the C. G. C. G. 11/16/2009 Physics 100 21 Examples of Equilibrium: F1 F2 m F1 = -F2 translational F=0 F1 F2 r x 11/16/2009 N1 = -N2 = F1 r = -F2 r N=0 Physics 100 rotational 22 Stable, Unstable and Neutral Equilibrium Earth’s gravitational field g Potential energy as a function of position U unstable unstable neutral neutral stable stable 11/16/2009 Physics 100 23 For an extended body F or F F or F F or F C. M. is raised stable Pendulum with rigid cable C. M. falls unstable C. M. neither rises nor falls neutral unstable stable 11/16/2009 Physics 100 24 Tip Over Angle: mg mg Slides q q Tips over Arrows () refer to direction of mg from the CM not the magnitude. 11/16/2009 Physics 100 25 Newton’s Second Law for Rotation N r F F ma N mar (translational) everything is massless rod Recall from rotational kinematics a a r or in the case a a r N mr 2 a but, I mr 2 is just the moment of inertia N Ia or vectorially N Ia 11/16/2009 Physics 100 26 Angular momentum N=Ia Or N = DL / Dt Where L = I w is called the angular momentum Lrp L is another conserved quantity e. g. ice skater, piano stool, bicycle stability, gyroscopes, stellar collapse, etc. 11/16/2009 Physics 100 27 Conservation of angular momentum No net torque, decrease I => w must increase ad vice versa 11/16/2009 Physics 100 28 11/16/2009 Physics 100 29 Kepler’s Laws I. Planetary orbits are ellipses with the sun at one focus. f • f’ II. Equal fractional areas of the ellipses are swept out in equal times. Conservation of L 11/16/2009 Physics 100 30 Newton’s 3rd Law for rotation Conservation of angular momentum I f w f I iwi Action vs. reaction Twist something, something twists on you Action reaction pairs couples A pair of forces with equal magnitudes, opposite directions and different lines of action. 11/16/2009 Physics 100 31 What is the torque produced about the 3 axes A, B and C? A F N N A NB L 2 B F L 2 C At A, N 0 FL FL At C, N FL 0 FL L L N F F FL 2 2 At B, A couple produces a torque that does not depend on the location of the axis. 11/16/2009 Physics 100 32 Example: Stellar Collapse Inner core of a larger star collapses into a neutron star of very small radius r = rsun = 7 x 105 km, m = 2 msun,, T = 10 d, rn-star = 10 km Assume no mass is lost in collapse. What is n-star’ rate of rotation? Conservation of L: Ii I f w f I iwi w f I f wi 2 mr 2 2 I r 5 wi f n star i fi 2 fi 2 rn star If mrn2 star 5 1 r 2 1 7 105 km 1 f so f n star T rn star T 10 km (10d)(24 h /d)(3600 s /h) 6 103 Hz 11/16/2009 Physics 100 33 Rotational energy and work Work: Exert a torque through an angular displacement W Nq Potential energy is increased by the doing of work Kinetic energy of rotation 1 2 Kq I w 2 This makes conservation of the total energy a little more complicated 11/16/2009 Physics 100 34 Wheel rolling down incline m, I Wheel is at rest at top. Initial energy is all potential. U = mgh h v, w v wr At bottom wheel is rolling and has lost all its potential energy w.r.t. ground. Total energy is all kinetic. Kinetic energy has two parts, translational and rotational 1 2 1 2 K mv I w 2 2 Conservation of total energy here requires 11/16/2009 Physics 100 1 2 1 2 mgh mv I w 2 2 35 Displacement Rotation Velocity Angular velocity Acceleration Angular acceleration Mass Moment of inertia Force Torque Momentum Angular momentum Energy Rotational energy 11/16/2009 Physics 100 36