* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Physics 108
Brownian motion wikipedia , lookup
Atomic theory wikipedia , lookup
Fictitious force wikipedia , lookup
Four-vector wikipedia , lookup
Velocity-addition formula wikipedia , lookup
Newton's theorem of revolving orbits wikipedia , lookup
Hamiltonian mechanics wikipedia , lookup
Monte Carlo methods for electron transport wikipedia , lookup
Renormalization group wikipedia , lookup
Center of mass wikipedia , lookup
Routhian mechanics wikipedia , lookup
Old quantum theory wikipedia , lookup
Symmetry in quantum mechanics wikipedia , lookup
Tensor operator wikipedia , lookup
Centripetal force wikipedia , lookup
Relativistic quantum mechanics wikipedia , lookup
Rigid body dynamics wikipedia , lookup
Uncertainty principle wikipedia , lookup
Classical mechanics wikipedia , lookup
Matter wave wikipedia , lookup
Laplace–Runge–Lenz vector wikipedia , lookup
Quantum vacuum thruster wikipedia , lookup
Work (physics) wikipedia , lookup
Specific impulse wikipedia , lookup
Equations of motion wikipedia , lookup
Accretion disk wikipedia , lookup
Theoretical and experimental justification for the Schrödinger equation wikipedia , lookup
Angular momentum wikipedia , lookup
Photon polarization wikipedia , lookup
Classical central-force problem wikipedia , lookup
Angular momentum operator wikipedia , lookup
Relativistic mechanics wikipedia , lookup
Relativistic angular momentum wikipedia , lookup
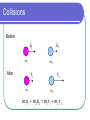
Chapter 8 Impulse and Momentum Momentum and Collisions This chapter is concerned with inertia and motion. Momentum helps us understand collisions. Elastic Collisions - objects rebound Inelastic Collisions - object stick together an usually become distorted and generate heat Momentum Momentum = mass velocity p = mv Momentum is a vector quantity. Large Momentum Examples Huge ship moving at a small velocity P = Mv High velocity bullet P = mv Momentum Examples A large truck has more momentum than a car moving at the same speed because it has a greater mass. Which is more difficult to slow down? The car or the large truck? Impulse Newton’s Second Law can read SF = ma = m(Dv/Dt) = (Dmv)/(Dt) = (Dp/ Dt) Rearranging, Impulse = Dp = FDt When Force is Limited Apply a force for a long time. Examples: Follow through on a golf swing. Pushing a car. F Dt Make it Bounce Dp = p2 - p1 = -p1 - p1 = -2p1 p1 p2 = -p1 Minimize the Force Increase Dt Catching a ball Bungee jumping Dt F Maximize Momentum Change Apply a force for a short time. Examples: Boxing Karate F Dt Conservation of Momentum This means that the momentum doesn’t change. Recall that SF t = D(mv), so SF = 0 In this equation, F is the "external force." Internal forces cannot cause a change in momentum. Examples Example 1: a bullet fired from a rifle Example 2: a rocket in space Collisions Before u1 m1 u2 m2 v1 After m1 v2 m2 m1u1 m2 u 2 m1v1 m2 v2 v = 10 v=0 M M Before Collision p = Mv v’ = 5 M M Mv = 2Mv’ v’ = ½ v After Collision p = 2Mv’ Conserve Energy and Momentum Before Collision Case 1: Equal masses Case 2: M>M Case 3: M<M Coefficient of Restitution v 2 v1 e u 2 u1 For perfectly elastic collisions e = 1. If the two object stick together, e = 0. Otherwise 0 < e < 1. Center of Mass x cm x i mi mi On to problems...