Download Chapter 20_linear mo..

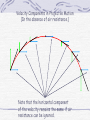
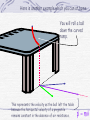
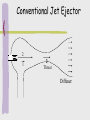
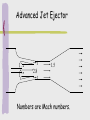
CONSERVATION OF
LINEAR MOMENTUM
Chapter 20
Objectives
Know that linear momentum is conserved
when no outside forces act on the system
Know that linear momentum can be added to
a system by forces, or by adding mass
Know the connection between Newton's laws
and conservation of linear momentum
Be able to do calculations involving linear
momentum
Rat 1
Rat 1
Rat 1
Take 3 minutes to answer the following
(true or false)
1. Mass can be a state quantity.
2. Velocity can be a state quantity.
3. Linear momentum can be a state
quantity.
4. Linear momentum is a vector quantity.
5. Linear momentum is always conserved.
Linear Momentum
Newton developed the concept of linear
momentum.
Linear momentum, p, is defined as the
product of the mass, m, and velocity, v
p=mv


p  mv
The momentum vector is an entirely
different vector than the velocity vector.
Care should be taken in comparing one to
the other.
It is safe to say that the momentum vector
is in the same direction as the velocity
vector as mentioned earlier.
One can also say that the momentum
vector is directly proportional to the
velocity vector, i.e., the momentum vector
doubles if the velocity vector doubles.
But momentum also depends on the mass.
So changing the mass of an object will also
change the momentum vector.
Therefore to change momentum one must
change the mass or velocity or both.
Regardless of what changes, the momentum
vector is always in the same direction as
the velocity vector.


p  mv
As long as there are no external
forces acting on a system of
particles, collisions between the
particles will exhibit conservation of
linear momentum.
This means that the vector sum of
the momenta before collision is equal
to the vector sum of the momenta of
the particles afterwards.


p  mv
This is known as the conservation of
linear momentum.
It is an extremely important concept
in physics.
One important area that makes use of
this conservation principle is
collisions.
This is what you are going to explore
today.


p  mv
The collision you will study will involve two
objects of equal mass colliding in a
horizontal plane and then undergoing
projectile motion after the collision.
Since the horizontal component of velocity
remains constant for a projectile in free
fall, the horizontal part of the projectile
motion can be used to represent the
horizontal component of the momentum
after collision.


p  mv
Simple Examples of Head-On Collisions
(Energy and Momentum are Both Conserved)
Collision between two objects of the same mass. One mass is at rest.
Collision between two objects. One at rest initially has twice the mass.
Collision between two objects. One not at rest initially has twice the mass.


p  mv
Simple Examples of Head-On Collisions
(Totally Inelastic Collision, only Momentum Conserved)
Collision between two objects of the same mass. One mass is at rest.
Collision between two objects. One at rest initially has twice the mass.
Collision between two objects. One not at rest initially has twice the mass.


p  mv
Example of Non-Head-On Collisions
(Energy and Momentum are Both Conserved)
Collision between two objects of the same mass. One mass is at rest.
If you vector add the total momentum after collision,
you get the total momentum before collision.


p  mv
Velocity Components in Projectile Motion
(In the absence of air resistance.)
Note that the horizontal component
of the velocity remains the same if air
resistance can be ignored.
Here is another example which you can at home
You will roll a ball
down the curved
ramp.
This represents the velocity as the ball left the table
because the horizontal velocity of a projectile
remains constant in the absence of air resistance.


p  mv
Linear Momentum
Force is the Rate of Change of Momentum
Mass is a state quantity.
Velocity is also a state quantity, but because
it also has direction, it is also a vector
quantity.
Because mass is a scalar and velocity is a
vector, then momentum is also a vector.
The algebraic combination of state quantities
yields a state quantity, thus momentum is a
state quantity (closed systems only).
Momentum
 Momentum is a property of moving matter.
 Momentum describes the tendency of objects
to keep going in the same direction with the
same speed.
 Changes in momentum result from forces or
create forces.
Momentum
 The momentum of a ball depends on its mass
and velocity.
 Ball B has more momentum than ball A.
Momentum
 The momentum of a ball depends on its mass
and velocity.
 Ball B has more momentum than ball A.
Momentum and Inertia
 Inertia is another property of mass that resists
changes in velocity; however, inertia depends
only on mass.
 Inertia is a scalar quantity.
 Momentum is a property of moving mass that
resists changes in a moving object’s velocity.
 Momentum is a vector quantity.
Momentum




Ball A is 1 kg moving 1m/sec, ball B is 1kg at 3 m/sec.
A 1 N force is applied to deflect the motion of each ball.
What happens?
Does the force deflect both balls equally?
 Ball B deflects much
less than ball A
when the same force
is applied because
ball B had a greater
initial momentum.
Equivalent Momenta
Car: m = 1800 kg; v = 80 m /s
p = 1.44 ·105 kg · m /s
Bus: m = 9000 kg; v = 16 m /s
p = 1.44 ·105 kg · m /s
Train: m = 3.6·104 kg; v = 4 m /s
p = 1.44 ·105 kg · m /s
Kinetic Energy and Momentum
 Kinetic energy and momentum are different quantities,
even though both depend on mass and speed.
 Kinetic energy is a scalar quantity.
 Momentum is a vector, so it always depends on
direction.
Two balls with the same mass and speed have the same kinetic energy
but opposite momentum.
Calculating Momentum
 The momentum of a moving object is its
mass multiplied by its velocity.
 That means momentum increases with both
mass and velocity.
Momentum
(kg m/sec)
Mass (kg)
p=mv
Velocity (m/sec)
Comparing momentum
A car is traveling at a velocity of 13.5 m/sec (30
mph) north on a straight road. The mass of the car
is 1,300 kg. A motorcycle passes the car at a speed
of 30 m/sec (67 mph). The motorcycle (with rider)
has a mass of 350 kg. Calculate and compare the
momentum of the car and motorcycle.
1.
2.
3.
You are asked for momentum.
You are given masses and velocities.
Use: p = m v
4.
5.
Solve for car: p = (1,300 kg) (13.5 m/s) = 17,550 kg m/s
Solve for cycle: p = (350 kg) (30 m/s) = 10,500 kg m/s

The car has more momentum even though it is going much slower.
Conservation of Momentum
 The law of conservation of momentum states
when a system of interacting objects is not
influenced by outside forces (like friction), the
total momentum of the system cannot change.
If you throw a rock forward from a
skateboard, you will move
backward in response.
Conservation of Momentum
Collisions in One Dimension
 A collision occurs when two or more objects hit
each other.
 During a collision, momentum is transferred
from one object to another.
 Collisions can be elastic or inelastic.
Collisions
Elastic collisions
Two 0.165 kg billiard balls roll toward
each other and collide head-on.
Initially, the 5-ball has a velocity of 0.5
m/s.
The 10-ball has an initial velocity of -0.7
m/s.
The collision is elastic and the 10-ball
rebounds with a velocity of 0.4 m/s,
reversing its direction.
What is the velocity of the 5-ball after
the collision?
Elastic
collisions
1.
You are asked for 10-ball’s velocity after collision.
2.
You are given mass, initial velocities, 5-ball’s final velocity.
3.
Diagram the motion, use m1v1 + m2v2 = m1v3 + m2v4
4.
Solve for V3 : (0.165 kg)(0.5 m/s) + (0.165 kg) (-0.7 kg)=
(0.165 kg) v3 + (0.165 kg) (0.4 m/s)
5.
V3 = -0.6 m/s
Inelastic collisions
A train car moving to the right at 10 m/s
collides with a parked train car.
They stick together and roll along the
track.
If the moving car has a mass of 8,000 kg
and the parked car has a mass of 2,000
kg, what is their combined velocity after
the collision?
1.
You are asked for the final velocity.
2.
You are given masses, and initial velocity of moving train
car.
Inelastic collisions
3.
Diagram the problem, use m1v1 + m2v2 = (m1v1 +m2v2) v3
4.
Solve for v3= (8,000 kg)(10 m/s) + (2,000 kg)(0 m/s)
(8,000 + 2,000 kg)
v3= 8 m/s
The train cars moving together to right at 8 m/s.
Collisions in 2 and 3 Dimensions
 Most real-life collisions do not occur in one
dimension.
 In a two or three-dimensional collision, objects
move at angles to each other before or after
they collide.
 In order to analyze two-dimensional collisions
you need to look at each dimension separately.
 Momentum is conserved separately in the x and
y directions.
Collisions in 2 and 3 Dimensions
Force is the Rate of Change of
Momentum
Investigation Key Question:
How are force and momentum
related?
Force is the Rate of Change of
Momentum
 Momentum changes when
a net force is applied.
 The inverse is also true:
 If momentum changes,
forces are created.
 If momentum changes
quickly, large forces are
involved.
Force and Momentum Change
The relationship between force and motion
follows directly from Newton's second law.
Force (N)
Change in momentum
(kg m/sec)
F = D p/D t
Change in time (sec)
Calculating force
Starting at rest, an 1,800 kg rocket takes off, ejecting
100 kg of fuel per second out of its nozzle at a speed of
2,500 m/sec. Calculate the force on the rocket from the
change in momentum of the fuel.
1.
You are asked for force exerted on rocket.
2.
You are given rate of fuel ejection and speed of rocket
3.
Use F = Δp/Δt = (Δm*v) Δt = (Δm/Δt)*v
4.
Thus: F = (Δm/Δt)*v = (100 kg/s)*(-2,500 m/s) = -250,000 N

The fuel exerts and equal and opposite force on rocket of +250,000 N.
Impulse
 The product of a force and
the time the force acts is
called the impulse.
 Impulse is a way to
measure a change in
momentum because it is
not always possible to
calculate force and time
individually since
collisions happen so fast.
Force and Momentum Change
To find the impulse, you rearrange the
momentum form of the second law.
Impulse (N•sec)
FD t=Dp
Change in
momentum
(kg•m/sec)
Impulse can be expressed in kg•m/sec
(momentum units) or in N•sec.
Jet Engines
 Nearly all modern airplanes use jet propulsion to fly. Jet engines
and rockets work because of conservation of linear momentum.
 A rocket engine uses the same principles as a jet, except that in
space, there is no oxygen.
 Most rockets have to carry so much oxygen and fuel that the
payload of people or satellites is usually less than 5 percent of
the total mass of the rocket at launch.
Momentum and Energy

Two objects with masses m1 and m2
have equal kinetic energy. How do the
magnitudes of their momenta
compare?
(A) p1 < p2
(B) p1 = p2
(C) p1 > p2
(D) Not enough information is given
May 22, 2017
Linear Momentum and Newton’s
Laws
Newton’s 1st law
When viewed in an inertial reference frame*,
an object either remains at rest or moves
at a constant velocity, unless acted upon
by an external force
Therefore, if there is no force acting on a
body, its momentum stays constant.
*Recall Coriolis and centrifugal forces
Newton’s 2nd law
The second law states that the net force on
an object is equal to the rate of change
(that is, the derivative) of its linear
momentum p in an inertial reference frame
F = dp/dt = d(mv)/dt
For constant-mass systems, mass can be
taken outside the differentiation operator
F = mdv/dt = ma
Linear Momentum and Newton’s
Laws
Newton’s 3rd law
The linear momentum of one body changes
the same as the other body, but in
opposite directions, so the linear
momentum of the universe is not affected.
Forces always exist by the interaction of
bodies; the force on one body is equal and
opposite to the force on the other body.
Newton’s third law
States that all forces exist in pairs:
if one object A exerts a force FA on a second object B,
then B simultaneously exerts a force FB on A,
and the two forces are equal and opposite: FA = −FB.
The third law means that all forces are interactions
between different bodies,
and thus that there is no such thing as a unidirectional
force or a force that acts on only one body.
This law is sometimes referred to as the action-reaction
law. The action and the reaction are simultaneous,
It does not matter which is called the action and which is
called reaction;
Both forces are part of a single interaction, and neither
force exists without the other.
Newton stated the third law within a world-view
Assumed instantaneous action at a distance between
material particles.
However, he was prepared for philosophical criticism
of this action at a distance, and it was in this context
that he stated the famous phrase "I feign no
hypotheses".
In modern physics, action at a distance has been
completely eliminated, except for effects involving
quantum entanglement.
However in modern engineering in all practical
applications involving the motion of vehicles and
satellites, the concept of action at a distance is used
extensively.
Revisiting the UAE
Before applying the Universal Accounting
Equation (UAE):
Define a system.
Determine what quantity will be counted.
Define time interval for counting.
Best for Energy, Mass, …
Care should be taken for Charge,
Momentum, …
Designating the System
When solving linear momentum problems,
the system boundary must be defined.
This boundary is at the discretion of the
engineer.
There is no requirement that the system
contain all bodies involved in the process.
Thus, a system can have unbalanced forces
which will change the linear momentum of the
system.
Revisiting the UAE
The UAE equation
FINAL - INITIAL = IN - OUT + GEN - CONS
Accum = Net Input + Net Generation
State
Path
Terms of the UAE
FINAL AMOUNT: …in system at the END of time period
INITIAL AMOUNT: …in system at the START of time
period
INPUT: …PASSING through boundary INTO system
during time period
OUTPUT: …PASSING through boundary OUT of
system during time period
GENERATION: …PRODUCED during time period within
boundary
CONSUMPTION: …DESTROYED during time period
within boundary
Linear Momentum Is Conserved
Linear momentum when is a conserved
quantity:
0
0
FINAL - INITIAL = IN - OUT + GEN - CONS
0
Accum = Net Input + Net Generation
Steps to Applying the UAE
To use the UAE, define the system, then compute:
1. INITIAL linear momentum for the mass in the
system,
2. FINAL linear momentum for the mass in the
system,
3. Linear momentum INPUT into the system,
4. Linear momentum OUTPUT from the system.
Linear Momentum Change
There are two main ways that the linear
momentum of a system can change:
mass changes
velocity changes
a combination of both: external forces
Otherwise, the accumulation of linear
momentum is zero
Changing Linear Momentum by
External Forces
-F
F
Initial State
mvi
Positive Direction
Time Passes
F
Final State
mvf
-F
Changing Linear Momentum by
Unbalanced Forces
Momentum flow INTO or OUT OF a
system can result from FORCES.
Mathematically,
SI Units of Force = kg·m/s2
SI Units of Momentum = kg·m/s
Thus, Units of Force = Units of Momentum/s
p  F
Analogy: Mass Flowing into Tank
Assume mass flow rates are constant
Dt
m in
m out m in
Dmsystem  m final  minitial  min  mout  mnet
Dmsystem
 m in  m out  m net
Dt
dmsys
 m net
dt
m out
Analogy: Momentum Flowing from
Force
dmsys
dt
dpsys
dt
 m net
(From previous slide)
(By analogy)
 p net  Fnet
d ( mv )
dv  ma  F
m

net
dt
dt
Fnet  ma
(For constant mass in system)
Newton' s 2nd Law! !!
Individual Exercise #1:
A 1.000-ton dragster has a jet engine that
provides a thrust of 3000. lbf. The
dragster starts from a dead stop at the
start line and crosses the finish line 9
seconds later. Neglect mass loss.
(a) What is its final velocity?
(b) How long was the track?
Pairs Exercise #1
A 0.100-kg hockey puck is stationary on the ice.
Then it is hit with a hockey stick and 0.020 s
later, the puck is traveling at 100. km/h.
(a) What is the average force (N) on the puck?
(b) What is the average force (N) on the hockey
stick?
Linear Momentum Change by
Mass Transfer
Suppose you define a system that contains a
single object of mass m1 moving at a velocity
of v1 in the positive x-direction
As time passes, two more objects enter the
system with masses m2 and m3 and velocities
v2 and v3 respectively, also in the x-direction.
Time m2v2
m1v1
Passes
m3v3
m1v1
Time
Passes
system
boundary
m2v2
m1v1
m3v3
Linear Momentum Change by
Mass Transfer
Initial linear momentum
pi = m1v1
Final linear momentum
pf = (m1v1 + m2v2 + m3v3)
Note:for this case we can write these as scalars if we
use the magnitude of the x-component of the vectors.
Then, accumulation = pf - pi is not zero.
Pairs Exercise #2
A 1.0-ton (including ammo and pilot)
military helicopter is flying at 40 mph. It
has a machine gun that fires 60 bullets
per second in the forward direction.
Each 0.5-lbm bullet exits the gun at 1800
mph. After a 2-s burst of fire, what is
the helicopter speed?
Pairs Exercise #3
For the previous exercise, if the final
system had been defined to include the
fired bullets, would the answer be
different?
Helicopter
w/ ammo
mi = 1 ton
vi = 40 mph
Initial
Helicopter
w/ less ammo
mf = ?
vf = ?
Final
bullets
Systems Without Net Linear
Momentum Input
No unbalanced forces & no mass transfer
into or out of the system.
UAE simplifies to:
ACCUMULATION=0
FINAL AMOUNT - INITIAL AMOUNT = 0
FINAL AMOUNT = INITIAL AMOUNT
Therefore, there is no change in
linear momentum of the system.
Individual Exercise #2
A 5.0-g bullet is fired horizontally at 300
m/s and passes through a 500-g block of
wood initially at rest on a frictionless
surface. The bullet emerges with a speed
of 100 m/s. What is the final speed of the
block?
Pairs Exercise #4:
In Example 20.5, what is the change in
linear momentum of the white ball? The
black ball? What is the total kinetic
energy of the two balls before the impact
and after the impact? Is energy
conserved in this impact?
ary, so Equation 20-24 may be used.
(20-24)
Pairs Exercise #5.1
The following two streams of steam are blended together.
Stream A: 1 kg, 1 m/s
Stream B: 1 kg, 10 m/s
a. What is the mass of the blended stream?
b. Assuming no friction, what is the final velocity of the
blended stream?
c. What is the kinetic energy before, and after, the blending
process?
d. What is the efficiency, i.e., what fraction of the original
kinetic energy is retained in the blended stream?
Conventional Jet Ejector
2
1
3
Throat
Diffuser
Pairs Exercise #5.2
The following two streams of steam are blended together.
Stream A: 1 kg, 1 m/s
Stream B: 1 kg, 2 m/s
a. What is the mass of the blended stream?
b. Assuming no friction, what is the final velocity of the
blended stream?
c. What is the kinetic energy before, and after, the blending
process?
d. What is the efficiency, i.e., what fraction of the original
kinetic energy is retained in the blended stream?
Advanced Jet Ejector
1
1
1
2.8
1
1.5
Numbers are Mach numbers.
QUESTION 1:
For years, space travel was believed to be impossible
because there was nothing that rockets could push off of in
space in order to provide the propulsion necessary to
accelerate. This inability of a rocket to provide propulsion is
because ...
a) space is void of air so the rockets have nothing to push
off of.
b) gravity is absent in space.
c) space is void of air and so there is no air resistance in
space.
d) nonsense! Rockets do accelerate in space and have been
able to do so for a long time.
Question 2
While driving down the road, a firefly strikes
the windshield of a bus and makes a quite
obvious mess in front of the face of the
driver.
This is a clear case of Newton's third law of
motion: the firefly hits the bus and the bus
hits the firefly.
Which of the two forces is greater:
(a) the force on the firefly
(b) the force on the bus
(c) none of the above
QUESTION 3: In the top picture (below), Joe is pulling upon
a rope that is attached to a wall. In the bottom picture, Joe is
pulling upon a rope that is attached to an elephant. In each
case, the force scale reads 500 Newton. Joe is pulling ...
a) with more force when the rope is attached to the wall.
b) with more force when the rope is attached to the elephant.
c) the same force in each case