* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Ch13-2 Simple Harmonic Motion
Specific impulse wikipedia , lookup
N-body problem wikipedia , lookup
Classical mechanics wikipedia , lookup
Velocity-addition formula wikipedia , lookup
Statistical mechanics wikipedia , lookup
Relativistic mechanics wikipedia , lookup
Brownian motion wikipedia , lookup
Work (physics) wikipedia , lookup
Jerk (physics) wikipedia , lookup
Rigid body dynamics wikipedia , lookup
Thermodynamic system wikipedia , lookup
Classical central-force problem wikipedia , lookup
Seismometer wikipedia , lookup
Newton's laws of motion wikipedia , lookup
Centripetal force wikipedia , lookup
History of fluid mechanics wikipedia , lookup
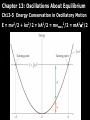
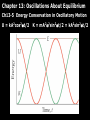
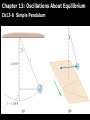
Chapter 13: Oscillations About Equilibrium Whenever F = -kx or U(x) is a parabola F = -kx U = kx2/2 Chapter 13: Oscillations About Equilibrium Ch13-1 Periodic Motion T = period – the time for one cycle or repeat time f = frequency – the number of cycles per second f = 1/T = angular frequency – radians per second = 2f = 2/T Don’t confuse angular frequency with angular velocity. Chapter 13: Oscillations About Equilibrium Ch13-2 Simple Harmonic Motion (SHM) Chapter 13: Oscillations About Equilibrium Ch13-2 Simple Harmonic Motion (SHM) Displaying Position Versus Time for Simple Harmonic Motion x = Acos(2t/T) t=0 Chapter 13: Oscillations About Equilibrium Ch13-2 Simple Harmonic Motion (SHM) Simple Harmonic Motion as a Sine or a Cosine Chapter 13: Oscillations About Equilibrium Ch13-2 Simple Harmonic Motion (SHM) P13.8 (p.425) CT1: A mass attached to a spring oscillates back and forth as indicated in the position vs. time plot below. At point P, the mass has A. positive velocity and positive acceleration. B. positive velocity and negative acceleration. C. positive velocity and zero acceleration. D. negative velocity and positive acceleration. E. negative velocity and negative acceleration. F. negative velocity and zero acceleration. G. zero velocity but is accelerating (positively or negatively). H. zero velocity and zero acceleration. CT2: A mass suspended from a spring is oscillating up and down as indicated. Consider two possibilities: (i) at some point during the oscillation the mass has zero velocity but is accelerating (positively or negatively); (ii) at some point during the oscillation the mass has zero velocity and zero acceleration. A. Both occur sometime during the oscillation. B. Neither occurs during the oscillation. C. Only (i) occurs. D. Only (ii) occurs. Chapter 13: Oscillations About Equilibrium Ch13-3 Connections Between Uniform Circular Motion and SHM Chapter 13: Oscillations About Equilibrium Ch13-3 Connections Between Uniform Circular Motion and SHM Position Versus Time in Simple Harmonic Motion Chapter 13: Oscillations About Equilibrium Ch13-3 Connections Between Uniform Circular Motion and SHM Velocity Versus Time in Simple Harmonic Motion Chapter 13: Oscillations About Equilibrium Ch13-3 Connections Between Uniform Circular Motion and SHM Acceleration Versus Time in Simple Harmonic Motion Chapter 13: Oscillations About Equilibrium Ch13-3 Connections Between Uniform Circular Motion and SHM P13.22 (p.425) P13.66 (p.428) Chapter 13: Oscillations About Equilibrium Ch13-4 The Period of a Mass on a Spring P13.63 (p.427) P13.31 (p.426) k m1 Factors Affecting the Motion of a Mass on a Spring Chapter 13: Oscillations About Equilibrium Ch13-5 Energy Conservation in Oscillatory Motion E = mv2/2 + kx2/2 = kA2/2 = mvmax2/2 = mA22/2 Chapter 13: Oscillations About Equilibrium Ch13-5 Energy Conservation in Oscillatory Motion U = kA2cos2t/2 K = mA22sin2t/2 = kA2sin2t/2 Chapter 13: Oscillations About Equilibrium Ch13-5 Energy Conservation in Oscillatory Motion P13.67 (p.428) CT3: In P13.67b, which principle do we have to use to get the speed of the bob and bullet right after the collision? A. Newton’s laws. B. Conservation of energy. C. Conservation of momentum. D. The work-kinetic energy theorem. CT4: In P12.67b, which principle do we have to use to get the speed of the bullet from the height the bob rises? A. Newton’s laws. B. Conservation of energy. C. Conservation of momentum. D. The work-kinetic energy theorem. Chapter 13: Oscillations About Equilibrium Ch13-6 Simple Pendulum r t Chapter 13: Oscillations About Equilibrium Ch13-6 Simple Pendulum P13.67c (p.428) CT5: In P13.52a the acceleration of gravity at the surface of the Moon is one-sixth that at the surface of the Earth. If the pendulum were taken to the Moon, the period will A. increase. B. decrease. C. stay the same. Simple Pendulum: Energy View Chapter 13: Oscillations About Equilibrium Ch13-7 Damped Oscillations Chapter 13: Oscillations About Equilibrium Ch13-7 Damped Oscillations Chapter 13: Oscillations About Equilibrium Ch13-8 Driven Oscillations and Resonance