* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Chapter 19 Outline The First Law of Thermodynamics
Analytical mechanics wikipedia , lookup
Modified Newtonian dynamics wikipedia , lookup
N-body problem wikipedia , lookup
Theoretical and experimental justification for the Schrödinger equation wikipedia , lookup
Routhian mechanics wikipedia , lookup
Old quantum theory wikipedia , lookup
Classical mechanics wikipedia , lookup
Newton's theorem of revolving orbits wikipedia , lookup
Center of mass wikipedia , lookup
Electromagnetic mass wikipedia , lookup
Jerk (physics) wikipedia , lookup
Hooke's law wikipedia , lookup
Brownian motion wikipedia , lookup
Relativistic mechanics wikipedia , lookup
Work (physics) wikipedia , lookup
Rigid body dynamics wikipedia , lookup
Centripetal force wikipedia , lookup
Classical central-force problem wikipedia , lookup
Hunting oscillation wikipedia , lookup
Newton's laws of motion wikipedia , lookup
Seismometer wikipedia , lookup
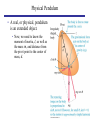
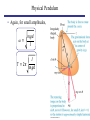
Chapter 14 Outline Periodic Motion • Oscillations • Amplitude, period, frequency • Simple harmonic motion • Displacement, velocity, and acceleration • Energy in simple harmonic motion • Pendulums • Simple • Physical • Damped oscillations • Resonance Periodic Motion • Many types of motion repeat again and again. • Plucked string on a guitar, a child in a swing, sound waves in a flute… • This is called periodic motion, or oscillation. • Stable equilibrium point • Displacement from equilibrium leads to a force (or torque) to return it to equilibrium. • Kinetic energy leads to overshoot, causing repeat Periodic Motion Notation • Amplitude – The maximum magnitude of displacement from equilibrium • Period, 𝑇 – The time for one cycle (s) • Frequency, 𝑓 – Number of cycle per unit time (Hz = 1/s) • Angular frequency, 𝜔 – Equal to 2𝜋𝑓 (rad/s) • From these definitions, 𝑓= 1 , 𝑇 and 𝑇 = 1 𝑓 Simple Harmonic Motion • If the restoring force is directly proportional to the displacement, the resulting oscillation is simple harmonic motion. • One example is a mass on spring that obeys Hooke’s law. 𝐹 = −𝑘𝑥 Mass on a Spring • Using Newton’s second law, in one dimension, 𝐹 = −𝑘𝑥 = 𝑚𝑎 𝑘 𝑎=− 𝑥 𝑚 • Since acceleration is the second time derivative of position, 𝑑2𝑥 𝑘 =− 𝑥 2 𝑑𝑡 𝑚 Mass on a Spring • Sinusoidal functions satisfy this differential equation. 𝑥 = 𝐴 cos(𝜔𝑡 + 𝜙) • Plugging this into the equation, we can solve for 𝜔, 𝑑𝑥 = −𝜔𝐴 sin(𝜔𝑡 + 𝜙) 𝑑𝑡 𝑑2𝑥 2 𝐴 cos 𝜔𝑡 + 𝜙 = −𝜔 2 𝑥 = −𝜔 𝑑𝑡 2 • Comparing to 𝑑2𝑥 𝑑𝑡 2 =− 𝑘 𝑥, 𝑚 𝜔= 𝑘 𝑚 Simple Harmonic Motion of a Mass on a Spring • Angular frequency 𝜔= 𝑘 𝑚 • Frequency 1 𝑘 𝑓= 2𝜋 𝑚 • Period 𝑚 𝑇 = 2𝜋 𝑘 • Amplitude does not enter the equations as long as the spring obeys Hooke’s law. (Generally for small amplitudes.) Displacement, Velocity and Acceleration • As we saw earlier, sinusoidal functions satisfy the differential equation for simple harmonic motion. 𝑥 = 𝐴 cos(𝜔𝑡 + 𝜙) • 𝐴 is the amplitude, and 𝜙 is the phase angle (starting position) • We find the velocity at any time by taking the time derivative, 𝑑𝑥 𝑣= = −𝜔𝐴 sin(𝜔𝑡 + 𝜙) 𝑑𝑡 • Likewise, for the acceleration, 𝑑2𝑥 𝑎 = 2 = −𝜔2 𝐴 cos 𝜔𝑡 + 𝜙 𝑑𝑡 SHM Example Energy in Periodic Motion • If there are no dissipative forces (friction), the total energy is constant. 1 1 2 1 2 2 𝐸 = 𝑚𝑣 + 𝑘𝑥 = 𝑘𝐴 = constant 2 2 2 Energy Plots in Periodic Motion 1 1 2 2 𝐸 = 𝐾 + 𝑈 = 𝑚𝑣 + 𝑘𝑥 2 2 Vertical SHM • We looked at a mass oscillating horizontally on a frictionless table. • How does this change if the mass is hanging vertically? • The equilibrium point will not be at the same extension of the spring. (∆𝑙 instead of 0) 𝑘∆𝑙 = 𝑚𝑔 𝐹net = 𝑘 ∆𝑙 − 𝑥 − 𝑚𝑔 = 𝑘∆𝑙 − 𝑚𝑔 − 𝑘𝑥 𝐹net = −𝑘𝑥 • This the same as before, but 𝑥 is measured from the new equilibrium position. Molecular Vibrations • Interactions between neutral atoms can be described by the Lennard-Jones potential. 𝑅0 12 𝑅0 6 𝑈 = 𝑈0 −2 𝑟 𝑟 • The positive term is due to the Pauli repulsion. • The negative, is due to long range attractive forces (LDF). • This does not look like the simple parabolic potential well from a mass on a spring, but we can still look at the oscillations. Molecular Vibrations • The restoring force is: 𝑑𝑈 𝑈0 𝐹𝑟 = − = 12 𝑑𝑟 𝑅0 𝑅0 𝑟 13 𝑅0 − 𝑟 7 • Using, the binomial theorem, 𝑛 𝑛−1 2 𝑛 1 + 𝑢 = 1 + 𝑛𝑢 + 𝑢 +⋯ 2! • For small oscillations, the restoring force reduces to: 72𝑈0 𝐹𝑟 = − 𝑥 2 𝑅0 • Where 𝑥 = 𝑟 − 𝑅0 • This is now Hooke’s law. Simple Pendulum • The simplest pendulum is a point mass on a massless string. • What provides the restoring force? • How can we describe the motion? • Mass 𝑚, length 𝐿. Simple Pendulum • For small amplitudes, 𝜔= 𝑔 𝐿 𝜔 1 𝑔 𝑓= = 2𝜋 2𝜋 𝐿 1 𝐿 𝑇 = = 2π 𝑓 𝑔 Physical Pendulum • A real, or physical, pendulum is an extended object. • Now, we need to know the moment of inertia, 𝐼, as well as the mass 𝑚, and distance from the pivot point to the center of mass, 𝑑. Physical Pendulum • Again, for small amplitudes, 𝜔= 𝑚𝑔𝑑 𝐼 𝐼 𝑇 = 2π 𝑚𝑔𝑑 Physical Pendulum Example Damped Oscillations • We have assumed there was no friction, and therefore the amplitude never decreases, but in reality, energy will be lost to friction. • This decrease in amplitude is damping. • Consider the simplest case where the frictional damping is proportional to the velocity of the object. Σ𝐹 = −𝑘𝑥 − 𝑏𝑣 • This force always opposes the motion. −𝑘𝑥 − 𝑏𝑣 = 𝑚𝑎 𝑑𝑥 𝑑2𝑥 −𝑘𝑥 − 𝑏 =𝑚 2 𝑑𝑡 𝑑𝑡 Underdamped Oscillations • Solving this differential equation for small 𝑏, 𝑥 = 𝐴𝑒 − 𝑏/2𝑚 𝑡 cos(𝜔′ 𝑡 + 𝜙) • This is very similar to simple harmonic motion but with an exponentially decreasing amplitude. • Also, the angular frequency is decreased. 𝜔′ = 𝑘 𝑏2 − 𝑚 4𝑚2 Critical and Over-damped Oscillations • When the equation for 𝜔′ = 0, 𝑏 = 2 𝑘𝑚 • The system is critically damped, and it no longer oscillates, but returns exponentially to equilibrium. • If 𝑏 > 2 𝑘𝑚, the system is overdamped, and it decays to zero with a double exponential. Forced Oscillations and Resonance • If the system is driven at some arbitrary frequency, there will not be much of a response. • But, if it is driven near the natural resonance frequency, the response can be quite large. Chapter 14 Summary Periodic Motion • Oscillations • Amplitude, 𝐴 • Period, 𝑇 = 1 𝑓 • Frequency, 𝑓, and angular frequency, 𝜔 = 2𝜋𝑓 • Simple harmonic motion – Spring: 𝜔 = 𝑘 𝑚 • 𝑥 = 𝐴 cos(𝜔𝑡 + 𝜙) • 𝑣= 𝑑𝑥 𝑑𝑡 • 𝑎= 𝑑2 𝑥 𝑑𝑡 2 = −𝜔𝐴 sin(𝜔𝑡 + 𝜙) = −𝜔2 𝐴 cos 𝜔𝑡 + 𝜙 • Energy in simple harmonic motion 1 1 2 1 2 2 𝐸 = 𝑚𝑣 + 𝑘𝑥 = 𝑘𝐴 = constant 2 2 2 Chapter 14 Summary Periodic Motion • Pendulums • Simple: 𝜔 = 𝑔 𝐿 • Physical: 𝜔 = 𝑚𝑔𝑑 𝐼 • Damped oscillations • 𝑥 = 𝐴𝑒 − 𝑏/2𝑚 𝑡 cos(𝜔′ 𝑡 + 𝜙) • 𝜔′ = 𝑘 𝑚 − 𝑏2 4𝑚2 • Resonance – driven near 𝜔′