* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Lecture18-11
N-body problem wikipedia , lookup
Hooke's law wikipedia , lookup
Classical mechanics wikipedia , lookup
Specific impulse wikipedia , lookup
Modified Newtonian dynamics wikipedia , lookup
Atomic theory wikipedia , lookup
Jerk (physics) wikipedia , lookup
Brownian motion wikipedia , lookup
Mass in special relativity wikipedia , lookup
Classical central-force problem wikipedia , lookup
Mass versus weight wikipedia , lookup
Center of mass wikipedia , lookup
Centripetal force wikipedia , lookup
Newton's laws of motion wikipedia , lookup
Equations of motion wikipedia , lookup
Electromagnetic mass wikipedia , lookup
Hunting oscillation wikipedia , lookup
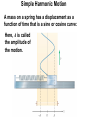
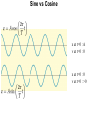
Lecture 18 – Oscillations about Equilibrium Periodic Motion Period: time required for one cycle of periodic motion Frequency: number of oscillations per unit time This unit is called the Hertz: Simple Harmonic Motion A spring exerts a restoring force that is proportional to the displacement from equilibrium: Displaced, at rest Moving, past equilibrium point Displaced, at rest Moving, past equilibrium point Displaced, at rest This is called “Simple Harmonic Motion” Simple Harmonic Motion A mass on a spring has a displacement as a function of time that is a sine or cosine curve: Here, A is called the amplitude of the motion. Simple Harmonic Motion If we call the period of the motion T – this is the time to complete one full cycle – we can write the position as a function of time: Time Position t =0 x=A t=T x = Acos(2π) = A t = T/2 x = Acos(π) = -A T t = T/4 x = Acos(π/2) = 0 The position at time t +T is the same as the position at time t, as we would expect. Sine vs Cosine x at t=0 : A v at t=0 : 0 x at t=0 : 0 v at t=0 : >0 Harmonic Motion I A mass on a spring in SHM has amplitude A and period T. What is the total distance traveled by the mass after a time interval T? a) 0 b) A/2 c) A d) 2A e) 4A Harmonic Motion I A mass on a spring in SHM has amplitude A and period T. What is the total distance traveled by the mass after a time interval T? a) 0 b) A/2 c) A d) 2A e) 4A In the time interval T (the period), the mass goes through one complete oscillation back to the starting point. The distance it covers is A + A + A + A = (4A). Harmonic Motion II A mass on a spring in SHM has amplitude A and period T. What is the net displacement of the mass after a time interval T? a) 0 b) A/2 c) A d) 2A e) 4A Harmonic Motion II A mass on a spring in SHM has amplitude A and period T. What is the net displacement of the mass after a time interval T? a) 0 b) A/2 c) A d) 2A e) 4A The displacement is x = x2 – x1. Because the initial and final positions of the mass are the same (it ends up back at its original position), then the displacement is zero. Follow-up: What is the net displacement after a half of a period? The Pendulum A simple pendulum consists of a mass m (of negligible size) suspended by a string or rod of length L (and negligible mass). The angle it makes with the vertical varies with time as a sine or cosine. How a pendulum is like the mass on a spring Looking at the forces on the pendulum bob, we see that the restoring force is proportional to sin θ The restoring force for a spring is proportional to the displacement This is the condition for simple harmonic motion Approximation for sin θ However, for small angles, sin θ and θ are approximately equal. θ (deg) θ (rad) sin(θ) 1 0.01745 0.01745 5 0.08727 0.08716 10 0.1745 0.1736 20 0.3491 0.3420 Pendulum for small angles = simple harmonic for small angles of the pendulum bob, the restoring force is proportional to θ F = -mg θ = -mg s / L The restoring force for a spring is proportional to the displacement F= -kx So: the motion of the angle of the pendulum is the same as the motion for the mass on a spring, with k mg/L Uniform Circular Motion and Simple Harmonic Motion An object in simple harmonic motion has the same motion as one component of an object in uniform circular motion Assume oscillation of mass on the spring has the same period T as the circular motion of the peg on the “record player” Position of Peg in Circular Motion Here, the object in circular motion has an angular speed of: where T is the period of motion of the object in simple harmonic motion. The position as a function of time: ... just like the simple harmonic motion! Velocity of Peg in Circular Motion Linear speed v = Aω x component: Acceleration of Peg in Circular Motion Linear acceleration a = Aω2 x component: Summary of Simple Harmonic Motion The position as a function of time: From this comparison with circular motion, we can see: The angular frequency: The velocity as a function of time: The acceleration as a function of time: Speed and Acceleration A mass on a spring in SHM has a) x = A amplitude A and period T. At b) x > 0 but x < A what point in the motion is v = 0 c) x = 0 and a = 0 simultaneously? d) x < 0 e) none of the above Speed and Acceleration A mass on a spring in SHM has a) x = A amplitude A and period T. At b) x > 0 but x < A what point in the motion is v = 0 c) x = 0 and a = 0 simultaneously? d) x < 0 e) none of the above If both v and a were zero at the same time, the mass would be at rest and stay at rest! Thus, there is NO point at which both v and a are both zero at the same time. Follow-up: Where is acceleration a maximum? The Period of a Mass on a Spring For the mass on a spring: Substituting the time dependencies of a and x gives and the period is: The Period of a Mass on a Spring Vertical Spring Fs=kx What if the mass hangs from a vertical spring? new equilibrium position: x= -d = -mg/k total force as a function of x: d x=0 x=-d W=mg with Looks like the same spring, with a different equilibrium position (x’=0 -> x = -d) Simple harmonic motion is unchanged from the horizontal case! Energy Conservation in Oscillatory Motion In an ideal system with no nonconservative forces, the total mechanical energy is conserved. For a mass on a spring: Since we know the position and velocity as functions of time, we can find the maximum kinetic and potential energies: Energy Conservation in Oscillatory Motion As a function of time, So the total energy is constant; as the kinetic energy increases, the potential energy decreases, and vice versa. 0 Period of a Pendulum A pendulum is like the mass on a spring, with k=mg/L Therefore, we find that the period of a pendulum depends only on the length of the string: Physical Pendula A physical pendulum is a solid mass that oscillates around its center of mass, but cannot be modeled as a point mass suspended by a massless string. Examples: Period of a Physical Pendulum In this case, it can be shown that the period depends on the moment of inertia: Substituting the moment of inertia of a point mass a distance l from the axis of rotation gives, as expected: Damped Oscillations In most physical situations, there is a nonconservative force of some sort, which will tend to decrease the amplitude of the oscillation, and which is typically proportional to the speed: This causes the amplitude to decrease exponentially with time: Damped Oscillations This exponential decrease is shown in the figure: “underdamped” means that there is more than one oscillation Damped Oscillations The previous image shows a system that is underdamped – it goes through multiple oscillations before coming to rest. A critically damped system is one that relaxes back to the equilibrium position without oscillating and in minimum time; an overdamped system will also not oscillate but is damped so heavily that it takes longer to reach equilibrium. Driven Oscillations and Resonance An oscillation can be driven by an oscillating driving force; the frequency of the driving force may or may not be the same as the natural frequency of the system. Driven Oscillations and Resonance If the driving frequency is close to the natural frequency, the amplitude can become quite large, especially if the damping is small. This is called resonance. Energy in SHM I A mass on a spring oscillates in simple harmonic motion with amplitude A. If the mass is doubled, but the amplitude is not changed, what will happen to the total energy of the system? a) total energy will increase b) total energy will not change c) total energy will decrease Energy in SHM I A mass on a spring oscillates in simple harmonic motion with amplitude A. If the mass is doubled, but the amplitude is not changed, what will happen to the total energy of the system? a) total energy will increase b) total energy will not change c) total energy will decrease The total energy is equal to the initial value of the elastic potential energy, which is PEs = kA2. This does not depend on mass, so a change in mass will not affect the energy of the system. Follow-up: What happens if you double the amplitude? Spring on the Moon A mass oscillates on a vertical spring with period T. If the whole setup is taken to the Moon, how does the period change? a) period will increase b) period will not change c) period will decrease Spring on the Moon A mass oscillates on a vertical spring with period T. If the whole setup is taken to the Moon, how does the period change? a) period will increase b) period will not change c) period will decrease The period of simple harmonic motion depends only on the mass and the spring constant and does not depend on the acceleration due to gravity. By going to the Moon, the value of g has been reduced, but that does not affect the period of the oscillating mass–spring system.