Download Musical Scales and Tonality - University of Toronto Scarborough

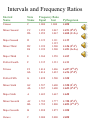
Musical Systems
•
Facts about musical systems
• Musical cultures make use of variation
in pitch
• Use tones of low to high frequency,
and combine them in various ways
• Pitch and frequency are continuous
scales
• Yet musical cultures use discrete
pitches
• Use of discrete pitches, as opposed
to continuously varying pitches, a
universal
• Although there is potentially a large set,
we don’t actually use the entire set
• Octave equivalence – repeat “notes”
with 2:1 frequency ratio
• Collapse across octaves, have 12
distinct tones – called chromatic set
Musical Scales
The Chromatic Scale
C C# D D# E F F# G G# A A# B C
Db
Eb
Gb
Ab
Bb
Note Names:
“C” “D”
“E” “F” “G” “A” “B”
“C Sharp” “D Sharp” “F Sharp” “G Sharp” “A Sharp”
“D Flat” “E Flat” “G Flat” “A Flat” “B Flat”
Difference: 1 Semitone
┌─┐┌─┐
C C# D D# E
F F# G G# A A# B
└───┘└───┘
Difference: 2 Semitones
C
Musical Systems
•
Chromatic Set
• Octave equivalence
• Tones with 2:1 frequency ratio have
the same note name
• Twelve equally divided logarithmic
intervals
• Produces 12 equal steps within the
octave
• Calculated by multiplying each
frequency by 21/12, or 1.059
Intervals and Frequency Ratios
Interval
Name
Note
Name
Frequency Ratio
Equal
Unison
C
1.000
Minor Second
C#
Db
1.059
1.059
Major Second
D
1.122
Minor Third
D#
Eb
1.189
1.189
Major Third
E
1.260
Perfect Fourth
F
1.335
Tritone
F#
Gb
1.414
1.414
Perfect Fifth
G
1.498
Minor Sixth
G#
Ab
1.587
1.587
Major Sixth
A
1.682
Minor Seventh
A#
Bb
1.782
1.782
Major Seventh
B
1.888
Octave
C
2.000
Musical Systems
•
Is the division of the octave into 12 steps a
norm?
• The use of quartertones (24 steps to the
octave)
• First proposed in West in 19th
century, uses freq ratio of 21/24
• http://www.youtube.com/watch?v=
Nxrfoar3HfQ
• Karl Stockhausen
• Works using 7 – 60 steps per octave
• Classical Indian music
• 22 notes per octave
• Basic structure same as 12 tone
Western system, though
• Arab Persian music
• 15-24 steps per octave
• Scales not played microtonally,
though
Tuning Systems
•
Consonance vs. Dissonance
• Roughly defined by freq ratio between
notes
• Smaller frequency ratios are more
consonant
• How well do two notes go together?
• What are some consonant frequency
ratios?
• 2:1 – Octave
• 3:2 – Musical fifth
Intervals and Frequency Ratios
Interval
Name
Note
Name
Frequency Ratio
Equal
Just
Unison
C
1.000
1.000
Minor Second
C#
Db
1.059
1.059
1.067
1.067
Major Second
D
1.122
Minor Third
D#
Eb
1.189
1.189
1.111 (10:9)
1.125 (9:8)
1.200
1.200
Major Third
E
1.260
1.250
Perfect Fourth
F
1.335
1.333
Tritone
F#
Gb
1.414
1.414
1.406 (45:32)
1.422 (64:45)
Perfect Fifth
G
1.498
1.500
Minor Sixth
G#
Ab
1.587
1.587
1.600
1.600
Major Sixth
A
1.682
1.667
Minor Seventh
A#
Bb
1.782
1.782
1.777
1.800
Major Seventh
B
1.888
1.875
Octave
C
2.000
2.000
Intervals and Frequency Ratios
Interval
Name
Note
Name
Frequency Ratio
Equal
Just
Pythagorean
Unison
C
1.000
1.000
1.000
Minor Second
C#
Db
1.059
1.059
1.067
1.067
1.053 (28:35)
1.068 (37:211)
Major Second
D
1.122
1.125
Minor Third
D#
Eb
1.189
1.189
1.111
1.125
1.200
1.200
Major Third
E
1.260
1.250
1.265
Perfect Fourth
F
1.335
1.333
1.333
Tritone
F#
Gb
1.414
1.414
1.406
1.422
1.407 (210:36)
1.424 (36:29)
Perfect Fifth
G
1.498
1.500
1.500
Minor Sixth
G#
Ab
1.587
1.587
1.600
1.600
1.580 (27:34)
1.602 (38:212)
Major Sixth
A
1.682
1.667
1.688
Minor Seventh
A#
Bb
1.782
1.782
1.777
1.800
1.788 (24:32)
1.802 (310:215)
Major Seventh
B
1.888
1.875
1.900
Octave
C
2.000
2.000
2.000
1.186 (25:33)
1.201 (39:214)
Musical Tonality
•
Tonality:
• One note functions as a reference point
for all of the tones
• Called the “tonic” or “tonal center”
• Other pitches have well-defined
relation to tonal center – called
“tonal function”
Musical Tonality, con’t
Major tonality
Tonality of C Major
Level 1:
Level 2:
Level 3:
Level 4:
E
D
3rd and 5th scale degrees
G
F A B
C# D# F# G# A#
Diatonic Scale:
Semitones:
Tonic, 1st scale degree
C
Diatonic scale degrees
Non-diatonic scale tones
C D E F G A B C
2
2 1 2
2
2
1
Musical Tonality, con’t
Minor tonality
Tonality of C Minor (Harmonic)
Level 1:
Level 2:
Level 3:
Level 4:
Tonic, 1st scale degree
C
Eb
D
3rd and 5th scale degrees
G
F Ab
B
Diatonic scale degrees
C# E F# A A#
Diatonic Scale:
Semitones:
C Minor (Natural)
C Minor (Melodic)
Non-diatonic scale tones
C D Eb F G Ab B C
2
1
2
2
1
3
1
Musical Tonality, con’t
•
Additional points about tonality
• Can be transposed to begin on ANY of
the 12 chromatic pitches
• Thus, there are 12 major and 12
minor tonalities
• 24 tonalities in all
• Tonalities vary in terms of how related
they are to one another
• Relation between tonalities can be
assessed in terms of overlap
between notes of “diatonic set”
Diatonic Sets
Scale #
Major
C major
G major
D major
0
C
G
D
1
2
3
D
A
E
4
5
6
7
E F
B C
F# G
G
D
A
8
Natural minor
C minor
C
A minor
A
E minor
E
D Eb
B C
F# G
F
D
A
G
E
B
Ab
F
C
Harmonic minor
C minor
C
D
F
G
Ab
Eb
9
10 11
A
E
B
B
F#
C#
Bb
G
D
B
Diatonic Set Overlaps
C C# D
C Major
Major
G major
F major
A major
F# major
C
C
C
D# E F F# G G# A A# B Overlap
D
E F
D
D
C# D
C# D#
G
A
B
E
F# G
A
B
E F
G
A Bb
E
F#
G# A
B
F F#
G#
A# B
6
6
4
2
Natural minor
C minor C
A minor C
G minor C
D
D
D
Eb
F
E F
Eb
F
G Ab
Bb
G
A
B
G
A Bb
4
7
5
Harmonic minor
C minor C
D
Eb
G Ab
5
F
B
Diatonic Set Overlaps, con’t
The Circle of Fifths
Significance of Tonal
Structure
•
What is the psychological significant of
tonal structure?
• Psychological principle that certain
perceptual and conceptual objects have
special psychological status
• Classic work by Rosch (1975)
• Certain members in a group are
normative, best example of category
• Cognitive reference points for
judging members of category
• Exs, vertical and horizontal lines,
numbers that are multiples of 10,
focal colors
• Evidence for this structure?
• Ratings of goodness or typicality
• Memory for exemplars
• Description of hierarchical ordering
seems applicable to tonality
The Probe Tone Method
Krumhansl & Shepard (1979)
Context:
Probe Tone(s):
Task:
Rate how well the probe tone fit with
the previous passage in a musical
sense.
The Tonal Hierarchy
Krumhansl & Shepard (1979)
The Tonal Hierarchy, con’t
Major and Minor Key Profiles
(Krumhansl & Kessler, 1982)
The Tonal Hierarchy, con’t
C and F# Major Key Profiles
Perceiving Bitonality
The Petroushka Chord
(Krumhansl & Schmuckler, 1986)
Perceiving Bitonality, con’t
The Petroushka Chord
(Krumhansl & Schmuckler, 1986)
C Major
Ratings
F# Major
Ratings
Perceiving Bitonality, con’t
The Petroushka Chord
(Krumhansl & Schmuckler, 1986)
Bitonal
Ratings
Perceiving Atonality
Serial Music
(Krumhansl, Sandell, & Sargent,1987)
Tone Rows for Schoenberg’s Wind
Quintet (1924) and String Quartet
no. 4 (1936).
Perceiving Atonality, con’t
Serial Music
(Krumhansl, Sandell, & Sargent,1987)
Probe Tone Ratings
Group 1
Group 2
Perceiving Non-Western
Tonality
Classical Indian Music
(Castellano, Bharucha, & Krumhansl,1984)
Perceiving Non-Western
Tonality, con’t
Classical Indian Music
(Castellano, Bharucha, & Krumhansl,1984)