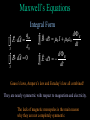* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Lecture32
National Electrical Code wikipedia , lookup
Residual-current device wikipedia , lookup
Electrical resistance and conductance wikipedia , lookup
Electrostatics wikipedia , lookup
Magnetic field wikipedia , lookup
Wireless power transfer wikipedia , lookup
Alternating current wikipedia , lookup
Force between magnets wikipedia , lookup
Superconducting magnet wikipedia , lookup
Hall effect wikipedia , lookup
Magnetoreception wikipedia , lookup
Induction heater wikipedia , lookup
Multiferroics wikipedia , lookup
Magnetochemistry wikipedia , lookup
Magnetic core wikipedia , lookup
Magnetic monopole wikipedia , lookup
Galvanometer wikipedia , lookup
Superconductivity wikipedia , lookup
Electrical injury wikipedia , lookup
Electric machine wikipedia , lookup
Electric current wikipedia , lookup
History of electromagnetic theory wikipedia , lookup
History of electrochemistry wikipedia , lookup
Eddy current wikipedia , lookup
Magnetohydrodynamics wikipedia , lookup
Scanning SQUID microscope wikipedia , lookup
Electricity wikipedia , lookup
Electromotive force wikipedia , lookup
Computational electromagnetics wikipedia , lookup
Maxwell's equations wikipedia , lookup
Electromagnetic field wikipedia , lookup
Lorentz force wikipedia , lookup
Mathematical descriptions of the electromagnetic field wikipedia , lookup
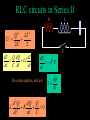
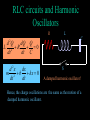
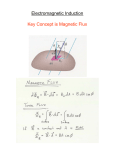
Announcements Change of plans for today: Demos on light and selected review for today Faraday’s Law 10 5T 10 m What is the current induced in this circuit? A) 30A B) 3A C) 10A D) 6A 3 m/s 2m Faraday’s Law 10 5T 10 m As the bar moves a current is induced! 3 m/s 2m dB E dt There are no batteries anywhere, so we say that a current is induced, by an induced emf. Hence, an electric current can be induced in a circuit by a changing magnetic field, in the opposite direction to the change in flux. Comparision of Induction dE B ds 0 I 0 0 dt dB E ds dt •No magnetic monopole, hence no magnetic current •Electric fields and magnetic fields induce in opposite fashions Faraday’s Law and Electric Fields dB E ds dt . A cylindrical region of radius R = 3.0 cm contains a uniform magnetic field parallel to its axis. The field is 0 outside the cylinder. If the field is changing at the rate 0.60 T/s, the electric field induced at a point 2R from the cylinder axis is: Using Faraday’s law: 2p (2R)E =-p(R2) dB/dt, so E= (-(R2) /4) dB/dt=0.0045 V/m Maxwell’s Equations Integral Form qin E dA S B dA 0 S 0 dE B ds 0 I 0 0 dt dB E ds dt Gauss’s laws, Ampere’s law and Faraday’s law all combined! They are nearly symmetric with respect to magnetism and electricity. The lack of magnetic monopoles is the main reason why they are not completely symmetric. Quiz The Thediagrams diagramsshow showthree threecircuits circuitswith withidentical identicalbatteries, batteries,identical identicalinductors, inductors, and after the switch isisclosed which the andidentical identicalresistors. resistors.Just A Just very after long the time switch later, which closedhas which thehas has least theleast greatest current currentthrough throughthe thebattery? battery? RL - Circuits I •What happens when the switch S is closed at t = 0? •Let I be the current in the circuit R E + L – •Use Kirchoffs rule for loops on the circuit dI E R dI I 0 E RI L dt L L dt E E Rt / L t / I t ) 1 e 1 e ) ) R R L/ R S RC–Circuits vs RL-Circuits t RC I e R •At t=0, ordinary wire •As t-> infinity, broken wire tR I 1 e L R •At t=0, broken wire, little current for small t •As t-> infinity, ordinary wire •In terms of current control, an inductor can often be considered as the opposite of a capacitor LC – Circuits and Energy + V E cos t ) – I CE sin t ) C L S1 1/ LC S2 At an arbitrary time t, where is the energy stored in this circuit? A) In the capacitor B) In the inductor C) Alternately in the capacitor or the inductor D) What energy? U C C V ) CE cos t ) 2 1 2 1 2 2 2 U tot C E 1 2 2 U L LI 12 LC 2E 2 2 sin 2 t ) 12 CE 2 sin 2 t ) 1 2 2 E I C – •Switch S1 is closed, then opened. •At t = 0, switch S2 is closed. •What happens? + LC - Circuits L S1 S2 V t 0) E dQ I Q C V dt 2 2 d V ) d Q dI V L L 2 CL dt dt dt 2 LC – Circuits and Harmonic Oscillators V CL d 2 V ) dt 2 V E cos t ) m d 2x x 2 k dt x A cos(t ) There are many correspondances between These equations electrical and mechanical systems! RLC circuits in Series II R L Q 2 LI 2 U 2C 2 S dU Q dQ dI LI dt C dt dt dU I 2R dt Do some algebra, and use 2 d Q dQ Q L 2 R 0 dt dt C dQ I dt C RLC circuits and Harmonic Oscillators R L C 2 d Q dQ Q L 2 R 0 dt dt C 2 d x dx m 2 b kx 0 dt dt S A damped harmonic oscillator! Hence, the charge oscillations are the same asdU the motion 2 of a I R damped harmonic oscillator. dt Quiz A. B. C. D. Electromagnetic Waves ck kE0 B0 Ey E0 cos kx t ) E0 cB0 E y cBz Bz B0 cos kx t ) Electric Magnetic Field Field Direction of Motion Using Maxwell’s Equations E y Ex Bz x y t By By Ex Ez z x t E y Bx Bz 0 0 z x t Bx Ez E y y z t Ex Bz By 0 0 y z t Bx Ez 0 0 x y t Electromagnetic Waves E y Bz x t E y Bz 0 0 x t •These equations look like sin functions will solve them. Ey E0 cos kx t ) Bz B0 cos kx t ) kE0 sin kx t ) B0 sin kx t ) kB0 sin kx t ) 0 0 E0 sin kx t ) kE0 B0 kB0 0 0 E0 Electromagnetic Waves kE0 B0 kB0 0 0 E0 •These equations imply k E0 B0 0 0 B0 E0 2 2 k 1 0 0 2 k 2 1 0 0 c 2.998 108 m/s •The speed of light (in vacuum)