Download Ch. 32 Electromagnetic Waves

Electromagnetic Waves Ch. 32
Maxwell’s equations
Plane EM waves & speed of light
The EM spectrum
C 2012 J. F. Becker
(sec. 32.1)
(sec. 32.2)
(sec. 32.6)
Learning Goals - we will learn: ch 32
• Maxwell’s Equations – the four fundamental
equations of EM theory.
• How the speed of light is related to the
fundamental constants of electricity and
magnetism (eo and mo).
• How to describe propagating and standing
EM waves.
MAXWELL’S EQUATIONS
The relationships between electric
and magnetic fields and their
sources can be stated compactly in
four equations, called
Maxwell’s equations.
Together they form a complete
basis for the relation of E and B
fields to their sources.
C 2004 Pearson Educational / Addison Wesley
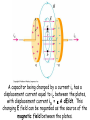
A capacitor being charged by a current ic has a
displacement current equal to iC between the plates,
with displacement current iD = e A dE/dt. This
changing E field can be regarded as the source of the
magnetic field between the plates.
A capacitor being charged by a current iC has a
displacement current equal to iC in magnitude between
the plates, with
DISPLACEMENT CURRENT iD = e A dE/dt
From C = e A / d and DV = E d we can use
q = C V to get
q = (e A / d ) (E d ) = e E A = e F E and
from iC = dq / dt = e A dE / dt = e dF E / dt = iD
We have now seen that
a changing E field can produce a B field
and from Faraday’s Law
a changing B field can produce an E field (or emf)
C 2012 J. Becker
MAXWELL’S EQUATIONS
The relationships between electric
and magnetic fields and their
sources can be stated compactly in
four equations, called
Maxwell’s equations.
Together they form a complete
basis for the relation of E and B
fields to their sources.
C 2004 Pearson Educational / Addison Wesley
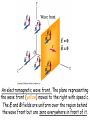
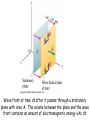
An electromagnetic wave front. The plane representing
the wave front (yellow) moves to the right with speed c.
The E and B fields are uniform over the region behind
the wave front but are zero everywhere in front of it.
Gaussian surface for an electromagnetic
wave propagating through empty space.
The total electric flux and
total magnetic flux through
the surface are both zero.
Both E and B are _ to
the direction of
propagation.
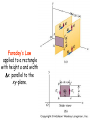
Applying Faraday’s Law to a plane wave.
E dl = -d/dt{FB }= - d/dt B dA
LH:  E o dl = -Ea
RH: In time dt the wave front
moves to the right a distance c dt.
The magnetic flux through the
rectangle in the xy-plane
increases by an amount d FB equal
to the flux through the shaded
rectangle in the xy-plane with
area ac dt, that is,
d FB =B ac dt; d FB /dt = B ac
-d FB / dt = -B ac
and (LH = RH):
-Ea = -B ac. So
E = Bc
Applying Ampere’s Law to a plane wave: iC = 0
B
dl = mo iC + mo eo d FE /dt
LH:  B o dl = Ba
RH: In time dt the wave front
moves to the right a distance
c dt. The electric flux through
the rectangle in the xz-plane
increases by an amount dFE equal
to E times the area ac dt of the
shaded rectangle, that is,
d FE = E ac dt. Thus
d FE / dt = E ac, and (LH = RH):
Ba = mo eo Eac  B = mo eo Ec
and from E = Bc and B = mo eo Ec
we must have c = 1 / (mo eo
1/2
)
= 3.00
8
(10)
m/sec
Faraday’s Law
applied to a rectangle
with height a and width
Dx parallel to the
xy-plane.
Ampere’s Law
applied to a rectangle
with height a and width
Dx parallel to the
xz-plane.
WAVE PROPAGATION
SPEED
c = 1 / (mo eo)1/2
c = 3.00 (10)8 m/sec
Representation of the electric and magnetic fields in a
propagating wave. One wavelength is shown at
time t = 0. Propagation direction is E x B.
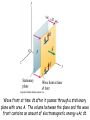
Wave front at time dt after it passes through a stationary
plane with area A. The volume between the plane and the wave
front contains an amount of electromagnetic energy uAc dt.
ENERGY AND MONENTUM IN EM WAVES
Energy density: u = eoE2 /2 + B2 /2 mo (Ch 30)
Using B = E/c = E (mo eo
u = eo
2
E
u = eo
u = eo
2
E
2
E
/2 +
1/2
)
2
E (mo eo)
/2 + eo
2
E /2
we get
/2 mo
= eo
2
E
(half in E and half in B)
(eqn 32.25)
ENERGY FLOW IN EM WAVES
dU = u dV = eo
2
E (Ac
dt)
Define the “Poynting” vector
S = energy flow / time x area
S = dU / dt A = eoE2 (Ac) / A = eo c E2
or
2
2
1/2
1/2
2
S = eo c E = eo E / (mo eo) = ( eo /mo ) E = EB / mo
And define the “Poynting” vector:
S = E x B / mo
With units of Joule/sec meter2 or Watt/meter2
Wave front at time dt after it passes through a stationary
plane with area A. The volume between the plane and the wave
front contains an amount of electromagnetic energy uAc dt.
A standing electromagnetic wave does not propagate
along the x-axis; instead, at every point on the x-axis
the E and B fields simply oscillate.
Examples of standing electromagnetic waves
Microwave ovens have a standing wave with l =
12.2 cm, a wavelength that is strongly absorbed
by water in foods. Because the wave has nodes
(zeros) every 6.1 cm the food must be rotated
with cooking to avoid cold spots!
Lasers are made of cavities of length L with
highly reflecting mirrors at each end to reflect
waves with wavelengths that satisfy L = m l / 2,
where m = 1, 2, 3, …
C 2012 J. Becker
THE ELECTROMAGNETIC SPECTRUM
The frequencies and wavelengths found in nature extend over
a wide range. The visible wavelengths extend from
approximately 400 nm (blue) to 700 nm (red).
One cycle in the production of an electro-magnetic wave
by an oscillating electric dipole antenna. The red
arrows represent the E field. (B not shown.)
PREPARATION FOR FINAL EXAM
At a minimum the following should be reviewed:
Gauss's Law - calculation of the magnitude of the electric field caused by
continuous distributions of charge starting with Gauss's Law and completing all the
steps including evaluation of the integrals.
Ampere's Law - calculation of the magnitude of the magnetic field caused by
electric currents using Ampere's Law (all steps including evaluation of the integrals).
Faraday's Law and Lenz's Law - calculation of induced voltage and current,
including the direction of the induced current.
Calculation of integrals to obtain values of electric field, electric potential, and
magnetic field caused by continuous distributions of electric charge and current
configurations (includes the Law of Biot and Savart for magnetic fields).
Maxwell's equations - Maxwell's contribution and significance.
DC circuits - Ohm's Law, Kirchhoff's Rules, series-parallel R’s, RC ckts, power.
Series RLC circuits - phasors, phase angle, current, power factor, average power.
Vectors - as used throughout the entire course.
Review
See
www.physics.sjsu.edu/becker/physics51
C 2012 J. F. Becker