* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Topic 5 - The Uncertainty Principle
Renormalization group wikipedia , lookup
Quantum tunnelling wikipedia , lookup
Quantum state wikipedia , lookup
ALICE experiment wikipedia , lookup
Identical particles wikipedia , lookup
Monte Carlo methods for electron transport wikipedia , lookup
Quantum vacuum thruster wikipedia , lookup
Matrix mechanics wikipedia , lookup
Renormalization wikipedia , lookup
Elementary particle wikipedia , lookup
Old quantum theory wikipedia , lookup
Symmetry in quantum mechanics wikipedia , lookup
ATLAS experiment wikipedia , lookup
EPR paradox wikipedia , lookup
Powder diffraction wikipedia , lookup
Compact Muon Solenoid wikipedia , lookup
Coherent states wikipedia , lookup
Angular momentum operator wikipedia , lookup
Relativistic quantum mechanics wikipedia , lookup
Relational approach to quantum physics wikipedia , lookup
Electron scattering wikipedia , lookup
Introduction to quantum mechanics wikipedia , lookup
Wave packet wikipedia , lookup
Photon polarization wikipedia , lookup
Bohr–Einstein debates wikipedia , lookup
Double-slit experiment wikipedia , lookup
Theoretical and experimental justification for the Schrödinger equation wikipedia , lookup
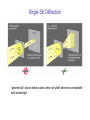
PHY 102: Quantum Physics Topic 5 The Uncertainty Principle The Uncertainty Principle •One of the fundamental consequences of quantum mechanics is that it is IMPOSSIBLE to SIMULTANEOUSLY determine the POSITION and MOMENTUM of a particle with COMPLETE PRECISION •Can be illustrated by a couple of “thought experiments”, for example the “photon picture” of single slit diffraction and the “Heisenberg Microscope” Single Slit Diffraction “geometrical” picture breaks down when slit width becomes comparable with wavelength Position of dark fringes in single-slit diffraction m sin a If, like the 2-slit treatment we assume small angles, sin ≈ tan =ymin/R, then ymin Rm a Positions of intensity MINIMA of diffraction pattern on screen, measured from central position. Very similar to expression derived for 2-slit experiment: n ym R d But remember, in this case ym are positions of MAXIMA In interference pattern Width of central maximum •We can define the width of the central maximum to be the distance between the m = +1 minimum and the m=-1 minimum: R R 2 R y a a a Intensity distribution image of diffraction pattern Ie, the narrower the slit, the more the diffraction pattern “spreads out” Single Slit Diffraction: Photon Picture Since θ is small: sin a a P Photons directed towards outer part of central maximum have momentum Py Px p px py py px px a px h h px a a ie, localizing photons in the y-direction to a slit of width a leads to a spread of y-momenta of at least h/a. Intensity distribution • So, the more we seek to localize a photon (ie define its position) by shrinking the slit width, a, the more spread (uncertainty) we induce in its momentum: • In this case, we have pyy ~ h Heisenberg Microscope Suppose we have a particle, whose momentum is, initially, precisely known. For convenience assume initial p = 0. “microscope” From wave optics (Rayleigh Criterion) sin D D From our diagram: y 2 x x sin y 2 2y 2 y x D Δx Heisenberg Microscope 2 y x D Since this is a “thought experiment” we are free from any practical constraints, and we can locate the particle as precisely as we like by using radiation of shorter and shorter wavelengths. “microscope” D y 2 But what are the consequences of this? Δx Heisenberg Microscope In order to see the particle, a photon must scatter off it and enter the microscope. Thus process MUST involve some transfer of momentum to the particle……. “microscope” BUT there is an intrinsic uncertainty in the Xcomponent of the momentum of the scattered photon, since we only know that the photon enters the microscope somewhere within a cone of half angle : Δp =2psin p p By conservation of momentum, there must be the same uncertainty in the momentum of the observed particle…………… Heisenberg Microscope: Summary Uncertainty in position of particle: 2 y x D Can reduce as much as we like by making λ small…… Uncertainty in momentum of particle: 2h D p 2 p photon sin 2y So, if we attempt to reduce uncertainty in position by decreasing λ, we INCREASE the uncertainty in the momentum of the particle!!!!!! Product of the uncertainties in position and momentum given by: 2 y Dh xp 2h D y The Uncertainty Principle Our microscope thought experiments give us a rough estimate for the uncertainties in position and momentum: xp ~ h “Formal” statement of the Heisenberg uncertainty principle: x p 2 The Uncertainty Principle: wave picture Consider a particle of known kinetic energy moving freely through space. Wave function: ( x, t ) A sin( kx t ) Momentum is exactly defined, but position of particle completely undefined...................... What happens if we combine waves of different wavelength? Beats (from sound waves) These occur from the superposition of 2 waves of close, but different frequency: f beat f a f b f Δt ft 1 Δt •So, by combining waves of different wavelength, we can produce localized “wave groups” •The more different wavelengths we combine, the greater the degree of localization of the wave group (ie particle postition becomes more well-defined) •We can obtain a totally localized wavefunction (x =0) only by combining an infinite number of waves with different wavelength •We thus lose all knowledge of the momentum of the particle... Energy-time Uncertainty •Uncertainty principle also applies to simultaneous measurements of energy and time Et h Stationary state Zero energy spread Decay to lower state with finite lifetime t: Energy broadening E (explains, for example “natural linewidth” In atomic spectra)