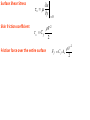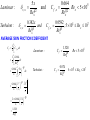* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download File
Thermal comfort wikipedia , lookup
Insulated glazing wikipedia , lookup
Solar water heating wikipedia , lookup
Radiator (engine cooling) wikipedia , lookup
Building insulation materials wikipedia , lookup
Thermoregulation wikipedia , lookup
Heat equation wikipedia , lookup
Intercooler wikipedia , lookup
Thermal conductivity wikipedia , lookup
Underfloor heating wikipedia , lookup
Heat exchanger wikipedia , lookup
Solar air conditioning wikipedia , lookup
Dynamic insulation wikipedia , lookup
Copper in heat exchangers wikipedia , lookup
Hyperthermia wikipedia , lookup
Cutting fluid wikipedia , lookup
R-value (insulation) wikipedia , lookup
Reynolds number wikipedia , lookup
Convection Prepared by: Nimesh Gajjar CONVECTIVE HEAT TRANSFER 20°C 5 m/s AIR . Q 20°C a) Forced Convection AIR . Q Warmer air rising b) Free Convection No convection current AIR c) Conduction Convection heat transfer involves • fluid motion • heat conduction The fluid motion enhances the heat transfer, since it brings hotter and cooler chunks of fluid into contact, initiating higher rates of conduction at a greater number of sites in fluid. Therefore, the rate of heat transfer through a fluid is much higher by convection than it is by conduction. In fact, the higher the fluid velocity, the higher the rate of heat transfer. Convection heat transfer strongly depends on • fluid properties dynamic viscosity , thermal conductivity k, density and specific heat • fluid velocity V • Geometry and the roughness of the solid surface • Type of fluid flow (such as being laminar or turbulent). NEWTON’S LAW OF COOLING Qconv hAs Ts T h = Convection heat transfer coefficient As = Heat transfer surface area Ts = Temperature of the surface T= Temperature of the fluid sufficiently far from the surface LOCAL HEAT FLUX qconv hl Ts T qconv hl is the local convection coefficient TOTAL HEAT TRANSFER RATE Qconv Qconv q conv As Qconv Ts T dAs 1 h As h dA l s As hl dAs As Local and total convection transfer (a) Surface of arbitrary shape. (b) Flat plate. q” V ,T U ,T dAs q” As, Ts As, Ts x dx L A fluid flowing over a stationary surface comes to a complete stop at the surface because of the no-slip condition. Uniform approach velocity, V Relative velocity of fluid layers Zero velocity at the surface Solid Block A similar phenomenon occurs for the temperature. When two bodies at different temperatures are brought into contact, heat transfer occurs until both bodies assume the same temperature at the point of contact. Therefore, a fluid and a solid surface will have the same temperature at the point of contact. This is known as NO-TEMPERATURE-JUMP CONDITION. An implication of the no-slip and the no-temperature jump conditions is that heat transfer from the solid surface to the fluid layer adjacent to the surface is by pure conduction, since the fluid layer is motionless, qconv qcond k fluid T dy y 0 T represents the temperature distribution in the fluid T y y 0 is the temperature gradient at the surface. hl Ts T qconv h k fluid T y y 0 Ts T NUSSELT NUMBER hLc Nu k k is the thermal conductivity of the fluid Lc is the characteristic length Heat transfer through a fluid layer of thickness L and temperature difference T2 Heat transfer through the fluid layer will be by convection when the fluid involves some motion and by conduction when the fluid layer is motionless. . Fluid layer qconv hT Q T1 ΔT = T2 – T1 qcond k T L qconv hL hT Nu qcond k T L k Nusselt number - enhancement of heat transfer through a fluid layer as a result of convection relative to conduction across the same fluid layer. Larger the Nusselt number, the more effective the convection. Nu = 1 for a fluid layer - heat transfer across the layer by pure conduction Internal and external flows EXTERNAL FLOW - The flow of an unbounded fluid over a surface such as a plate, a wire, or a pipe INTERNAL FLOW - flow in a pipe or duct, if the fluid is completely bounded by solid surfaces External flow Air Internal flow Water Laminar versus Turbulent Flow Some flows are smooth and orderly while others are rather chaotic. The highly ordered fluid motion characterized by smooth streamlines is called laminar. The flow of high-viscosity fluids such as oils at low velocities is typically laminar. The highly disordered fluid motion that typically occurs at high velocities characterized by velocities fluctuations is called turbulent. The flow of low-viscosity fluids such as air at high velocities is typically turbulent. The flow regime greatly influences the heat transfer rates and the required power for pumping Laminar Dye Pipe Transitional Q = VA Dye Streak Turbulent Smooth well rounded Entrance Osborne Reynolds in 1880’s, discovered that the flow regime depends mainly on the ratio of the inertia forces to viscous forces in the fluid. The Reynolds number can be viewed as the ratio of the inertia forces to viscous forces acting on a fluid volume element. Inertia forces VLc VLc Re Viscous One, Two and Three Dimensional Flows V(x, y, z) in cartesian or V(r, , z) in cylindrical coordinates velocity profile (remains unchanged) V(r) r z One-dimensional flow in a circular pipe VELOCITY BOUNDARY LAYER Laminar boundary-layer V Transition Turbulent boundary-layer region U U Turbulent layer y Buffer layer Laminar layer x xcr V Boundary-layer thickness, δ Relative velocity of fluid layers U V INVISCID FLOW REGION 0.99V δ Zero velocity at the surface (No slip condition) BOUNDARY LAYER REGION Development of a boundary layer on a surface is due to the no-slip condition Surface Shear Stress Skin friction coefficient u s y s Cf y 0 V 2 Friction force over the entire surface 2 Ff C f As V 2 2 THERMAL BOUNDARY LAYER Free Stream T Uniform Temperature T t Ts Thermal boundary layer Ts 0.99 (T Ts ) Thermal boundary layer on a flat plate (the fluid is hotter than the plate surface) The thickness of the thermal boundary layer, at any location along the surface is define as the distance from the surface at which the temperature difference T – Ts equals 0.99(T– Ts). For the special case of Ts = 0, we have T = 0.99 at the outer edge of the thermal boundary layer, which is analogous to u = 0.99 for the velocity boundary layer. Shape of the temperature profile in the thermal boundary layer dictates the convection heat transfer between a solid surface and the fluid flowing over it. In flow over a heated (or cooled) surface, both velocity and thermal boundary layers will develop simultaneously. Noting that the fluid velocity will have a strong influence on the temperature profile, the development of the velocity boundary layer relative to the thermal boundary layer will have a strong effect on the convection heat transfer. PRANDTL NUMBER The relative thickness of the velocity and the thermal boundary layers is described by the dimensionless parameter Prandtl number, defined as Molecular diffusivity of momentum C p Pr Molecular diffusivity of heat k TYPICAL RANGES OF PRANDTL NUMBERS FOR COMMON FLUIDS Fluid Pr Liquid metals 0.004-0.030 Gases 0.7-1.0 Water 1.7-13.7 Light organic fluids 5-50 Oils 50-100,000 Glycerin 2000-100,000 v,x La min ar : v,x Turbulent : 5x Re1x 2 0.382 x C f ,x and and C f ,x Re1x 5 AVERAGE SKIN FRICTION COEFFICIENT 0.664 Re1x 2 0.0592 Re1x 5 , Rex 5 105 , 5 105 Rex 107 L 1 C f C f ,x dx L0 La min ar : Cf L 1 0.664 dx L 0 Re1x 2 L 0.664 Vx L 0 0.664 V L 1 2 1 2 Turbulent : dx L x1 2 2 0.664 VL L 1.328 12 ReL 1 2 1 2 0 Cf 1.328 Re1L 2 0.074 Re1L 5 Re 5 105 5 105 ReL 107 Problem: Engine oil at 60° C flows over the upper surface of a 5-m long flat plate whose temperature is 20° C with a velocity of 2 m/s (Fig 2.12). Determine the total drag force and the rate of heat transfer per unit width of the entire plate. T 60 C V2m s Oil Ts 20 C A L= 5 m Known: Engine oil flows over a flat plate. Find: The total drag force and the rate of heat transfer per unit width of the plate are to be determined. Assumptions: The flow is steady and incompressible. The critical Reynolds number is . Recr 5 105 T f Ts T 2 20 60 2 40o C 876 kg m3 Pr 2870 k 0.144 W m C 242 106 m 2 s ReL VL 2 m s 5 m 242 10-6 m 2 s C f 1.328 ReL0.5 1.328 41322 FD C f As Nu V 2 2 6.533 103 5 1m2 which is less than the critical Reynolds number 41322 0.5 6.533103 876 kg m 2 m s 3 2 2 1N = 57.23 N 2 1kg m s hL 0.5 0.664 ReL0.5 Pr1 3 0.664 41322 28701 3 1918 k 0.144 W m C k 2 o h Nu = 1918 55.2 W m C L 5m Q hAs T Ts 55.2 W m2 C 5 1m2 60 20 C =11, 049 W o o Note that, heat transfer is always from the higher-temperature medium to the lowertemperature one. In this case, it is from the oil to the plate. The heat transfer rate is per m width of the plate. The heat transfer for the entire plate can be obtained by multiplying the value obtained by the actual width of the plate. Problem: A long 10-cm diameter steam pipe whose external surface temperature is 110oC passes through some open area that is not protected against the winds (Fig. 2.23). Determine the rate of heat loss from the pipe per unit length of its length when the air is at 1 atm pressure and 10oC and the wind is blowing across the pipe at a velocity of 8 m/s. Schematic: Wind Known: A steam pipe is exposed to windy air. Find: The rate of heat loss from the steam is to be determined. Ts = 110o C Assumptions: •Steady operating conditions exist. •Radiation effects are negligible. •Air is an ideal gas. The properties of air at the average film temperature of T f Ts T 2 k 0.02808 W m C = (110 + 10)/2 =60 Pr = 0.7202 = 1.896 10-5 m2 s Re Nu VD 8m s 0.1m 4.219 104 1.896 105 m2 s 12 13 0.62 Re Pr hD 0.3 14 k 1 0.4 Pr 2 3 0.3 0.62 4.219 104 = 124.44 12 Re 5 8 1 282 , 000 0.7202 1 3 1 0.4 0.7202 2 3 1 4 45 45 4 5 8 1 4.219 10 282,000 h k 0.02808 W m C Nu = 124.44 34.94 W m 2 C D 0.1m As pL DL 0.1m 1m 0.314 m 2 Q hAs Ts T 34.94 W m 2 C 0.314 m 2 110 10 C = 1097.3 W Important numbers Nusselt number Reynolds number Prandtl number Grashof number Biot number hL Nu k Re L Pr Gr Convection Conduction UoL Inertial force Viscous force Momentum diffusivity a Thermal diffusivity g Ts T L3 hL Bi k solid 2 Buoyancy forces Viscous forces thermal internal resistance surface film resistance Reference book: Fundamentals of Heat and Mass Transfer, Incropera & DeWitt