Download Ch 29

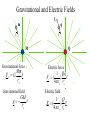
The Electric Field
• The concept of electric fields was invented by
Michael Faraday to describe his model of how
charges interact.
• Charges interact by exerting forces on each
other. Faraday considered the forces as “lines of
force” (sort of like strings) with density in space
proportional to the strength of the force.
The Electric Field (cont’d)
•However, the force between two charges is
dependent on the value of both charges.
•Therefore, consider the force at a point in space
that a charge would exert on a positive test charge
with one unit of charge (1 C). It is the force per
unit charge exerted by the first charge.
•THIS IS THE ELECTRIC FIELD ASSOCIATED
WITH THE CHARGE IN QUESTION!!!! -
The Electric Field
• It is the spatial
distribution of force
per unit charge
• Mathematically we
define it as
E
F
q
test
E
q
Gravitational and Electric Fields
Fe
m
r
q
r
M
Gravitational force
Mm
F G
rˆ
r
G
2
12
Gravitational field
GM
g
rˆ
r
2
12
Q
Electric force
1 Qq
Fe  (
) 2 rˆ
4 0 r12
Electric field
1
Q
E (
) rˆ
4 r
2
0
12
Properties of Electric Field
• Magnitude of E defined as kQ/r2.
• Direction defined by lines of force, field
lines. Force felt by a positve test charge.
• Density of lines of force proportional to
magnitude of E.
• Superposition Law holds. E is a vector.
The Electric Dipole

+q
E = E+ + E-
r
q
1
E

E

(
)
x
  4 ( x2  d 2 )
d
E+
0
4
EE  E cos  E cos  2E cos
-q
E
d
2
cos 
1
( x2  d 2 ) 2
4
qd
E  ( 1 )
4
3
2
0 ( x2  d ) 2
Electric dipole moment
4
p = qd
When d<<x
E ( 1 ) p
4 x3
0
Electric fields from a distribution of charge
Up to now we have only described the electric field of point
charges.
Clearly we make surfaces of charge and determine the
resulting electric field distribution.
density of field lines proportional to
electric field strength
Electric Field from some Continuous
Charge Distributions
(Hint: always take advantage of symmetry)
• Ring of charge
1
qz
1
q
E (
)
(
)
4 (z  R )
4 z
z
2
2
3
2
2
0
0
z
Thin ring with
charge q
R
Electric Field from Some Continuous
Charge Distributions
• Ring of charge
1
qz
1
q
E (
)
(
)
4 (z  R )
4 z
z
2
2
3
2
2
0
0
• Disc of charge

z

E 
(1 
)
2
z R
2
z
2
0
when z
gets big
2
0
when R
gets big
the disc is an
infinite plane
(Obtain the disc by treating it as made up of thin rings.
Use the thin rings as elements of charge and integrate.)
Electric Field from some Continuous
Charge Distributions
• Ring of charge
1
qz
1
q
E (
)
(
)
4 (z  R )
4 z
z
2
2
3
2
2
0
0
• Disc of charge

z

E 
(1 
)
2
z R
2
z
2
2
0
• Infinite line of charge


E

2 y
2 r
0
0
0
Try to find the electric field
of an infinite plane using the
infinite line as an elemental charge.
Charges in Electric Fields
qE
+ + + + + + +
Point charges in Electric fields
-q
Force F = qE
E
- - - - - - mg
Dipoles in Electric fields
+q
d
Torque= p x E
Potential energy
F+
E
F-
U=-p.E

p
-q
p

(into page)
E
Homework No. 1
Chapter 23
Problems: 3, 9, 28, 44
Reading Assignment:
Review the Chapter 23 Synopsis p 577-578
Study Chapter 24 p 585 - 592