Download Class 15- Sections: 7.3

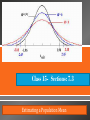
Class
 15-Sections: 7.3
Estimating a Population Mean
This section presents methods for using the sample mean to
make an inference about the value of the corresponding
population mean.
1. We should know that the sample mean is the best
point estimate of the population mean μ.
2. We should learn how to use sample data to construct
a confidence interval for estimating the value of a
population mean, and we should know how to
interpret such confidence intervals.
3. We should develop the ability to determine the sample
size necessary to estimate a population mean.




Best point estimate for  is the sample mean
x
Usually when trying to estimate ,  is unknown,
and only in rare cases will  be known.
Just because x is the best point estimate, we still
need to know how good that estimate is.
So we need to construct a confidence interval
(interval estimate) which consist a range of values
to estimate , instead of a single value.
In order to construct CI for the mean we will
have to go by cases:
I. Is the population normally distributed?
II. Is the sample size greater or less than 30?
III. Is the population standard deviation
known?
Population is normally distributed
or sample size > 30
and the population standard
deviation
 is known.
x
In this case we use the z-score to estimate
the population mean and create the CI.
Where
E  z 2

n
The procedure we used has a requirement that
the population is normally distributed or the
sample size is greater than 30.
In this case  is known
What if  is unknown?
In this case we cannot use the Standard
Normal distribution
Instead we will be using the student
t-distribution
If a population has a normal distribution, then the
distribution of
is a Student t Distribution for all samples of size n.
It is often referred to as a t distribution and is used to
find critical values denoted by
.
Where
ta
has n -1 degrees of freedom
2
See table A-3 for the values of
ta
2

The number of degrees of freedom for a
collection of sample data is the number of
sample values that can vary after certain
restrictions have been imposed on all data
values.

The degree of freedom is often abbreviated df.
degrees of freedom = n – 1
for the methods in this section
μ
= population mean
= sample mean
s
= sample standard deviation
n
= number of sample values
E
= margin of error
t α/2
= critical t value separating an area of α/2 in
the right tail of the t distribution
Where
found in Table A-3
df = n-1
1. Verify that the requirements are satisfied.
2. Using n-1 degrees of freedom refer to Table A-3 to find
3. Evaluate the margin of error
4. Find the values of x  E and x  E. Substitute those values
in the general format for the CI.
x E    x E
5. Round the resulting CI limits
In a test of weight loss programs, 40 adults used the
Atkins weight loss program. After 12 months, their
mean weight loss was found to be 2.1 lb, with a
standard deviation of 4.8lb. Construct a 90% CI
estimate of the mean weight loss of all such
subjects.
Does the Atkins program appear to be effective?
Does it appear to be practical?
1. The Student t distribution is different for different sample
sizes. (See the following slide for the cases n = 3 and n = 12.)
2. The Student t distribution has the same general symmetric
bell shape as the standard normal distribution but it reflects
the greater variability (with wider distributions) that is
expected with small samples.
3. The Student t distribution has a mean of t = 0 (just as the
standard normal distribution has a mean of z = 0).
4. The standard deviation of the Student t distribution varies
with the sample size and is greater than 1 (unlike the
standard normal distribution, which has σ = 1).
5. As the sample size n gets larger, the Student t distribution
gets closer to the normal distribution.
Point estimate of μ:
= (upper confidence limit) + (lower confidence limit)
2
Margin of Error:
E
= (upper confidence limit) – (lower confidence limit)
2
  populationmean
  populationstandard deviation
x samplemean
Edesired marginof error
za   zscorewithareaof a intherighttailof SND
2
2
 
 z 
 a2 
n
E 




2
Always round up to the
next larger whole number
Find the sample size required to estimate the mean
IQ of students currently taking a statistics course.
Assume that we want 99% confidence that the mean
from the sample is within two IQ points of the true
population mean.
Also assume that  = 15
1. Use the range rule of thumb to estimate the standard
deviation as follows:
2. Start the sample collection process without knowing σ
and, using the first several values, calculate the sample
standard deviation s and use it in place of σ. The
estimated value of σ can then be improved as more
sample data are obtained, and the sample size can be
refined accordingly.
3. Estimate the value of σ by using the results of some
other earlier study.



Use Normal (z) distr. :  is known and
normally distributed
population or n>30
Use t distribution:
 unknown and
normally distributed
population or n>30
Use nonparametric :
population is not
normally distributed
and n<30

http://www.matematicasvisuales.com/english/html/probab
ility/varaleat/tstudent.html