* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Class 15- Sections: 7.3
Survey
Document related concepts
Transcript
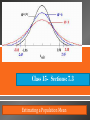
Class 15-Sections: 7.3 Estimating a Population Mean This section presents methods for using the sample mean to make an inference about the value of the corresponding population mean. 1. We should know that the sample mean is the best point estimate of the population mean μ. 2. We should learn how to use sample data to construct a confidence interval for estimating the value of a population mean, and we should know how to interpret such confidence intervals. 3. We should develop the ability to determine the sample size necessary to estimate a population mean. Best point estimate for is the sample mean x Usually when trying to estimate , is unknown, and only in rare cases will be known. Just because x is the best point estimate, we still need to know how good that estimate is. So we need to construct a confidence interval (interval estimate) which consist a range of values to estimate , instead of a single value. In order to construct CI for the mean we will have to go by cases: I. Is the population normally distributed? II. Is the sample size greater or less than 30? III. Is the population standard deviation known? Population is normally distributed or sample size > 30 and the population standard deviation is known. x In this case we use the z-score to estimate the population mean and create the CI. Where E z 2 n The procedure we used has a requirement that the population is normally distributed or the sample size is greater than 30. In this case is known What if is unknown? In this case we cannot use the Standard Normal distribution Instead we will be using the student t-distribution If a population has a normal distribution, then the distribution of is a Student t Distribution for all samples of size n. It is often referred to as a t distribution and is used to find critical values denoted by . Where ta has n -1 degrees of freedom 2 See table A-3 for the values of ta 2 The number of degrees of freedom for a collection of sample data is the number of sample values that can vary after certain restrictions have been imposed on all data values. The degree of freedom is often abbreviated df. degrees of freedom = n – 1 for the methods in this section μ = population mean = sample mean s = sample standard deviation n = number of sample values E = margin of error t α/2 = critical t value separating an area of α/2 in the right tail of the t distribution Where found in Table A-3 df = n-1 1. Verify that the requirements are satisfied. 2. Using n-1 degrees of freedom refer to Table A-3 to find 3. Evaluate the margin of error 4. Find the values of x E and x E. Substitute those values in the general format for the CI. x E x E 5. Round the resulting CI limits In a test of weight loss programs, 40 adults used the Atkins weight loss program. After 12 months, their mean weight loss was found to be 2.1 lb, with a standard deviation of 4.8lb. Construct a 90% CI estimate of the mean weight loss of all such subjects. Does the Atkins program appear to be effective? Does it appear to be practical? 1. The Student t distribution is different for different sample sizes. (See the following slide for the cases n = 3 and n = 12.) 2. The Student t distribution has the same general symmetric bell shape as the standard normal distribution but it reflects the greater variability (with wider distributions) that is expected with small samples. 3. The Student t distribution has a mean of t = 0 (just as the standard normal distribution has a mean of z = 0). 4. The standard deviation of the Student t distribution varies with the sample size and is greater than 1 (unlike the standard normal distribution, which has σ = 1). 5. As the sample size n gets larger, the Student t distribution gets closer to the normal distribution. Point estimate of μ: = (upper confidence limit) + (lower confidence limit) 2 Margin of Error: E = (upper confidence limit) – (lower confidence limit) 2 populationmean populationstandard deviation x samplemean Edesired marginof error za zscorewithareaof a intherighttailof SND 2 2 z a2 n E 2 Always round up to the next larger whole number Find the sample size required to estimate the mean IQ of students currently taking a statistics course. Assume that we want 99% confidence that the mean from the sample is within two IQ points of the true population mean. Also assume that = 15 1. Use the range rule of thumb to estimate the standard deviation as follows: 2. Start the sample collection process without knowing σ and, using the first several values, calculate the sample standard deviation s and use it in place of σ. The estimated value of σ can then be improved as more sample data are obtained, and the sample size can be refined accordingly. 3. Estimate the value of σ by using the results of some other earlier study. Use Normal (z) distr. : is known and normally distributed population or n>30 Use t distribution: unknown and normally distributed population or n>30 Use nonparametric : population is not normally distributed and n<30 http://www.matematicasvisuales.com/english/html/probab ility/varaleat/tstudent.html