Download Slides 1-24 Estimation

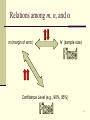
BA 275
Quantitative Business Methods
Agenda
 Statistical Inference: Confidence Interval Estimation
 Estimating the population mean m
 Margin of Error
 Sample Size Determination
 Examples
 Interval Estimation Using Statgraphics
1
Midterm Examination #1




Monday, January 29, 2007 in class for 110 minutes.
It covers materials assigned in Week 1 – 3.
Need a calculator and a good night sleep.
Close book/note/friends. I will provide you
1.
2.
3.
4.
the empirical rule (similar to Figure 1.21 on p. 58)
the standard deviation formula (p.41),
the CLT (p. 292), and
the normal probability table.
 Additional Office Hours
 Saturday, 1/27/07, 9:00 – 11:30 a.m.
 Monday, 1/29/07, 8:00 – 10:45 a.m.
2
Example 1
 A university administrator wanted to estimate
the average number of times students at her
university drank alcohol in the past month. A
random sample of 92 students was surveyed
by phone. The average number of times
students in the sample drank was 5.6 times
with a standard deviation of 6 times.
 Calculate a 95% confidence interval for the
average number of times all students at
the university drank alcohol in the past
month.
3
What does “95% confidence” mean?
“95% Confidence” is a short way of saying “We use a
method that gives correct results 95% of the time.”
4
Factors Affecting the Width
of a Confidence Interval
 Sample Size
 Confidence Level
Margin of error (m)
 Standard Deviation
X  z / 2

n
 X m
How good is your point estimate?
5
Relations among m, n, and 
m (margin of error)
N (sample size)
Confidence Level (e.g., 90%, 95%)
6
Estimation in Practice
 Determine a confidence level (say, 95%).
 How good do you want the estimate to be? (define
margin of error)
 Use the formula (p.371) to find out a sample size
that satisfies pre-determined confidence level and
margin of error.
 z / 2 
n
 for a " population mean" problem.
 m 
2
7
Example 2
 An auditor is sampling inventory items in
order to estimate the mean age of the items.
(a “population mean” problem!) The auditor
believes that the standard deviation is about
28. How large a sample is required to
estimate the mean age to within 1 day?
Assume that the confidence level is to be
99%.
8
Example 3
 An auditor is sampling inventory items in
order to estimate the mean age of the items.
(a “population mean” problem!) The auditor
believes that almost all of the ages will be
between 30 and 130 days. How large a
sample is required to estimate the mean age
to within 1 day? Assume that the confidence
level is to be 99%.
9
Sampling Distribution and CLT
An automatic machine in a manufacturing process is
operating properly if the lengths of an important
subcomponent are normally distributed, with mean
117 cm and standard deviation 5.2 cm.
1. Find the probability that one randomly selected
unit has a length greater than 120 cm.
2. Find the probability that, if four units are
randomly selected, their mean length exceeds
120 cm.
3. Find the probability that, if forty units are
randomly selected, their mean length exceeds
120 cm.
4. Without the assumption of normality, can we still
answer Questions 1 – 3.
10
Answer Key for Examples used
 Example 1.
5.6  1.96
6
6
, or 5.6  2
92
92
 Example 2. n   2.575  28   5198.41  5199
1


2
 Example 3.
130  30
 16.67
6
 2.575 16.67 
n
  1842.57  1843
1


2

Estimate  with

To be more conservative, estimate  with
, then
130  30
 25
4
, then
 2.575  25 
n
  4144.141  4145
1


2
 The CLT example

Q1: 0.281; Q2: 0.1251; Q3: 0.0000; Q4: Yes to all
because the population distribution is normal.
11