Estimation of Spatial Degrees of Freedom of a Climate
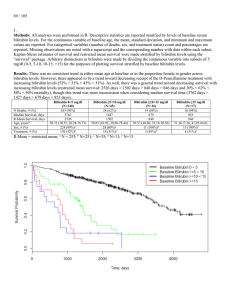
... [X] by using the binomial distribution (Livezey and Chen 1983). The sample statistic used in the B method is the ratio of the number of successful Bernoulli trials (m 0 , defined later) to the number of spatial points (N ). For a binomial distribution, B(n, p), an m can be decided for a given probab ...
... [X] by using the binomial distribution (Livezey and Chen 1983). The sample statistic used in the B method is the ratio of the number of successful Bernoulli trials (m 0 , defined later) to the number of spatial points (N ). For a binomial distribution, B(n, p), an m can be decided for a given probab ...
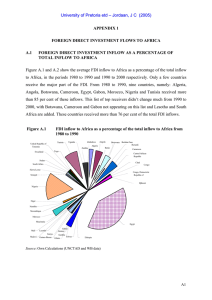
APPENDIX 1 FOREIGN DIRECT INVESTMENT FLOWS TO AFRICA A.1
... GNP is introduced to control for the size of the investing country, except when the sample covers only one investing country. Generally, larger countries are expected to invest abroad more than smaller ones. Recorded FDIs are pure financial flows. That is, they are neither equivalent to foreign fina ...
... GNP is introduced to control for the size of the investing country, except when the sample covers only one investing country. Generally, larger countries are expected to invest abroad more than smaller ones. Recorded FDIs are pure financial flows. That is, they are neither equivalent to foreign fina ...
Continuous Distributions
... Understand concepts of the uniform distribution. Appreciate the importance of the normal distribution. Recognize normal distribution problems and know how to solve such problems. Decide when to use the normal distribution to approximately binomial distribution problems and know how to work such prob ...
... Understand concepts of the uniform distribution. Appreciate the importance of the normal distribution. Recognize normal distribution problems and know how to solve such problems. Decide when to use the normal distribution to approximately binomial distribution problems and know how to work such prob ...
Experimental Design - People
... •The sampling distribution only approximates a normal curve when n gets big enough, over about 30. •Before that, the “tails" of the distribution are too big, so the estimated confidence interval is too small. •You can calculate the confidence intervals more precisely, but you need a separate table f ...
... •The sampling distribution only approximates a normal curve when n gets big enough, over about 30. •Before that, the “tails" of the distribution are too big, so the estimated confidence interval is too small. •You can calculate the confidence intervals more precisely, but you need a separate table f ...
Bootstrapping (statistics)

In statistics, bootstrapping can refer to any test or metric that relies on random sampling with replacement. Bootstrapping allows assigning measures of accuracy (defined in terms of bias, variance, confidence intervals, prediction error or some other such measure) to sample estimates. This technique allows estimation of the sampling distribution of almost any statistic using random sampling methods. Generally, it falls in the broader class of resampling methods.Bootstrapping is the practice of estimating properties of an estimator (such as its variance) by measuring those properties when sampling from an approximating distribution. One standard choice for an approximating distribution is the empirical distribution function of the observed data. In the case where a set of observations can be assumed to be from an independent and identically distributed population, this can be implemented by constructing a number of resamples with replacement, of the observed dataset (and of equal size to the observed dataset).It may also be used for constructing hypothesis tests. It is often used as an alternative to statistical inference based on the assumption of a parametric model when that assumption is in doubt, or where parametric inference is impossible or requires complicated formulas for the calculation of standard errors.