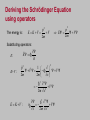Download 6. Quantum Mechanics II

CHAPTER 5
The Schrodinger Eqn.
5.1
5.2
5.3
5.4
5.5
The Schrödinger Wave Equation
Expectation Values
Infinite Square-Well Potential
Finite Square-Well Potential
Three-Dimensional InfinitePotential Well
5.6 Simple Harmonic Oscillator
5.7 Barriers and Tunneling
Erwin Schrödinger (1887-1961)
Homework due next Wednesday Sept. 30th
Read Chapters 4 and 5 of Kane
Chapter 4: 2, 3, 5, 13, 20 problems
Chapter 5: 3, 4, 5, 7, 8
problems
Stationary States
The wave function can now be written as:
( x, t )   ( x)eiEt /   ( x)eit
The probability density becomes:
*   * ( x) eit  ( x) eit
  ( x)
2
The probability distribution is constant in time.
This is a standing-wave phenomenon and is called a stationary state.
Most important quantum-mechanical problems will have stationary-state
solutions. Always look for them first.
Operators
d 2

 V  E
2
2m dx
2
The time-independent Schrödinger wave equation is as
fundamental an equation in quantum mechanics as the timedependent Schrödinger equation.
So physicists often write simply:
Ĥ  E
where:
2

Hˆ  
V
2
2m x
2
Ĥ is an operator yielding
the total energy (kinetic
plus potential energies).
Operators
 2 d 2 ( x)

 V ( x) ( x)  E ( x)
2
2m dx
Operators are important in quantum mechanics.
All observables (e.g., energy, momentum, etc.) have
corresponding operators.
The kinetic energy operator is:
2
K 
2m x 2
2
Other operators are simpler, and some just involve multiplication.
The potential energy operator is just multiplication by V(x).
Momentum Operator
To find the operator for p, consider the derivative of the wave function
of a free particle with respect to x:

 i ( kx t )

[e
]  ikei ( kx t )  ik
x x

 p
With k = p / ħ we have:
 i 
x
 
This yields:

p   i
x
This suggests we define the momentum operator as: pˆ  i
The expectation value of the momentum is:

p  i   * ( x, t )

 ( x, t )
dx
x

.
x
Position and Energy Operators
The position x is its own operator. Done.
Energy operator: Note that the time derivative of the free-particle
wave function is:
  i ( kx t )
 [e
]  iei ( kx t )  i
t
t
Substituting   E / ħ yields: E   i

t
This suggests defining the energy operator as:

Eˆ  i
t
The expectation value of the energy is:
E i
( x, t )
 ( x, t )
dx
t



*
Deriving the Schrödinger Equation
using operators
The energy is:
p2
 E 
 V 
2m
p2
E  K V 
V
2m
Substituting operators:
Ê   i
E:

t
pˆ 2
1 
 
  Vˆ  

i

  V 
2m
2m 
x 
2
K+V :
2

V 
2
2m x
2
E  K V :
2

 2
i

V 
2
t
2m x
Operators and Measured Values
In any measurement of the observable associated with an
operator A,
ˆ the only values that can ever be observed are the
eigenvalues. Eigenvalues are the possible values of a in the
Eigenvalue Equation:
Â  a
where a is a constant and the value that is measured.
For operators that involve only multiplication, like position and
potential energy, all values are possible.
But for others, like energy and momentum, which involve
operators like differentiation, only certain values can be the
results of measurements. In this case, the function  is often a
sum of the various wave function solutions of Schrödinger’s
Equation, which is in fact the eigenvalue equation for the energy
operator.
Solving the
Schrödinger
Equation when
V is constant.
When V0 > E:
d 2

 V0  E
2
2m dx
2
d 2 2m
Rearranging:
 2 V0  E 
2
dx
d 2
2

a

2
dx
where:
a  2m V0  E  /
2
Because the sign of the constant a2 is positive, the solution is:
kx
 kx
1
cosh(
kx
)

(
e

e
)
2
ax
a x
Sometimes
 ( x)  Ae  Be
When E > V0:
d 2
2


k

2
dx
people use: sinh( kx)  1 (e kx  e  kx )
2
where:
k  2m( E  V0 ) /
2
Because the sign of the constant k2 is negative, the solution is:
 ( x)  Aeikx  Beikx
or
A sin(kx)  B cos(kx)
Infinite Square-Well Potential
Consider a particle trapped in a box with
infinitely hard walls that the particle cannot
penetrate. This potential is called an infinite
square well and is given by:

V ( x)  
0
x  0, x  L
0  x  L
0
L
x
Outside the box, where the potential is infinite, the wave function must
be zero.
Inside the box, where the potential is zero, the energy is entirely kinetic,
E>V0
So, inside the box, the solution is:
 ( x)  A sin(kx)  B cos(kx)
Taking A and B to be real.
where
k  2mE /  2
Quantization and Normalization
Boundary conditions dictate that the wave
function must be zero at x = 0 and x = L.
This yields solutions for integer values of n
such that kL = np.
The wave functions  ( x)  A sin  np x 
n


are:
 L 
0
L
x
The same functions as those for a vibrating string with fixed ends!
In QM, we must normalize the wave functions:


 ( x)  n ( x) dx  1  A

*
n
The normalized wave
functions become:
2

L
0
½  ½ cos(2npx/L)
 np x 
sin 
 dx  1
 L 
 n ( x) 
2
2
 npx 
sin 

L
L


 A  2/ L
Quantized Energy
We say that k is quantized:
Solving for the energy yields:
kn 
2mEn
np

L
2
En  n
2
p2
2
2
2mL
(n  1, 2, 3,...)
The energy also depends on n. So the energy is also quantized.
The special case of
n = 1 is called the
ground state.
E1 
p 2 2
2mL2
Finite Square-Well
Potential
The finite square-well potential is:
V0

V ( x)   0
V
 0
x  0
Region I
0  x  L Region II
x  L
Region III
Assume:
E < V0
The solution outside the finite well in regions I and III, where E < V0, is:
Region I, x  0
 I ( x)  Aea x
 III ( x)  Bea x Region III, x  L
Realizing that the wave function must be zero at x = ±∞.
Finite Square-Well Solution (continued)
Inside the square well, where the potential V is zero, the solution is:
 II ( x)  C sin kx  D cos kx Region II, 0  x  L
Now, the boundary conditions
require that:
 I   II at x  0
 II   III at x  L
So the wave function is smooth
where the regions meet.
Note that the wave function is
nonzero outside of the box!
The particle penetrates the walls!
This violates classical
physics!
The penetration depth is
the distance outside the
potential well where the
probability decreases to
about 1/e. It’s given by:
x
1
a

2m(V0  E )
Note that the penetration
distance is proportional to
Planck’s constant.
Barriers and Tunneling
Consider a particle of energy E approaching a potential barrier of
height V0, and the potential everywhere else is zero and E > V0.
In all regions, the solutions are sine waves. In regions I and III, the
values of k are:
2mE
k I  k III 
2m( E  V0 )

In the barrier region: kII 