* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Electromagnetism - Lecture 4 Dipole Fields
Magnetic field wikipedia , lookup
Electric charge wikipedia , lookup
Magnetic monopole wikipedia , lookup
Electromagnetism wikipedia , lookup
Superconductivity wikipedia , lookup
Electromagnet wikipedia , lookup
Maxwell's equations wikipedia , lookup
Lorentz force wikipedia , lookup
Circular dichroism wikipedia , lookup
Aharonov–Bohm effect wikipedia , lookup
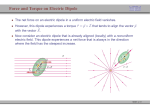
Electromagnetism - Lecture 4 Dipole Fields • Electric Dipoles • Magnetic Dipoles • Dipoles in External Fields • Method of Images • Examples of Method of Images 1 Electric Dipoles An electric dipole is a +Q and a −Q separated by a vector a Very common system, e.g. in atoms and molecules The electric dipole moment is p = Qa pointing from −Q to +Q Potential of an electric dipole: 1 1 Q(r− − r+ ) Q − = V = 4π0 r+ r− 4π0 r+ r− Using cosine rule, where r is distance from centre of dipole: 2 r± a2 ∓ ar cos θ =r + 4 2 and taking the “far field” limit r >> a p.r̂ Qa cos θ = V = 2 4π0 r 4π0 r 2 2 Electric Dipole Field Components of the electric field are derived from E = −∇V In spherical polar coordinates: 2p cos θ ∂V = Er = − ∂r 4π0 r 3 Eθ = − p sin θ 1 ∂V = r ∂θ 4π0 r 3 In cartesian coordinates, where the dipole axis is along z: p(3 cos2 θ − 1) Ez = 4π0 r 3 Ex/y = 3p cos θ sin θ 4π0 r 3 Electric dipole field decreases like 1/r 3 (for r a) 3 Notes: Diagrams: 4 Magnetic Dipoles A bar magnet with N and S poles has a dipole field A current loop also gives a dipole field Example: atomic electrons act as current loops Think of current elements +Idl and −Idl on opposite sides of the current loop as equivalent to +Q and −Q The magnetic dipole moment points along the axis of the loop Direction relative to Idl is given by corkscrew rule m = Iπa2 ẑ = IAẑ For a current loop m is the product of current times area Magnetic dipole field has the same shape as electric dipole field: 2µ0 m cos θ Br = 4πr 3 µ0 m sin θ Bθ = 4πr 3 5 Dipoles in External Fields An External Field is provided by some large and distant charge (or current) distribution Usually assumed to be uniform and constant, i.e. it is not changed by any charges or currents that are inserted in it An electric dipole in a uniform electric field E0 aligns itself with the external field with p || E Work needed to reverse direction of dipole: ∆U = W+ + W− = 2QaE0 = 2pE0 6 Torque and Energy of Dipoles Consider electric dipole at angle θ to external electric field E0 Torque acting to rotate the dipole into alignment with the field: T = QaE0 sin θn̂ = p × E The work done during this rotation is: Z Z W = T dθ = pE0 sin θdθ = pE0 cos θ Potential energy of an electric dipole in an external electric field: U = −p.E Similar results for a magnetic dipole in an external magnetic field: U = −m.B T=m×B 7 Notes: Diagrams: 8 Method of Images A point charge +Q is a distance a from a flat conducting surface Boundary conditions: E|| = 0 at the conducting surface but E⊥ = σ/0 is allowed at the surface A simple point charge field does not satisfy these conditions! ⇒ but a dipole field centred on the surface does Method of images: Put an image charge −Q a distance −a behind the surface Note that this charge does not actually exist! Calculate the dipole field from the +Q and −Q and show that it satisfies the boundary conditions 9 Electric Field at Conducting Surface Using the method of images the field at the conducting surface is the z component of a dipole field at θ = 90◦ : 2Qa(3 cos2 θ − 1) −Qa = Ez = 4π0 r 3 2π0 (x2 + y 2 )3/2 This field must be produced by a surface charge density σ: σ Ez = 0 σ= −Qa 2π(x2 + y 2 )3/2 There is no electric field inside the conductor E(z < 0) = 0 The distribution of σ on the surface has exactly the same effect as R a −Q placed at −a (can show that σdS = −Q) Note that there is an attractive force between +Q and the surface 10 Notes: Diagrams: 11 Notes: Diagrams: 12 Conducting Sphere in External Field Boundary conditions: Eθ = 0 at the spherical surface but Er = σ/0 is allowed at the surface A uniform external field E0 does not satisfy these conditions! Think what would happen to a surface charge distribution: +σ will prefer to be on one side of the sphere −σ will prefer to be on the other side of the sphere The sphere becomes polarized with a dipole moment p Hypothesis: the polarization of the sphere can be represented by an electric dipole at its centre The electric field at the surface is the sum of the uniform external field and the dipole field 13 Electric Field at Surface of Sphere Potential is superposition of uniform and dipole potentials: V = −E0 r cos θ + p cos θ + V0 2 4π0 r The spherical surface r = R must be an equipotential V = V0 p = 4π0 R3 E0 = 30 E0 VS Dipole moment depends on E0 and volume of sphere VS Note that this works for all cos θ! The surface charge density depends on E0 and cos θ: 2p cos θ ) = 30 E0 cos θ σ = 0 Er = 0 (E0 cos θ + 4π0 R3 From cos θ there is +σ in the right hemisphere and −σ in the left hemisphere. 14 Notes: Diagrams: 15 Notes: Diagrams: 16