Download Slides - GSI IndiCo

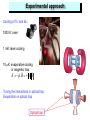
Cold Gases Meet
Condensed Matter Physics
C. Salomon
Laboratoire Kastler Brossel,
Ecole Normale Supérieure & UPMC, Paris, FR
EMMI, GSI, Darmstadt, July 17th, 2008
Temperature scale of cold gases
this
room
liquid liquid
sun
He
N2
surface
cold
atomic
gases
1 mK
1 mK
1K
100 K
104K
sun
center
106K
quark-gluon plasma
Dilute, but interacting systems
1012 K
Typical density:
Interatomic distance
range of interatomic potentials
quantum of the motion in the trap
thermal energy
Equilibrium properties and dynamics are governed by interactions
T
Quantum gases in harmonic traps
Bose-Einstein statistics (1924)
Bose-Einstein condensate
Fermi-Dirac statistics (1926)
Fermi sea
EF
Bose enhancement
h

1
/
3
T
=
(
0
.
8
3
N
)
C
k
B
Dilute gases: 1995, JILA, MIT
Pauli Exclusion
h
 1
/
3
T
<
<
T
=
(
6

N
)
F
k
B
Dilute gases: 1999, JILA
Quantum gases : orders of magnitude
Dilute gaz at temperature T
confined in harmonic trap :
1
V (r )  m 2 r 2
2
Condensation threshold:
3
 k BT 
N  1.202 




kBT
Liquid Helium :
1027
atoms/m3
n0-1/3 = 10 Å
T ~1 K

n0 : central density
n0 3  2.612
h

2 mk BT
Gaseous condensate:
1019 atoms/m3
n0-1/3 = 0.5 mm
T ~1 mK
Absorption imaging
in situ: cloud size
After switching off the trap: momentum distribution
Bose-Einstein condensate and Fermi sea
Lithium 7
2001
ENS
Lithium 6
104 Li 7 atoms, in thermal equilibrium with
104 Li 6 atoms in a Fermi sea.
Quantum degeneracy: T= 0.28 mK = 0.2(1) TC= 0.2 TF
Interest of cold gases
Diluteness: atom-atom interactions described by 2-body (and 3 body) physics
At low energy: a single parameter, the scattering length
Control of the sign and magnitude of interaction
Control of trapping parameters:
access to time dependent phenomena, out of equilibrium situations,
1D, 2D, 3D
Simplicity of detection
n(k)
n(k)
Comparison
with theory:
1
Gross-Pitaevskii,
Bose and Fermi Hubbard models,
1
search for exotic phases, disorder effects,…
Link with condensed matter (high Tc superconductors, magnetism in lattices),
nuclear physics, high energy physics (quark-gluon plasma),
and astrophysics (neutron stars)
k/kF
1
k/kF
1
Towards quantum simulation with cold atoms « a la Feynman »
This talk
3 examples of the physics of strongly correlated systems
Tuning atom-atom interactions:
n(k)
1)
n(k)
Superfluidity in strongly interacting Fermi gas: a high Tc system
1
1 the trapping potential:
Tuning
2) The Mott-Insulator transition in a 3D periodic potential
3) Superfluidity in 2D Bose gas: the Berezinski-Kosterlitz-Thouless transition
1
1
k/kF
k/kF
Fermi superfluid and Bose-Einstein condensate of Molecules
Fermions with two spin states with attractive interaction
BEC of molecules
Bound state
BCS fermionic superfluid
Interaction strength
No bound state
Dilute gases: Feshbach resonance
n(k)
n(k)
1
1
Tuning atom-atom interactions
1
1
k/kF
k/kF
Atom-atom interactions
At low T, interactions are characterized by the s wave scattering length a
a/b
|U’> + |U’>
1
n-1
bound
states
n
bound
states
n+1
bound
states
r
|U> + |U>
A Fano-Feshbach resonance brings a new (closed) channel in the
collision process, and it “mimicks” the entrance of a new bound state.
C6
a0
EB=-h2/ma2
a
scattering length [nm]
200
100
0
-100
a0
-200
0,0
0,5
1,0
1,5
Magnetic field [kG]
2,0
Lithium 6 Feshbach resonance
interacting fermions
scattering length [nm]
200
100
BEC-BCS
Crossover
0
-100
-200
0,0
Bound state
0,5
1,0
1,5
Magnetic field [kG]
2
Eb
ma2
condensate of molecules
2,0
No bound state
BCS phase
Experimental approach
Cooling of 7Li and 6Li
1000 K: oven
1 mK: laser cooling
10 mK: evaporative cooling
in magnetic
 trap 


E   m.B   m B
Tuning the interactions in optical trap
Evaporation in optical trap
Optical trap
Condensates of molecules
JILA: 40K2
MIT
6Li
2
6Li :Innsbruck
2
ENS
6Li
2
6Li
2
Also Rice, Duke, Tokyo, Swinburne, 6Li2
7Li
Experiments on BEC-BCS crossover
Interaction between molecules and lifetime of molecules
Unitarity regime: kFa>>1 ?
Probing fermionic superfluidity
Momentum distribution of particles
Superfluidity with imbalanced Fermi spheres
Can we measure the excitation gap ?
A high temperature superfluid: Tc=0.2 TF
JILA, Innsbruck, MIT, ENS, Rice, Duke, Swinburne, Tokyo,…
Universal equation of state of
the unitary Fermi gas
Balanced Fermi gas ( m  m )
1  2 mm 
n 2 2 
6 

m  
Theory
2
6 n 

2m
2
3/ 2
x numerical factor
First example of a quantum simulator !
2/3
  EF
Determination of 
ENS (6Li)
0.42(15)
0.42(1)
Rice (6Li)
0.46(5)
Perali
0.455
JILA(40K)
0.46(10)
Carlson
0.42(1)
Innsbruck (6Li)
0.27(10)
Haussmann
0.36
Duke (6Li)
0.51(4)
BCS
0.59
Astrakharchik
Experiment
Direct proof of superfluidity:
classical vs. quantum rotation
Rotating classical gas
velocity field of a rigid body
Rotating a quantum macroscopic object
macroscopic wave function:
In a place where
, irrotational velocity field:
The only possibility to generate a non-trivial rotating motion is to nucleate
quantized vortices (points in 2D or lines in 3D)
Feynman, Onsager
Vortices now all have the same sign, imposed by the external rotation
MIT 2005: Vortex lattices in the BEC-BCS Crossover
Energy [MHz]
1
Direct proof of superfluidity
0
BEC side
BCS side
M. Zwierlein
A. . Schirotzek
C. Stan
C. Schunk
P. Zarth
W. Ketterle
Science 05
-1
650
834.15
Magnetic Field [G]
MIT 2005
Superfluidity in a freely expanding gas !
2: Creating artificial crystals
Periodic optical potential
A laser beam (far detuned from resonance to avoid spontaneous emission)
creates a conservative potential on the atoms:
typical depth: microkelvin to millikelvin
Optical lattice: periodic potential
created by interfering beams
Here period: 27mm
Cs atoms in an optical lattice
ENS, 1998
A Bose-Einstein condensate in a lattice
tunnelling
if tunnelling is large enough, the
coherence between the microBECs
at each site is maintained
Time-of-flight experiment:
• release the atoms from the lattice
• let the various clouds overlap
time of
optical
lattice
flight
I. Bloch et al., 2002
Constructive interference as for Bragg diffraction by a grating
The superfluid – Mott insulator transition
Large lattice depth: repulsive interactions dominate over tunnelling
The system evolves to a state with a fixed number of atoms/site
Bose-Hubbard problem
Fisher et al. 1989,
Jaksch et al. 1998
V0 = 10 Er
Munich 2002
V0 = 13 Er
V0 = 16 Er
coherence
is lost!
Next challenge:
produce antiferromagnetic order
• First step: generate an interaction
between adjacent sites?
Use atoms with a large dipole (chromium, Stuttgart)
Use ground state polar molecules
Use Pauli principle + on-site interactions: super-exchange
Observed in a double well potential by the Mainz group (2007)
• Second step: achieve a low enough temperature in a lattice:
: spin up
: spin down
Square lattice:
Néel ordering
Triangular lattice:
frustration
3: Cold gases in low dimensions
Two-dimensional Quantum Physics
Quantum wells and MOS structures
High Tc superconductivity
also Quantum Hall effect, films of superfluid helium, …
Key words of two-dimensional physics:
• absence of true long range order (no BEC stricto sensu)
• existence of a new kind of phase transition (Kosterlitz-Thouless)
• No spin-statistics theorem, and existence of parastatistics: any-ons
• Non abelian physics: towards topological quantum computing ??
The Berezinski-Kosterlitz-Thouless mechanism
1971-73, 2D gas of bosons
0
Tc
superfluid
normal
exponential decay of g1
algebraic decay of g1
Microscopic origin of this phase transition: quantized vortices
Vortex: point where
, around which
Around a vortex:
rotates by
T
Superfluidity in
in 22D:
However: Superfluidity
dimensions
Berezinski-Kosterlitz-Thouless Mechanism
Berezinski and Kosterlitz –Thouless 1971-73
0
superfluid
Tc
normal
Unbinding of
Bound vortexantivortex pairs
vortex pairs
Proliferation of
free vortices
Superfluid transition observed with
liquid helium films by Bishop-Reppy, 1978
T
Producing
a cold 2D gas
Producing
a 2 Dimensional
Cold Gas
2D experiments at MIT, Innsbruck, Oxford, Florence, Boulder,
Heidelberg, Gaithersburg, Paris (Dalibard’s group)
Paris: superposition of a
harmonic magnetic potential
+
periodic potential of
a laser standing wave
Two
independent
planes
Time of
flight
2D physics revealed by matter-wave interferometry
ENS Dalibard group
cold
hot
sometimes: dislocations!
fraction of images
showing a dislocation

0
Dislocation
=
evidence for
free vortices
0.4
0.3
0.2
0.1
0.5
0.75
1
temperature
control
(arb.units)
uniform phase 0
Prospects
With cold atoms, one can simulate several many-body Hamiltonians
• Bosons, fermions, and mixtures
• Pairing with mismatched Fermi spheres, exotic phases
• Periodic potential or disordered (Anderson localization)
• Gauge field with rotation or geometrical phase
• Non abelian Gauge field for simulating the Hamiltonian
of strong interactions in particle physics
• Quantum Hall physics and Laughlin states
New experimental methods:
• Image a many-body wavefunction with micrometer resolution
• Measure correlation functions
• Photoemission spectroscopy to measure Fermi surface
and single particle excitations
• Time-dependent phenomena in 1, 2, and 3 D
BEC of Molecules
Method
a<0
a>0
EB  
2
/ ma
JILA
ENS
Ekin
2
Bo
B
BEC of molecules
Recipe: in region a<0, cool a gas of fermions below 0.2TF
Slowly scan across resonance towards a>0
Typically : 1000 G to 770 G in 200 ms
This produces molecules with up to 90% efficiency !
Reversible process ! Entropy is conserved.
If T< 0.2 TF, BEC of molecules