Download Physics in Ultracold atoms

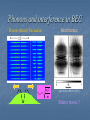
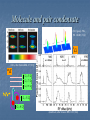
World of ultracold atoms
with strong interaction
Daw-Wei Wang
National Tsing-Hua University
Temperature ?
What we mean by “ultracold” ?
T  106 K !
Why low temperature ?
Ans: To see the quantum effects !
Uncertainty principle: xp 
p 2
~ kBT  x ~
~
 T , Thermal wavelength
2m
p
2mkBT
Therefore, if T   T 
Quantum regime when T  d ~ n 1/ 3
T
d
(after Nature, 416, 225 (’02))
Why strong interaction ?
P. Anderson: “Many is not more”
Because interaction can make
“many” to be “different” !
Example: 1D interacting electrons
 crystalization and no fermionic excitation
How to make interaction stronger ?
 p 2j
 1 N
H  
 V ( x j )    U ( xi  x j )

 2 i j
j 1  2m

N
1. U ( x) becomes stronger
2. Ek ~ k BT becomes smaller or m becomes smaller
3. V ( x) changes to make lower dimension
4. N becomes larger (for short interactio n);
smaller for long range interactio n
How to reach ultracold temperature ?
1. Laser cooling !
(1997 Nobel Price)
Use red detune laser
+ Doppler effect
How to reach ultracold temperature ?
2. Evaporative cooling !
Reduce potential barrial
+thermal equilibrium
Typical experimental environment
MIT
How to do measurement ?
Trapping and cooling
Perturbing
Releasing and measuring
BEC
(2001 Nobel Price)
What is Bose-Einstein
condensation ?
( x1 , x2 )  ( x2 , x1 ), + for boson and - for fermion
Therefore, for fermion we have ( x, x)  0,
i.e. fermions like to be far away,
but bosons do like to be close !
When T is small enough,
noninteracting bosons
like to stay in the lowest
energy state, i.e. BEC
How about fermions in T=0 ?
D(E)
Fermi sea
E
When T-> 0, noninteracting
fermions form a compact
distribution in energy level.
BEC and Superfluidity of bosons
(after Science, 293, 843 (’01))
condensate
BEC = superfluidity
v
repulsion
Superfluid
uncondensate
Normal fluid
Landau’s two-fluid model
Phonons and interference in BEC
Phonon=density fluctuation
n0U
v ph 
m
Interference
(after Science 275, 637 (’97))
Matter waves ?
Vortices in condensate
Vortex = topological disorder
E
0
(after Science 292, 476 (’01))
(after PRL 87, 190401 (’01))
1
2
3
L
En,l  0 l  3n  2nl  2n2  lext
Vortices melting, quantum Hall regime ?
Spinor condensation in optical trap
Na F  1, mF  1,0
E
F=2
F=1
FIJ
B
(see for example, cond-mat/0005001)
2


g0  
g2 
 

ˆ
ˆ
ˆ
ˆ
ˆ
ˆ
ˆ
ˆ
ˆ
ˆ
H   dr  i
 i   i  j j i   i Fij j   k Fkl l 
2m
2
2


Boson-fermion mixtures
Fermions are noninteracting !
phonon
fermion
phonon-mediated interaction
40
K 87Rb, 6Li7Li, or 6Li23Na
D(E)
rf-pulse
Interacting
fermi sea
E
Sympathetic cooling
Feshbach Resonance
(i) Typical scattering:

B 

a  a0 1 
 B  B0 
(ii) Resonant scattering:
a
B
Molecule state
Molecule and pair condensate
(MIT group, PRL
92, 120403 (’04))
6
Li
(JILA, after Nature 424, 47 (’03))
40
K
9 / 2,5 / 2
9 / 2,7 / 2
9 / 2,9 / 2
9 / 2,5 / 2
9 / 2,9 / 2
(Innsbruck, after Science 305, 1128 (’04))
First evidence of superfluidity of fermion pairing
a
B
Optical lattice
3D lattice
1D lattice
 R (  E )
2
V0  
Entanglement control

E
other lattice
  E 2  2
Mott-Insulator transition
Bose-Hubbard model
H  t  ai a j  U  ai ai (ai ai  1)    ai ai
i , j 
i

i
n=3
superfluid
n=2
n=1
t /U
(after Nature 415, 39 (’02))
Fermions in optical lattice
Fermi Hubbard model
H  t  ai, s a j , s  U  ni , ni ,
i , j 
i
Superfluidity of fermion pairing in lattice is also realized.
Transport in 1D waveguide
wave guide
wire
Interference ?
Finite temperature
+ semiconductor technique
Dipoles in nature:
(1) Heteronuclear molecules
(2) Atoms with large
magnetic moment
(a) Direct molecules
p~ 1-5 D
(b) But difficult to be cooled
Small moment  ~ 6 (for Cr)
B
(Doyle, Meijer, DeMille etc.)
But it is now ready to go !
(Stuhler etc.)
p ~ 1D, Udd ~ 10K,   1B , Udd ~ 1nK
Condensate (superfluid)
  6B
Tc~700 nK
Cold dipolar atoms/molecules
(1) Heteronuclear molecules
(2) Atoms with large
magnetic moment
(a) Direct molecules
p~ 1-5 D
(b) But difficult to be cooled
Small moment  ~ 6 (for Cr)
B
(Doyle, Meijer, DeMille etc.)
But it is now ready to go !
(Stuhler etc.)
p ~ 1D, Udd ~ 10K,   1B , Udd ~ 1nK
Condensate (superfluid)
  6B
Tc~700 nK
Interdisciplinary field
Traditional
AMO
Precise
measurement
Ultracold atoms Quantum Information
Nonlinear
Physics
Condensed matter
Soft-matter/
chemistry