Download Second-order dynamic circuits

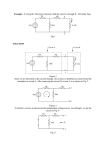
1
Second-order dynamic circuits
Dynamic circuits containing two capacitors or two inductors or one inductor and one
capacitor are called second-order circuits. In this section we learn how to formulate the
equation governing such circuits.
Linear circuits
Two–capacitor configuration
Let us consider a circuit containing linear resistors, linear controlled sources, independent
sources and two capacitors. We extract both capacitors from the circuit creating a linear
resistive two-port LRTP as shown in Fig. 1.
i1
i2
iC2
iC1
C1
vC1
LRTP
v1
C2
v2
vC2
Fig. 1
We choose capacitor voltages vC1  v1 and vC2  v 2 as state variables and write a system of
two first-order differential equations
C1
C2
dvC1
dt
dv C 2
dt
 iC1  i1 ,
(1)
 iC 2  i 2 ,
where i1 and i2 are the port currents. Since the port currents are not state variables, we express
them in terms of vC1  v1 and vC2  v 2 . For this purpose we terminate the two-port by voltage
sources v1 and v2 (see Fig. 2) and solve the circuit for the port currents i1 and i2.
i2
i1
v1
LRTP
Fig. 2
v2
2
To find i1 and i2 we apply the superposition theorem. First we consider the circuit driven by
the voltage source v1 acting alone. Thus, we set to zero the voltage source v2 and all the
independent sources inside the LRTP. As a result we obtain the circuit shown in Fig. 3.
~
i2
~
i1
LRTP
without
independent
sources
v1
Fig. 3
~
~
In this circuit the currents i1 and i2 are given by the equations
~
i1  g11v1 ,
~
i2  g 21v1 ,
(2)
where g11 and g21 are constants.
Next we consider the circuit driven by the voltage source v2 acting alone (see Fig.4) and solve
~
~
~
~
it for i1 and i2
~
~
i2
~
~
i1
LRTP
without
independent
sources
v2
Fig. 4
As a result we find
~
~
i1  g12 v 2 ,
~
~
i2  g 22 v2 ,
(3)
where g12 and g22 are constants.
Finely we set to zero v1 and v2 and consider the circuit driven by the independent sources
inside the LRTP (see Fig. 5). We solve this circuit for the port currents iS1 and iS2 .
3
i S2
i S1
LRTP
Fig. 5
According to the superposition theorem we write
~ ~
~
i1  i1  i1  i S1  g11v1  g12 v 2  iS1 ,
~ ~
~
i2  i2  i2  iS2  g 21v1  g 22 v 2  iS2 .
(4)
Substituting equations of the set (1) in place of i1 and i2 and replacing v1 and v2 by
vC1 and v C2 we obtain, after simple rearrangement, the state equations describing the circuit
shown in Fig. 1
dvC1
dt

1
1
1
g11vC1  g12 vC2  iS1 ,
C1
C1
C1
(5)
dv C 2
1
1
1

g 21vC1 
g 22 vC2 
iS ,
dt
C2
C2
C2 2
where i S1 and i S2 are generally time-varying currents. The system of equations (5) can be
presented in matrix form
dvC
 AvC  bt  ,
dt
(6)
where
 1


 dvC1 
  C iS1 

 vC1  dv


d
t
1
C
, A
 , bt   
vC    ,

d
v
1
d
t





vC 2 
C2
  C iS 2 

 dt 

2


To illustrate the described approach we consider a simple example.
Example 1
Given the second-order circuit shown in Fig. 6
g11
C1
g 21
C2
g12 
C1 
.
g 22 

C2 

4
R1
i1
R2
C1 v1
vC1
i2
v2 C2
R3
vC2
Fig. 6
To formulate the state equations describing this circuit we consider the linear resistive oneport consisting of resistors R1, R2, and R3, terminated by voltage sources v1 and v2 as shown in
Fig. 7. We solve this circuit for i1 and i2 using the superposition theorem.
R1
R2
i2
i1
v1
R3
v2
Fig. 7
First we set v2 = 0 and analyse the circuit shown in Fig. 8.
~
i1
R1
R2
v1
~
2
R3
Fig. 8
As a result we obtain
~
i1 
v1
,
R2 R3
R1 
R2  R3
~
~
i2   i1
R3
R3 v1

.
R2  R3
R1 R2  R1 R3  R2 R3
Thus we have
~
i1  g11 v1 ,
g 11 
1
,
R 2 R3
R1 
R2  R3
(7)
5
~
i2  g 21v1 ,
g 21  
R3
.
R1 R2  R1 R3  R2 R3
(8)
Next we set v1 = 0 and analyse the circuit shown in Fig. 9.
~
~
i1
R1
R2
~
~
i2
R3
v2
Fig. 9
As a result we obtain
~
~
i2 
v2
,
RR
R2  1 3
R1  R3
~
~
~
~
i1   i2
R3
R3 v2

.
R1  R3
R2 R1  R2 R3  R1 R3
Hence, we have
~
~
i1  g12 v 2 ,
g12  
~
~
i2  g 22 v 2 ,
R3
,
R2 R1  R2 R3  R1 R3
g 22 
1
.
R1 R3
R2 
R1  R3
(9)
(10)
According to the superposition theorem we write
i1  g11v1  g12 v 2 ,
i2  g 21v1  g 22 v 2 .
Since
dvC1
dv1
 C1
,
dt
dt
dvC 2
dv
i2  C 2 2  C 2
,
dt
dt
i1  C1
and v1  vC1 , v 2  vC2 , we obtain after simple rearrangements the state equations
(11)
6
dvC1
dt

g11
g
vC1  12 v C2 ,
C1
C1
(12)
dv C 2
g
g
  21 vC1  22 vC2 ,
dt
C2
C2
where g11, g21, g12, g22 are given by (7)-(10).
Two–inductor configuration
Let us consider a circuit containing linear resistors, linear controlled sources, independent
sources and two inductors. We extract both inductors from the circuit creating a linear
resistive two-port (LRTP) as shown in Fig. 10.
i2
i1
vL1
L1
LRTP
v1
v2
iL1
L2
vL2
L2
Fig.10
We choose inductor currents i L1  i1 and i L2  i2 as state variables and write a system of two
first-order differential equations
L1
L2
di L1
dt
di L2
dt
 v L1  v1 ,
(13)
 v L2   v 2 ,
where v1 and v2 are the port voltages. Since v1 and v2 are not state variables, we express them
in terms of i L1 and i L2 . For this purpose we terminate the two-port by current sources i1 and i2
(see Fig. 11) and solve the circuit for the port voltages v1 and v2.
i1
v1
LRTP
Fig. 11
v2
i2
7
To find v1 and v2 we apply the superposition theorem. First we consider the circuit driven by
the current source i1 acting alone. Thus, we set to zero the current source i2 and all the
independent sources inside the LRTP. As a result we obtain the circuit shown in Fig. 12.
i1
~
v1
v
LRTP
without
independent
sources
~
v2
Fig. 12
In this circuit the voltages
v~1 and ~
v2 are given by the equations
v~1  r11i1 ,
v~  r i ,
2
(14)
21 1
where r11 and r22 are constants.
Next we consider the circuit driven by the current source i2 acting alone (see Fig. 13) and
~
~
solve it for v~1 and v~2 .
~
v~1
LRTP
without
independent
sources
~
~
v2
i2
Fig. 13
As a result we find
~
v~1  r12 i2 ,
~
v~2  r22 i2 ,
where r12 , r22 are constants.
Finally we set to zero i1 and i2 and consider the circuit driven by the independent sources
inside the LRTP (see Fig. 14). We solve this circuit for the port voltages v S1 and v S2 .
8
vS1
LRTP
vS 2
v
Fig. 14
According to the superposition theorem we write
v1  v~1  v~2  v S1  r11i1  r12 i2  v S1 ,
~
v2  ~
v2  v~2  v S2  r21i1  r22 i2  v S2 .
(15)
Substituting the equations (13) in place of v1 and v2 and replacing i1 and i2 by i L1 and i L2 we
obtain, after simple rearrangement, the state equations describing the circuit shown in Fig. 10.
di L1
dt

r11
r
1
i L1  12 iL2  v S1 ,
L1
L1
L1
di L2
(16)
r
r
1
  21 i L1  22 iL2  v S2 ,
dt
L2
L2
L2
where v S1 and v S2 are generally time varying voltages.
The system of equations (16) can be presented in matrix form
di L
 Ai L  b( t ) ,
dt
where

 diL1 

iL1  diL  dt 
 , bt   
iL    ,

i
d
i
d
t


L2 
 L2 

 dt 

1
r 

 r11
vS1 

 12 

L1
L
L1
 , A 1
.
1
r22 

 r21
vS
 L  L 
L2 2 
 2
2
Example 2
Let us consider the second-order circuit shown in Fig. 15
(17)
9
R1
i1
vL1
R2
L1 v1
R3
i2
vL2
v2 L2
iL2
iL1
Fig. 15
To formulate state equations describing this circuit we consider the linear resistive one-port
consisting of the resistors R1, R2, and R3, terminated by current sources i1 and i2 as shown in
Fig. 16. We solve this circuit for v1 and v2 using the superposition theorem.
R1
i1
R2
R3
v1
i2
v2
Fig. 16
First we set i2 = 0 and analyse the circuit shown in Fig. 16.
R1
R2
~
i2  0
i1
v~1
R3
~
v2
Fig. 17
As a result we obtain
v~1  R1  R3 i1 ,
v~2  R3i1 .
Thus, we have
v~1  r11i1 ,
v~2  r21i1 ,
r11  R1  R3 ,
(18)
r21  R3 .
(19)
Next we set i1 = 0 and analyse the circuit shown in Fig. 18.
10
~
~
i1  0
R1
R2
~
~
v1
R3
~
~
v2
i2
Fig. 18
As a result we obtain
~
v~1  R3i2 ,
~
v~2   R2  R3 i2 .
Thus, we have
~
v~1  r12 i2 ,
~
v~2  r22 i2 ,
r12  R3 ,
(20)
r22  R2  R3 .
(21)
According to the superposition theorem we write
v1  r11i1  r12 i2 ,
v2  r21i1  r22 i2 .
Since
di L
di1
  L1 1 ,
dt
dt
di L
di
v2   L2 2   L2 2 ,
dt
dt
v1   L1
and i1  i L1 , i2  i L2 , we obtain after simple rearrangements the state equations
diL1
dt

r11
r
i L1  12 i2 ,
L1
L1
diL2
(22)
r
r
  21 iL1  22 i2 ,
dt
L2
L2
where r11, r21, r12, r22 are given by (18) – (21).
Capacitor–inductor configuration
Circuits containing one capacitor, one inductor, linear resistors, linear controlled sources
and independent sources can be presented in the form shown in Fig. 19.
11
i1
i2
iC1
vC1
C1
LRTP
v1
L2
v2
vL2
L2
Fig. 19
We choose the capacitor voltage vC1  v1 and the inductor current iL2  i2 as state variables
and write a system of two first-order differential equations
C1
L2
dvC1
dt
diL2
dt
 iC1  i1 ,
(23)
 v L2  v 2 ,
where i1 is the port current and v2 is the port voltage. To express i1 and v2 in terms of the state
variables vC1  v1 and iL2  i2 we terminate the LRTP by voltage source v1 and current source
i2 (see Fig. 20) and solve the circuit for i1 and v2.
i1
v1
LRTP
v2
i2
Fig. 20
To find i1 and v2 we apply the superposition theorem. First we consider the circuit driven by
the voltage source v1 acting alone as shown in Fig. 21.
~
~
i1
i2  0
v1
LRTP
without
independent
sources
Fig. 21
~
In this circuit the current i1 and the voltage v~2 are given by the equations
v~2
12
~
i1  f11v1 ,
v~  f v ,
2
(24)
21 1
where f11 and f21 are constants.
Next we consider the circuit driven by the current source i2 acting alone (see Fig. 22) and
~
~
~
solve it for i and ~
v .
1
2
~
~
i1
LRTP
without
independent
sources
~
~
v2
i2
Fig. 22
As a result we find
~
~
i1  f12 i2 ,
~
v~  f i ,
2
(25)
22 2
where f12, f22 are constants.
Finally we set to zero v1 and i2 and consider the circuit driven by the independent sources
inside the LRTP (see Fig. 23). We solve this circuit for iS1 and v S2 .
iS1
LRTP
vS 2
Fig. 23
According to the superposition theorem we write
~ ~
~
i1  i~1  i1  iS1  f11v1  f12 i2  iS1 ,
~
v2  v~2  ~
v2  v S2  f 21v1  f 22 i2  v S2 .
Substituting the equations (23) in place of i1 and v2 yields
(26)
13
dvC1

dt
f11
f
1
vC1  12 iL2  iS1 ,
C1
C1
C1
(27)
diL2
f
f
1
  21 vC1  22 i L2  v S2 ,
dt
L2
L2
L2
where iS1 and v S2 are generally time-varying signals.
Example 3
Consider the second-order circuit shown in Fig. 24.
R1
i1
vC1
R2
C1 v1
i2
R3
vL2
v2 L2
L2
Fig. 24
To formulate state equations describing this circuit we take into account the linear resistive
two-port consisting of R1, R2, R3 terminated by voltage source v1 and current source i2 as
shown in Fig. 25
R1
R2
i1
v1
R3
i2
v2
Fig. 25
We solve this circuit for i1 and v2 using the superposition theorem.
First we set i2 = 0 and analyse the circuit shown in Fig. 26.
~
i1
R1
R2
v1
~
i2  0
v~2
R3
Fig. 26
As a result we obtain
~
i1 
v1
 f11v1 ,
R1  R3
~
v~2  i1 R3 
R3
v1  f 21v1 ,
R1  R3
f11 
1
,
R1  R3
f 21 
R3
.
R1  R3
(28)
(29)
14
Next we set v1 = 0 and analyse the circuit shown in Fig. 27
~
R1
i1
R2
~
~
v2
R3
i2
Fig. 27
In this circuit we find
~
~
i1  i2
R3
 f12 i2 ,
R3  R1

~
RR 
v~2  i2  R2  1 3   f 22 i2 ,
R1  R3 

f12  
R3
,
R3  R1
f 22  R2 
R1 R3
.
R1  R3
(30)
(31)
To write the state equations we substitute into (27) of f11, f21, f12, f22 given by the formulas
(28)-(31) and iS1  0 , vS 2  0 .