* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Loop and Nodal Analysis and Op Amps
Stray voltage wikipedia , lookup
Ground (electricity) wikipedia , lookup
Power engineering wikipedia , lookup
Mathematics of radio engineering wikipedia , lookup
Electric machine wikipedia , lookup
Topology (electrical circuits) wikipedia , lookup
Electromagnetic compatibility wikipedia , lookup
Wireless power transfer wikipedia , lookup
Resistive opto-isolator wikipedia , lookup
Mains electricity wikipedia , lookup
Three-phase electric power wikipedia , lookup
Current source wikipedia , lookup
Switched-mode power supply wikipedia , lookup
Flexible electronics wikipedia , lookup
Distribution management system wikipedia , lookup
Integrated circuit wikipedia , lookup
History of electric power transmission wikipedia , lookup
Zobel network wikipedia , lookup
Ignition system wikipedia , lookup
Galvanometer wikipedia , lookup
Electrical substation wikipedia , lookup
Earthing system wikipedia , lookup
Loading coil wikipedia , lookup
Opto-isolator wikipedia , lookup
Two-port network wikipedia , lookup
Magnetic core wikipedia , lookup
Alternating current wikipedia , lookup
Transformer wikipedia , lookup
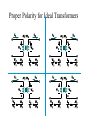
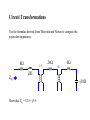
Circuits II EE221 Unit 10 Instructor: Kevin D. Donohue Magnetically Coupled Circuits, Linear Transformers, Transformer Circuits Coupling Coefficient The coupling coefficient is a measure of the percentage of flux from one coil that links another (mutual inductance) coil. The coupling coefficient for 2 mutual inductors is given by: k M L2 L1 If k > 0.5 , then most of the flux from the one coil links the other and the coils are said to be tightly coupled. If k < 0.5, then most of the flux is not shared between the 2 coils and in this case the coils are said to be loosely coupled. Linear Transformers A transformer is a 4-terminal device comprised of 2 or more magnetically coupled coils. In a typical application they are used the change the ratio of current to voltage (maintaining constant power) from a source to a load. R1 R2 + ZL Vs - Primary Coil Secondary Coil Linear Transformers Equivalent (T Network) A z parameter model of a T (or Y) network of inductors is given by: La i1 + Lb i2 + Lc v1 v2 - v1 z11 v z 2 21 Vˆ1 j ( La Lc ) ˆ jLc V2 z12 i1 z22 i2 jLc Iˆ1 j ( Lb Lc ) Iˆ2 Find the equivalent T network for a transform circuit given by a mutual inductance pair. Show equivalent T network requires: M I1 + V1 - + L1 L2 V2 - I2 Lc M La L1 M Lb L2 M Linear Transformers Equivalent (T Network) By setting the corresponding y-parameter model elements equal, the transformer can be mapped to the following equivalent T network. L1-M i1 + v1 M - i2 L2-M + v2 - y-parameter equivalent model for transformer is given by: L2 Iˆ1 j ( L1 L2 M 2 ) ˆ M I 2 j ( L1 L2 M 2 ) M j ( L1 L2 M 2 ) Vˆ1 L1 Vˆ2 j ( L1 L2 M 2 ) A similar equivalence can be obtained for the or network. Ideal Transformers For ideal transformers assume that coupling coefficient is 1. If this is the case, then both coils have the same flux. Assume the polarities of the voltages and currents result in flux going in the same direction. Then the result is: v1 N1 d dt and v2 N 2 d dt Vˆ2 N 2 n Vˆ1 N1 And for the ideal transformer assume no power is lost in the magnetic circuit (infinite permeability) or the coils (no wire resistance), which implies: Vˆ1 Iˆ1* Vˆ2 Iˆ2* Iˆ1 Vˆ2 N 2 n ˆI ˆ V1 N1 2 Proper Polarity for Ideal Transformers Example Find Vˆo with Z1 = 10, Z2 = -j50, and ZL=20 Z1 Z2 1:4 + + 1200 - ZL Vo - Circuit Transformations The primary circuit can be transformed into the secondary by performing a Thévenin equivalent at the terminals of the transformer secondary. Z1 Z2 1:n + + Vs2 Vs1 - - Primary Coil Secondary Coil Circuit Transformations The result is: n2Z1 + nVs1 - Z2 + Vs2 - Example Find Vˆo with Z1 = 10, Z2 = -j50, and ZL=20 Z1 Z2 1:4 + + 1200 - ZL Vo - Circuit Transformations The result is: Z1 + Vs1 - Z2 / n2 + Vs2 / n - Circuit Transformations Perform a Norton transformation on the above circuits to show how a current source transforms to an equivalent on the primary or secondary circuits. In summary: Reflecting the secondary circuit to the primary side requires impedance division by n2, voltage source division by n, and current source multiplication by n. Reflecting the primary circuit to the secondary side requires impedance multiplication by n2, voltage source multiplication by n, and current source division by n. Circuit Transformations Use the formulae derived from Thévenin and Norton to compute the equivalent impedance. 8 Zeq 1:5 24 4:1 6 j2 Show that Zeq = 12.8 + j5.6 -j10