* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Quantum Transition
Atomic theory wikipedia , lookup
Topological quantum field theory wikipedia , lookup
Dirac bracket wikipedia , lookup
Hidden variable theory wikipedia , lookup
Renormalization group wikipedia , lookup
Density matrix wikipedia , lookup
Ising model wikipedia , lookup
Particle in a box wikipedia , lookup
X-ray fluorescence wikipedia , lookup
Schrödinger equation wikipedia , lookup
Franck–Condon principle wikipedia , lookup
History of quantum field theory wikipedia , lookup
Renormalization wikipedia , lookup
Density functional theory wikipedia , lookup
X-ray photoelectron spectroscopy wikipedia , lookup
Path integral formulation wikipedia , lookup
Canonical quantization wikipedia , lookup
Electron configuration wikipedia , lookup
Theoretical and experimental justification for the Schrödinger equation wikipedia , lookup
Dirac equation wikipedia , lookup
Hydrogen atom wikipedia , lookup
Scalar field theory wikipedia , lookup
Tight binding wikipedia , lookup
Relativistic quantum mechanics wikipedia , lookup
Probability amplitude wikipedia , lookup
Molecular Hamiltonian wikipedia , lookup
Cross section (physics) wikipedia , lookup
Perturbation theory wikipedia , lookup
Quantum Transition
* Time-Dependent Perturbation Theory
* Fermi-Golden Rule
*Impurity Scattering
Time Evolution of Quantum States
In quantum mechanics, one in general deals with two kinds of problems. One is to
determine all possible states of a system. This is possible only if the Hamiltonian of
the system is time independent, that is, the potentials or forces do not vary from
time to time. The basic procedure is to solve time-independent Schrödinger
equation with all kinds of approximations, as what we have already seen.
When the Hamiltonian is time dependent, the state or the wavefunction
of the system will be also time dependent. In other words, an electron will have a
probability to transfer from one state (molecular orbital) to another. The
transition probability can be obtained from the time-dependent Schrödinger Eq.
∂Ψ (t ) ⌢
iℏ
= HΨ ( t )
∂t
(23.1)
Equation 1 says once the initial wavefunction, Ψ(0), is known, the wavefunction at a
given later time can be determined. If H is time independent, we can easily found that
Ψ (t ) = ∑ a n e − iEnt / ℏψ n
(23.2)
n
2
In this case, it is easy to see that Ψ (t ) = Ψ (0)
so the probability density does not change.
2
(23.3)
Time Evolution of Quantum States
If a system has initial (t=0) Hamiltonian, H0 (time independent), and is at an initial
eigenstate, ψk. Under an external influence, described by H’ (time dependent), the
system will change state. For example, a molecule moves close to an electrode
surface to feel an increasing interaction with the electrode. The combined
Hamiltonian is
Hˆ (t ) = Hˆ 0 (0) + Hˆ ' (t )
(23.4)
The wavefunction of the system corresponding to the combined Hamiltonian should
be a linear combination of the initial eigenstates,
Ψ (t ) = ∑ C nk (t )ψ n
(23.5)
n
From mathematical point of view, this is always possible since the initial eigenstates,
ψn, form a complete set of basis. The physical picture is that the system under the
influence of the external perturbation will end up in a different state with a
probability given by |Cnk|2. The indices nk mean a transition from kth eigenstate to
nth eigenstate. How fast the transition is or the transition rate is given by
d
wnk = |C nk (t ) |2
dt
(23.6)
Time-Dependent Perturbation Theory
Now we determine the transition rate according to the above definition. We assume
that the initial state of the system is
Ψ ( 0) = ψ k
(23.7)
the external perturbation, H’, is switched on at t=0. The time dependent Schrödinger
Eq. is
⌢
⌢
∂Ψ(t )
iℏ
= ( H 0 + H ' )Ψ(t )
∂t
(23.8)
For simplicity, we can rewrite Eq. 23.5 as
Ψ (t ) = ∑ Cnk '(t )e − iEnt / ℏψ n
(23.9)
n
Note that Cnk’(t) in Eq. 23.9 is different from Cnk(t) that in Eq. 23.5, but
|Cnk’(t)|2=| Cnk(t)|2 and we can omit the prime in equation 10. Substituting Eq. 23.9
into Eq. 23.8, we have (can you show it?)
⌢
dCnk −iEnt / ℏ
− iEn t / ℏ
iℏ ∑
e
ψ n = ∑ Cnk e
Hψ
' n.
dt
n
n
(23.10)
Time-Dependent Perturbation Theory
Multiplying Eq. 23.10 by ψk’ and integrate, we obtain
⌢
dCk 'k
−i ( Ek ' − En ) t / ℏ
iℏ
= ∑e
< k ' | H ' | n >C nk
dt
n
(23.10)
After considering that ψn are normalized orthogonal functions. Note that the initial
condition, Eq. 23.7, becomes
Cnk (0) = δ nk
(23.11)
In general, solving Eq. 23.10 with initial condition 14 is not easy, but we can obtain
approximate solution using perturbation theory when H’ is small comparing to H0.
Let us denote the solution in the absence of H’ as Cnk(0), we have
dC k 'k
iℏ
dt
(0)
=0
(23.12)
So Ck’k(0) is independent of time and the initial condition is
Ckk ' (0) = δ kk '
Cnk (0) = δ nk
Time-Dependent Perturbation Theory
We replace Cnk on the right hand side of Eq. 23.10 with Cnk(0) and obtain the first
order correction
dC
iℏ k 'k
dt
(1)
⌢
= e − i ( Ek ' − Ek ) t / ℏ < k ' | H ' | k >
(23.13)
⌢
< k ' | H ' | k > in the above equation is often denoted as H’k’k and it measured the
coupling strength between the k’ and k states. Solving Eq. 23.13, we have
t
C k 'k
1
= ∫ H k' 'k e −i ( Ek ' − Ek ) t / ℏ dt,
iℏ 0
(23.14)
One important case is that H’ is fixed once switched on. In this case, Eq. 23.14
becomes
1 ' e − i ( E k ' − Ek ) t / ℏ − 1
C k 'k ( t ) = H k 'k
iℏ
i( Ek ' − Ek ) / ℏ
(23.15)
Fermi-Golden Rule
From Eq. 23.15, we can obtain
2
1
2πt
t →∞
'
2 sin (( E k ' − E k )t / ℏ )
| C k 'k ( t ) | = 2 | H k 'k |
→
| H k' 'k |2 δ ( E k ' − E k )
2
2
ℏ
[( E k ' − E k ) / ℏ ]
ℏ
2
(23.16)
So the transition rate is
wk 'k
2π
= 2 | H k' 'k |2 δ ( E k ' − E k )
ℏ
(23.17)
We can conclude from Eq. 23.17 that (1) the transition rate is independent of time,
(2) the transition can occur only if the final state has the same energy as the
initial state. The later one reflects energy conservation. In the case when the
energy levels are continuous band, the number of states near Ek’ for an interval of
dEk’ is In the case when the energy levels are continuous band, the number of
states near Ek’ for an interval of dEk’ is ρ(Ek’)dEk’ , where ρ is the density of states.
The transition rate from k state to the states near Ek’ is then
w = ∫ ρ ( E k ' ) wk 'k dE k ' =
This is Fermi Golden rule,
2π
'
2
|
H
|
ρ ( Ek )
k
'
k
ℏ2
(23.18)
Time dependent perturbation theory - Revisited
• Assume the Hamiltonian may be decomposed as H=H0+Vs,
where H0 is the Hamiltonian of the perfect crystal (described by
Bloch states), Vs(r,t) is a small random potential. If Vs<<H0, then
it is a good approximation to expand the solution (with random
part) in terms of unperturbed eigenstates:
H 0ψ k = E k ψ k ;
ψ 0k (r, t ) = ψ k (r )e − iE t / ℏ
k
• Expand actual solution in terms of these orthonormal functions:
ψ (r, t ) = ∑ c k (t )ψ k (r )e − iE t / ℏ
k
k
• If the initial wave packet is centered around ko, so that
ck (t ) ≈ 1
ck ≠ k (t ) ≈ 0
0
0
• In the limit at t→∞, the probability of finding the particle in
another state ko′ is
Pk k ′ = lim ck ′ (t )
0
0
t → ∞
2
k ′0
k0
0
Vs
• Define the transition rate
Γk k ′ = lim
0
• Solve for
0
c k ′ (t )
t → ∞
2
0
t
ck 0′ using the S.E. and the previous expansion
{H 0 + Vs }∑ ck (t )ψ k (r )e
k
− iE k t / ℏ
∂
= iℏ ∑ ck (t )ψ k (r )e − iE t / ℏ
∂t k
k
H0 part cancels with phase factor on RHS
Vs ∑ ck (t )ψ k (r )e
− iE k t / ℏ
k
∂ck (t )
ψ k (r )e −iE t / ℏ
= iℏ ∑
∂t
k
• Multiply both sides by ψ k ′ (r )e
k
− iE k 0′ t / ℏ
0
iℏ
∂c k ′ (t )
0
∂t
and integrate
= ∑ c k (t ) k 0′ Vs k e
− i (E k 0′ − E k )t / ℏ
k
where the matrix element, using Dirac notation, is defined as
k 0′ Vs k = ∫ drψ k* ′Vs (r, t )ψ k ′
0
• Assume sufficiently weak scattering that cko≈1, and ck≠≠ko≈0 for
all time. The dominant term in the sum is:
iℏ
∂ck ′ (t )
0
∂t
= ck (t ) k 0′ Vs k 0 e
− i (E k 0′ − E k 0 )t / ℏ
0
which integrates to
1t
− i (E
ck ′ (t ) = ∫ dt ′ k 0′ Vs k 0 e
iℏ 0
0
k 0′
− E k 0 )t ′ / ℏ
+ ck ′ (0 )
0
• Suppose V(r,t) may be Fourier decomposed, so that
Vs (r, t ) = Vs (r )e ∓ iωt
Note that this form of V(r,t) may correspond to interaction with
lattice vibrations or with optical excitation.
• Then substituting
t
1
c k ′ (t ) =
k 0′ Vs k 0 ∫ dt ′e − iΛt ′ ; Λ = (E k ′ − E k ∓ ℏω) / ℏ
iℏ
0
0
0
and integrating this last expression leads to
1 k k ′ e − iΛ t − 1
ck ′ (t ) = V s
iℏ
iΛ
1 k k ′ − iΛt / 2 sin(Λt )
c k ′ (t ) = Vs e
t
iℏ
Λt
0
0
0
0
0
0
• Since the probability of being in k0′ is given by
Pk k ′ = lim ck ′ (t )
0
0
t → ∞
0
2
0
• Substituting for c and taking the magnitude squared gives
1 k k ′ 2 sin(Λt ) 2
= lim 2 Vs
t
t → ∞ ℏ
Λt
2
Pk k ′
0
0
0
0
where asymptotically
sin(Λt )
lim
= 2πδ(Λ ) / t = 2πℏδ(E k ′ − Ek ∓ ℏω) / t
t → ∞
Λt
2
0
0
This gives the famous Fermi’s Golden Rule (droping 0s index)
Γkk ′
Pkk ′ 2 π kk ′ 2
=
=
Vs
δ(E k ′ − E k ∓ ℏω)
t
ℏ
• Assumptions made:
(1) Long time between scattering (no multiple scattering events)
(2) Neglect contribution of other c’s (Collision broadening ignored)
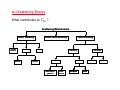
A.3 Scattering Theory
What contributes to Γkk′ ?
Scattering Mechanisms
Defect Scattering
Crystal
Defects
Neutral
Impurity
Carrier-Carrier Scattering
Alloy
Ionized
Lattice Scattering
Intervalley
Intravalley
Acoustic
Deformation
potential
Optical
Piezoelectric
Nonpolar
Acoustic
Polar
Optical
Ionized Impurities Scattering
(Ionized donors/acceptors, substitutional impurities, charged
surface states, etc.)
• The potential due to a single ionized impurity with net charge
Ze is:
2
Ze
Vi (r ) = −
4πεr
0
mks units
• In the one electron picture, the actual potential seen by
electrons is screened by the other electrons in the system.
What is Screening?
λD - Debye screening length
-
+
r
3D:
-
1
r
screening
cloud
r
1
exp −
r
λD
-
-
Example:
-
-
-
-
Ways of treating screening:
• Thomas-Fermi Method
static potentials + slowly varying in space
• Mean-Field Approximation (Random Phase Approximation)
time-dependent and not slowly varying in space
• Considering the induced charge caused by the change in the
electron gas by the impurity, the net potential seen is
V 0 i (q )
Vi (q ) =
ε(q, ω)
In the above expression, q is the wavevector associated with
Fourier transforming the potential (and Poisson’s equation),
Vi(q) is the total potential seen by an electron due to an
impurity, and ε(q,ω) is the dielectric function characterizing the
polarization of the electron gas to the impurity potential.
• In linear response theory, this may be calculated in the random
phase approximation (RPA) to give the Lindhard dielectric
function
f0 (E k + q ) − f0 (E k )
e2
ε(q, ω) = 1 − lim
∑
s →∞ ε q 2 k E
k + q − E k + ℏω + iδ
sc
• Assuming low frequencies, and assuming long wavelengths, the
Thomas-Fermi function is obtained to be of the form:
λ2
lim ε(q, ω) ≈ 1 + 2
ω,q → 0
q
where the inverse screening length λ2 is given as (3D):
2
e
n
2
λ =
εsc kBT
2
3
e
n
2
high temperatur e; λ =
; T = 0K
2εsc EF
In here, n is the carrier density and EF is the Fermi energy.
• Assuming the Fermi Thomas form, inverse Fourier transforming
gives the form of the screened potential in real space as:
Zq 2 − λr
Vi (r ) = −
e
4πεr
• For the scattering rate due to impurities, we need for Fermi’s
rule the matrix element between initial and final Bloch states
n′, k′ Vi (r ) n, k = V −1 ∫ drun* ′,k ′e −ik′⋅rVi (r )un,k e ik⋅r
Since the u’s have periodicity of lattice, expand in reciprical
space
= ∑ V −1 ∫ dre − ik′⋅rVi (r )e ik ⋅r e − iG ⋅rU nn′kk ′ (G )
G
= ∑ V −1 ∫ dre − ik′⋅rVi (r )e ik ⋅r e −iG ⋅r ∫ dr′un* ′,k ′ (r′)un,k (r′)e iG ⋅r′
Ω
G
• For impurity scattering, the matrix element has a 1/q type
dependence which usually means G≠0 terms are small
= V −1 ∫ dre − ik′⋅rVi (r )e ik ⋅r ∫ dr′un* ′,k ′ (r′)un,k (r′) = Vi (q )Ikk ′
Ω
nn ′
• The usual argument is that since the u’s are normalized within a
unit cell (i.e. equal to 1), the Bloch overlap integral I, is
approximately 1 for n′=n [interband(valley)]. Therefore, for
impurity scattering, the matrix element for scattering is
approximately
k′ Vi (r ) k
2
= Vi (q )
2
Z 2e 4
≅ 2 2
; V = volume
2 2
V q + λ εsc
(
)
where the scattered wavevector is: q = k − k ′
• This is the scattering rate for a single impurity. If we assume that
there are Ni impurities in the whole crystal, and that scattering is
completely uncorrelated between impurities:
Vi
kk ′
N i Z 2e 4
ni Z 2 e 4
≅ 2 2
=
2 2
2
V q + λ εsc V q 2 + λ2 εsc
(
)
(
)
where ni is the impurity density (per unit volume).
• The total scattering rate from k to k′ is given from Fermi’s golden
rule as:
Γki k ′
2πni Z 2e 4
=
δ(E k′ − E k )
2
2 2
Vℏ q + λ εsc
(
)
If θ is the angle between k and k′, then:
q = k − k ′ = k 2 + k ′2 − 2kk ′ cos θ = 2k 2 (1 − cos θ )
• Comments on the behavior of this scattering mechanism:
- Increases linearly with impurity concentration
- Decreases with increasing energy (k2), favors lower T
- Favors small angle scattering
- Ionized Impurity-Dominates at low temperature, or room
temperature in impure samples (highly doped regions)
• Integration over all k′ gives the total scattering rate Γk :
2 4
2
*
4
n
Z
e
m
k
Γki = i 2 3 3 2
8πεsc ℏ k qD 4k 2 + qD2
(
; qD = 1 / λ
)
Total Electron Scattering Rate Versus Energy:
Intrinsic Si
GaAs
In both cases the electron scattering rates were calculated
by assuming non-parabolic energy bands.