Download Computational Geometry of Molecular Structure

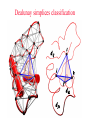
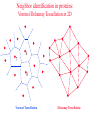
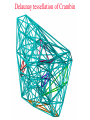
CASB workshop, 9/23/10
Protein Function Analysis using
Computational Mutagenesis
Iosif Vaisman
Laboratory for Structural Bioinformatics
proteins.gmu.edu
Department of Bioinformatics and
Computational Biology
Dealunay simplices classification
Protein representation (Crambin)
Neighbor identification in proteins:
Voronoi/Delaunay Tessellation in 2D
Delaunay simplex is
defined by points,
whose Voronoi
polyhedra have
common vertex
Delaunay simplex is
always a triangle in
a 2D space and a
tetrahedron in a 3D
space
Voronoi Tessellation
Delaunay Tessellation
Neighbor identification in proteins:
Voronoi/Delaunay Tessellation in 2D
6
7
6
Voronoi Tessellation
Delaunay Tessellation
Delaunay tessellation of Crambin
Delaunay Tessellation of Protein Structure
D (Asp)
Cα or center of mass
Abstract each amino acid to a point
Atomic coordinates – Protein Data Bank (PDB)
A22
L6
D3
F7
G62
K4
S64
R5
C63
Delaunay tessellation: 3D “tiling” of space into non-overlapping,
irregular tetrahedral simplices. Each simplex objectively defines a
quadruplet of nearest-neighbor amino acids at its vertices.
Compositional propensities of Delaunay simplices
k
q ijkl
l
i
j
fijkl
 log
pijkl
f- observed quadruplet frequency,
pijkl = Caiajakal, a - residue frequency
AAAA: C = 4! / 4! = 1
AAAV: C = 4! / (3! x 1!) = 4
AAVV: C = 4! / (2! x 2!) = 6
AAVR: C = 4! / (2! x 1! x 1!) = 12
AVRS: C = 4! / (1! x 1! x 1! x 1!) ) = 24
C
4!
n
 (t !)
i
i
Counting Quadruplets
•
assuming order independence among residues comprising
Delaunay simplices, the maximum number of all possible
combinations of quadruplets forming such simplices is 8855
C D E F
 20 
 
 4
4845
C C D E
 19 
20   
2
3420
C C D D
 20 
 
 2
190
C C C D
20 19
380
C C C C
20
20
8855
Log-likelihood of amino acid quadruplets
with different compositions
Log-likelyhood ratio
1.5
1.0
0.5
0.0
-0.5
-1.0
-1.5
1
2
3
4
5
6
7
8
9
...
CCCC
CCCY
CCHH
CCCG
CCCH
CCCW
CCCS
CCCQ
CCCF
...
2000
3.081003
2.13004
1.960814
1.782267
1.742759
1.724275
1.724275
1.657329
1.621613
...
8000
6000
4000
...
8343
8344
8345
8346
8347
8348
8349
8350
8351
...
CDDL
IRRV
AEYY
KKRV
CKRS
CEKP
HKKS
CGLR
ACKN
...
-0.90166
-0.90217
-0.90535
-0.95081
-0.96133
-0.98433
-0.98472
-1.14737
-1.16297
Delaunay simplices with distinct composition
Log-likelihood of amino acid quadruplets
Log-likelihood of amino acid quadruplets
Computational Mutagenesis Methodology
• Observations:
• Relatively few mutant and wt structures of same protein have been solved
• Tessellations of mutant and wt protein structures are very similar or identical
• Approach:
• Obtain topological score (TSmut) and 3D-1D potential profile vector (Qmut)
for any mutant protein by using the wt structure tessellation as a template
• Simply change the residue label at a given point(s) and re-compute
s(R,D,A,L)
A22
s(I,D,A,L)
L6 s(R,G,F,L) Mutation
F7
D3
(R5  I5)
s(R,D,K,S)
G62
K4
S64
R5
A22
L6 s(I,G,F,L)
D3
F7
s(I,D,K,S)
G62
K4
S64
s(R,S,C,G)
C63
(TSwt, Qwt)
I5
s(I,S,C,G)
C63
(TSmut, Qmut)
Computational Mutagenesis Methodology
• Scalar “Residual Score” of a mutant:
(mutant – wt) topological score difference = TSmut – TSwt (empirical
measure of relative structural change due to mutation)
• Vector “Residual Profile” of a mutant:
R = Qmut – Qwt = (mutant – wt) 3D-1D potential profile difference
(environmental perturbation score at every position in structure)
• Denote R = < EC1, EC2, EC3,…, ECN >
ECi = qi,mut – qi,wt = relative Environmental Change at position i
• Geometric property: If mutant is due to a single substitution at
position j, then ECj ≡ mutant residual score (“epicenter” of impact)
• The only other nonzero EC components correspond to neighboring
positions that participate in simplices with j
Approach 1: Protein Topological Score (TS)
• Obtained by summing the log-likelihood scores of all simplicial
quadruplets defined by the protein tessellation
• Global measure of protein sequence-structure compatibility
• Total (empirical or statistical) potential of the protein
TS = ∑î s(î), sum taken over all simplex
quadruplets î in the entire tessellation.
s(R,D,A,L)
A22
L6 s(R,G,F,L)
D3
F7
s(R,D,K,S)
G62
K4
S64
R5
s(R,S,C,G)
C63
Close-up view of only the four simplices that
use R at position 5 as a vertex (hypothetical)
Approach 2: Residue Environment Scores
• For each amino acid position, locally sum the log-likelihood scores
s(i,j,k,l) of only simplex quadruplets that include it as a vertex
s(R,D,A,L)
A22
L6 s(R,G,F,L)
D3
F7
s(R,D,K,S)
G62
K4
S64
R5
Example: q5 = q(R5) = ∑(i,j,k,l) s(i,j,k,l),
sum over all simplex quadruplets
(i,j,k,l) that include amino acid R5
s(R,S,C,G)
C63
• The scores of all amino acid positions in the protein structure
form a 3D-1D Potential Profile vector Q = < q1, q2, q3,…,qN >
(N = length of primary sequence in solved structure)
Reversibility Analysis
S1,E1
‘reference’ PDB
S1,E2
Calculated Mutant
Forward Mutation
S2,E2
Mutant PDB
S2,E1
Calculated ‘reference’
Reverse Mutation
Reversibility of mutations (T4 lysozyme)
Protein
Mutation
1l63
180l
T26E
E26T
1l63
123l
1l63
1cu3
A82S
S82A
V87M
M87V
Score change
-2.49
2.01
4
3
1.49
-1.49
2
1
-0.28
0.22
0
-4
1l63
138l
A93C
C93A
-1.98
1.78
-3
-2
-1
0
1
2
-1
-2
R2 = 0.9886
1l63
1goj
T152S
S152T
-1.08
1.12
-3
3
Reversibility
Analysis
Reversibility Analysis
Reverse mutation potential score difference
15
y = -0.9918x - 0.0251
R2 = 0.9742
10
5
0
(4pnp,1ao9)
-5
-10
-15
-15
-10
-5
0
5
Forw ard m utation potential score difference
10
15
Functional Effects of Amino Acid Substitutions
• Change in protein stability:
• Effect on melting temperature: ΔTm = Tm (mutant) – Tm (wt)
• Effect on thermal denaturation: ΔΔG = ΔG (mutant) – ΔG (wt)
• Effect on denaturant denaturation: ΔΔGH2O = ΔGH2O (mutant) – ΔGH2O (wt)
• Change in protein activity:
• Mutant enzymatic activity relative to wt
• Mutant strength of DNA binding relative to wt
• Disease potential of human coding nsSNPs
• Neutral polymorphism or disease-associated mutation?
• For protein targets of inhibitor drugs:
• Continued susceptibility or (degree of ) resistance that patients with the
mutant protein have to the inhibitor
• Inhibitor binding energy to mutant target relative to wt
Examples ofExperimental Mutagenesis Data
•
HIV-1 protease (99 aa’s): 536 single point
mutants (at least one at each position)
–
•
Bacteriophage T4 lysozyme (164 aa’s):
2015 single point mutants (12-13 at each
position except first)
–
•
D. D. Loeb et al., Nature 340, 397
(1989).
D. Rennell et al., J. Mol. Biol. 222, 67
(1991).
E. coli lac repressor (360 aa’s): 4041
single point mutants (12-13 at positions 2
to 329)
–
P. Markiewicz et al., J. Mol. Biol. 240,
421 (1994).
Example: HIV-1 Protease (PR)
HIV-1 PR Dataset Example:
Residual Profiles of 536 Experimental Mutants
…
…
Experimental Mutants: Residual Scores
Elucidate the Structure-Function Relationship
536 HIV-1 protease mutants
630 hIL-3 mutants
4041 lac repressor mutants
371 gene V protein mutants
Universal Model Approach:
8635 Experimental Mutants from 7 Proteins
Universal Model Approach:
980 Experimental Mutants from 20 Proteins
Mean Residual Score _
0.6
0.3
0
-0.3
-0.6
-0.9
Increased
Decreased
Mutant Protein Stability Change
Structure-Function Correlation Based on
Residual Scores: nsSNPs
• 1790 nsSNPs corresponding to single amino acid substitutions
in several hundred proteins with tessellatable structures
• Function: 1332 nsSNPs associated with disease; 458 neutral
• Data obtained from Swiss-Prot and HPI
Structure-Function Correlation Based on
Residual Scores: Drug Susceptibility
Mean Residual Score_
0.00
-0.20
-0.40
NFV: -0.26
SQV: -0.19
IDV: -0.48
RTV: 0.09
APV: -0.49
LPV: -0.41
ATV: 0.05
Average: -0.28
-0.60
-0.80
NFV: -0.18
SQV: -1.05
IDV: -0.93
RTV: -0.87
APV: -0.80
LPV: -0.78
ATV: -0.72
Average: -0.77
-1.00
NFV: -1.10
SQV: -1.23
IDV: -1.00
RTV: -0.99
APV: -1.24
LPV: -1.04
ATV: -1.17
Average: -1.09
-1.20
Sensitive
Intermediate
Resistant
Susceptibility to HIV-1 Protease Inhibitors
Algorithm Performance: 2015 T4 Lysozyme Mutants
Learning Curves for HIV-1 protease and
T4 lysozyme mutants
Real-World Application: T4 Lysozyme Predictions
• Experimental data (not part of training set) obtained from ProTherm database
• Result: predictions match experiments for 30/35 (~86%) of the mutants
T4 Lysozyme Mutational Array
Training set mutants (n = 2015)
Active
Inactive
Predicted test set mutants (n = 1101)
Active
Inactive
GVP Mutational Array
Support Vector Regression
Capriotti et al. SVM regression (for comparison):
r = 0.71, Standard Error = 1.3 kcal/mol, y = 0.5223x – 0.4705
Conclusions
• Computational mutagenesis derived from a four-body,
knowledge-based statistical potential uniquely
characterizes each protein mutant using both sequential
and structural features
• Attributes correlate well with mutant function valuable for developing accurate machine learning
based predictive models
Acknowledgements
Structural Bioinformatics Laboratory (GMU):
Collaborators:
Tariq Alsheddi
David Bostick
Andrew Carr
Sunita Kumari
Yong Luo
Majid Masso
John Grefenstette (GMU)
Curt Jamison (GMU)
Dmitri Klimov (GMU)
Dan Carr (GMU)
Estela Blaisten (GMU)
Vladimir Karginov (IB)
Ewy Mathe
Olivia Peters
Vadim Ravich
Greg Reck
Todd Taylor
Bill Zhang
(structure alignment)
(topological similarity)
(functional sites, visualization)
(structural genomics)
(evolutionary structure analysis)
(mutagenesis, HIV-1 protease,
LAC repressor, T4 lysozyme, SNP)
(mutagenesis, p53)
(protein-protein interfaces)
(HIV RT mutagenesis)
(hydration potentials, amyloids)
(statistical potentials, secondary
structure, topology, protein stability)
(mutagenesis, BRCA1)
Unpublished data:
Clyde Hutchison (UNC)
Ron Swanstrom (UNC)
Funding:
NSF
NIH-Innovative Biologics
GMU-INOVA Research
Fund
Evaluating Algorithm Performance
• Overall goal: Develop model with known examples to accurately
predict class (or value) of instances that have not yet been assayed
experimentally (potentially great savings of time and money)
• Ideal situation: split large original dataset into 3 subsets
o
o
o
o
Training set (learn model)
Validation set (optimize model by tweaking model parameters)
Test set (evaluate model on new data not used to develop model)
Errors measured at each step (resubstitution, validation, generalization)
• Approaches: Tenfold cross-validation (10-fold CV);
leave-one-out CV (i.e., jackknife or N-fold CV, N = dataset size);
% split (e.g., use only 2/3 for training, 1/3 held out for testing)
Evaluating Algorithm Performance
• 10-fold CV
o Randomly split the dataset instances into 10 equally-sized subsets
o Hold-out subset 1; combine subsets 2-10 into one training set for learning a
model; use trained model to predict classes of instances in subset 1
o Repeat previous step 9 more times (e.g., hold-out subset 2, combine subsets
1 and 3-10 together to train a model, use model to predict subset 2, etc)
o We end up with 10 models, each trained using 90% of the original dataset,
and each used to predict the held-out 10% subset.
o In the end, each instance has one class prediction – compare to actual class
•
LOOCV (leave-one-out CV, jackknife, or N-fold CV)
o Similar to above, but each subset contains only 1 instance
o Deterministic – no randomness to which instances are grouped as subsets
o Overall prediction accuracy provides rough idea of how a model trained
with the full dataset will perform
• % split (self-explanatory)
Evaluating Algorithm Performance
• Assume instances belong to two generic classes (Pos/Neg)
• Results of comparing predictions with actual classes based on
the approaches described (10-fold CV, LOOCV, % split) can be
summarized in a confusion matrix:
Predicted as
Actual
class
Pos
Neg
Pos
TP
FN
Neg
FP
TN
• Classification performance measures:
accuracy = (TP+TN) / (TP+FP+TN+FN); sensitivity = TP / (TP+FN);
specificity = TN / (TN+FP); precision = TP / (TP+FP);
BER = 0.5 × [FP / (FP+TN) + FN / (FN+TP)];
MCC = (TP×TN – FP×FN) / (TP+FN)(TP+FP)(TN+FN)(TN+FP);
AUC = area under ROC curve (plot of sensitivity vs. 1 – specificity)
• For regression models: correlation coefficient, standard error
ROC Curve
• Plot of true positive rate (sensitivity) versus false positive rate
(1 – specificity) in the unit square
• AUC = probability that classifier will rank a randomly chosen
positive instance higher than a randomly chosen negative one
• AUC ~ 0.5 (ROC close to diagonal line joining points (0,0) and
(1,1)) suggests no signal in dataset and that trained model is not
likely to perform any better than random guessing
• AUC = 1 (piecewise linear ROC joining (0,0) to (0,1) and (0,1)
to (1,1)) indicates a perfect classifier