Download F10 - IDt

CD5560
FABER
Formal Languages, Automata
and Models of Computation
Lecture 13
Mälardalen University
2010
1
Content
Alan Turing and Hilbert Program
Universal Turing Machine
Chomsky Hierarchy
Decidability
Reducibility
Uncomputable Functions
Rice’s Theorem
Interactive Computing, Persistent TM’s (Dina Goldin)
2
http://www.turing.org.uk/turing/
Who was Alan Turing?
Founder of computer science,
mathematician,
philosopher,
codebreaker,
visionary man before his time.
http://www.cs.usfca.edu/www.AlanTuring.net/turing_archive/index.html- Jack
Copeland and Diane Proudfoot
http://www.turing.org.uk/turing/ The Alan Turing Home Page
Andrew Hodges
3
Alan Turing
1912 (23 June): Birth, London
1926-31: Sherborne School
1930: Death of friend Christopher Morcom
1931-34: Undergraduate at King's College, Cambridge University
1932-35: Quantum mechanics, probability, logic
1935: Elected fellow of King's College, Cambridge
1936: The Turing machine, computability, universal machine
1936-38: Princeton University. Ph.D. Logic, algebra, number theory
1938-39: Return to Cambridge. Introduced to German Enigma cipher machine
1939-40: The Bombe, machine for Enigma decryption
1939-42: Breaking of U-boat Enigma, saving battle of the Atlantic
4
Alan Turing
1943-45: Chief Anglo-American crypto consultant. Electronic work.
1945: National Physical Laboratory, London
1946: Computer and software design leading the world.
1947-48: Programming, neural nets, and artificial intelligence
1948: Manchester University
1949: First serious mathematical use of a computer
1950: The Turing Test for machine intelligence
1951: Elected FRS. Non-linear theory of biological growth
1952: Arrested as a homosexual, loss of security clearance
1953-54: Unfinished work in biology and physics
1954 (7 June): Death (suicide) by cyanide poisoning, Wilmslow, Cheshire.
5
Hilbert’s Program, 1900
Hilbert’s hope was that mathematics would be reducible to
finding proofs (manipulating the strings of symbols) from a
fixed system of axioms, axioms that everyone could agree
were true.
Can all of mathematics be made algorithmic, or will there
always be new problems that outstrip any given algorithm,
and so require creative acts of mind to solve?
6
TURING MACHINES
7
Turing’s "Machines". These machines are humans who calculate.
(Wittgenstein)
A man provided with paper, pencil, and rubber, and subject to strict
discipline, is in effect a universal machine.
(Turing)
8
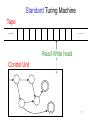
Standard Turing Machine
Tape
......
......
Read-Write head
Control Unit
9
The Tape
No boundaries -- infinite length
......
......
Read-Write head
The head moves Left or Right
10
......
......
Read-Write head
The head at each time step:
1. Reads a symbol
2. Writes a symbol
3. Moves Left or Right
11
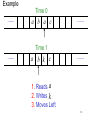
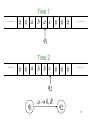
Example
......
Time 0
a b a c
......
Time 1
......
a b k c
......
1. Reads a
2. Writes k
3. Moves Left
12
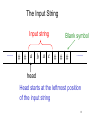
The Input String
Input string
......
Blank symbol
# # a b a c # # #
......
head
Head starts at the leftmost position
of the input string
13
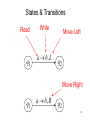
States & Transitions
Read
q1
Write
a  b, L
Move Left
q2
Move Right
q1
a  b, R
q2
14
Time 1
......
# # a b a c # # #
......
q1
Time 2
......
# # a b b c # # #
......
q2
q1
a  b, R
q2
15
Determinism
Turing Machines are deterministic
Not Allowed
Allowed
a  b, R
q2
a  b, R
q2
a  d, L
q3
q1
q1
b  d, L
q3
No lambda transitions allowed in standard TM!
16
Formal Definitions
for
Turing Machines
17
Transition Function
q1
a  b, R
q2
 (q1, a)  (q2 , b, R)
18
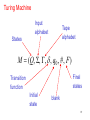
Turing Machine
Input
alphabet
Tape
alphabet
States
M  (Q, , ,  , q0 , # , F )
Final
states
Transition
function
Initial
state
blank
19
Universal Turing Machine
20
A limitation of Turing Machines:
Turing Machines are “hardwired”
they execute
only one program
Better are reprogrammable machines.
21
Solution: Universal Turing Machine
Characteristics:
• Reprogrammable machine
• Simulates any other Turing Machine
22
Universal Turing Machine
simulates any other Turing Machine
M
Input of Universal Turing Machine
• Description of transitions of M
• Initial tape contents of
M
23
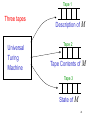
Tape 1
Three tapes
Universal
Turing
Machine
Description of M
Tape 2
Tape Contents of
M
Tape 3
State of
M
24
Tape 1
Description of
M
We describe Turing machine
as a string of symbols:
We encode
M
M as a string of symbols
25
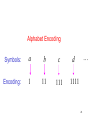
Alphabet Encoding
Symbols:
a
b
c
d
Encoding:
1
11
111
1111

26
State Encoding
States:
q1
q2
q3
q4
Encoding:
1
11
111
1111

Head Move Encoding
Move:
L
R
Encoding:
1
11
27
Transition Encoding
Transition:
 (q1, a)  (q2 , b, L)
Encoding:
1 0 1 0 11 0 11 0 1
separator
28
Machine Encoding
Transitions:
 (q1, a)  (q2 , b, L)
 (q2 , b)  (q3 , c, R)
Encoding:
1 0 1 0 11 0 11 0 1 00 11 0 110 111 0 111 0 11
separator
29
Tape 1 contents of Universal Turing Machine:
encoding of the simulated machine
as a binary string of 0’s and 1’s
M
30
A Turing Machine is described
with a binary string of 0’s and 1’s.
Therefore:
The set of Turing machines forms a language:
Each string of the language is
the binary encoding of a Turing Machine.
31
Language of Turing Machines
L = { 010100101,
(Turing Machine 1)
00100100101111,
111010011110010101,
(Turing Machine 2)
……
…… }
32
The Chomsky Hierarchy
33
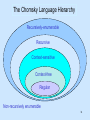
The Chomsky Language Hierarchy
Recursively-enumerable
Recursive
Context-sensitive
Context-free
Regular
Non-recursively enumerable
34
Unrestricted Grammars
Productions
uv
String of variables
and terminals
String of variables
and terminals
35
Example of unrestricted grammar
S  aBc
aB  cA
Ac  d
36
Theorem
A language L is recursively enumerable
if and only if it is generated by an
unrestricted grammar.
37
Context-Sensitive Grammars
Productions
uv
String of variables
and terminals
and
String of variables
and terminals
|u|  |v|
38
The language
n n n
{a b c }
is context-sensitive:
S  aBSc
S 
Ba  aB
Bc  bc
Bb  bb
39
Theorem
A language L is context sensitive
if and only if
it is accepted by a Linear-Bounded
automaton.
40
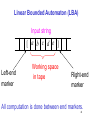
Linear Bounded Automata (LBAs)
are the same as Turing Machines
with one difference:
The input string tape space
is the only tape space allowed to use.
41
Linear Bounded Automaton (LBA)
Input string
[ a b c d e ]
Left-end
marker
Working space
in tape
Right-end
marker
All computation is done between end markers.
42
Observation
There is a language which is context-sensitive
but not recursive.
43
Decidability
44
Consider problems with answer YES or NO.
Examples
• Does Machine
• Is string
M have three states ?
w a binary number?
• Does DFA
M accept any input?
45
A problem is decidable if some Turing machine
solves (decides) the problem.
Decidable problems:
• Does Machine M have three states ?
• Is string
w a binary number?
• Does DFA
M accept any input?
46
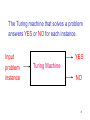
The Turing machine that solves a problem
answers YES or NO for each instance.
Input
problem
instance
YES
Turing Machine
NO
47
The machine that decides a problem:
• If the answer is YES
then halts in a yes state
• If the answer is NO
then halts in a no state
These states may not be the final states.
48
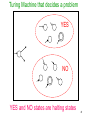
Turing Machine that decides a problem
YES
NO
YES and NO states are halting states
49
Difference between
Recursive Languages (“Acceptera”) and
Decidable problems (“Avgöra”)
For decidable problems:
The YES states may not be final states.
50
Some problems are undecidable:
There is no Turing Machine that
solves all instances of the problem.
51
A famous undecidable problem:
The halting problem
52
The Halting Problem
Input: • Turing Machine
• String w
M
Question: Does M halt on w ?
53
Theorem
The halting problem is undecidable.
Proof
Assume to the contrary that
the halting problem is decidable.
54
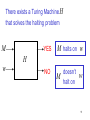
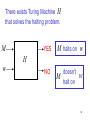
There exists a Turing Machine H
that solves the halting problem
M
YES
M halts on w
NO
doesn’t
halt on
H
w
M
w
55
Construction of
H
Input:
initial tape contents
wM w
q y YES
q0
qn NO
Encoding
of M
String
w
H
56
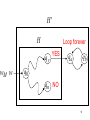
Construct machine
H
If H returns YES then loop forever.
If H returns NO then halt.
57
H
H
Loop forever
qy
wM w
YES
qa
qb
q0
qn NO
58
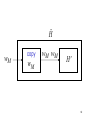
Construct machine
Input:
If
wM
Ĥ
(machine
M)
M halts on input wM
Then loop forever
Else halt
59
Ĥ
wM
copy
wM
wM wM
H
60
Run machine
Input:
If
Ĥ with input itself
wHˆ
(machine
Ĥ )
Ĥ halts on input wHˆ
Then loop forever
Else halt
61
Ĥ on input wHˆ :
If
Ĥ halts then Ĥ loops forever.
If
Ĥ doesn’t halt then Ĥ halts.
CONTRADICTION !
62
This means that
The halting problem is undecidable.
END OF PROOF
63
Another proof of the same theorem
If the halting problem was decidable then
every recursively enumerable language
would be recursive.
64
Theorem
The halting problem is undecidable.
Proof
Assume to the contrary that
the halting problem is decidable.
65
There exists Turing Machine H
that solves the halting problem.
M
YES
M halts on w
NO
doesn’t
halt on
H
w
M
w
66
Let
L be a recursively enumerable language.
Let
M be the Turing Machine that accepts L .
We will prove that
L is also recursive:
We will describe a Turing machine that
accepts L and halts on any input.
67
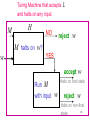
Turing Machine that accepts L
and halts on any input
M
H
NO
reject
w
M halts on w?
w
YES
accept
Run M
with input
w
Halts on final state
w
reject
w
Halts on non-final
68
state
Therefore
L is recursive.
Since L is chosen arbitrarily, we have
proven that every recursively enumerable
language is also recursive.
But there are recursively enumerable
languages which are not recursive.
Contradiction!
69
Therefore, the halting problem is undecidable.
END OF PROOF
70
A simple undecidable problem:
The Membership Problem
71
The Membership Problem
Input: • Turing Machine M
• String
w
Question: Does M accept w ?
72
Theorem
The membership problem is undecidable.
Proof
Assume to the contrary that
the membership problem is decidable.
73
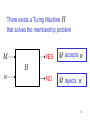
There exists a Turing Machine H
that solves the membership problem
M
YES
M accepts w
NO
M rejects w
H
w
74
Let
L be a recursively enumerable language.
Let
M be the Turing Machine that accepts L .
We will prove that
L is also recursive:
We will describe a Turing machine that
accepts L and halts on any input.
75
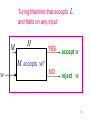
Turing Machine that accepts
and halts on any input
M
H
L
YES
accept w
NO
reject
M accepts w?
w
w
76
Therefore,
L is recursive.
Since L is chosen arbitrarily, we have
proven that every recursively enumerable
language is also recursive.
But there are recursively enumerable
languages which are not recursive.
Contradiction!
77
Therefore, the membership problem
is undecidable.
END OF PROOF
78
Reducibility
79
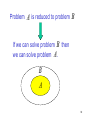
Problem
A
is reduced to problem
B
If we can solve problem B then
we can solve problem A .
B
A
80
Problem
If
If
A
is reduced to problem
B
B is decidable then A is decidable.
A is undecidable then B is undecidable.
81
Example
the halting problem
reduced to
the state-entry problem.
82
The state-entry problem
Inputs: •Turing Machine
•State
M
q
•String w
Question:
M enter state q
on input w ?
Does
83
Theorem
The state-entry problem is undecidable.
Proof
Reduce the halting problem to
the state-entry problem.
84
Suppose we have an algorithm
(Turing Machine)
that solves the state-entry problem.
We will construct an algorithm
that solves the halting problem.
85
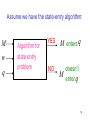
Assume we have the state-entry algorithm:
M
w
q
Algorithm for
state-entry
problem
YES
NO
M enters q
M
doesn’t
enter q
86
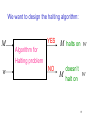
We want to design the halting algorithm:
M
w
YES
M halts on w
NO
doesn’t
halt on
Algorithm for
Halting problem
M
w
87
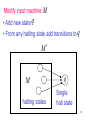
Modify input machine
M
• Add new state q
• From any halting state add transitions to q
M
M
halting states
q
Single
halt state
88
M halts
if and
only if
M  halts on state q
89
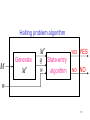
Algorithm for halting problem
Inputs: machine
M and string w
1. Construct machine
M  with state q
2. Run algorithm for state-entry problem
with inputs: M  , q , w
90
Halting problem algorithm
M
Generate
M
M
q State-entry
w
algorithm
YES
YES
NO
NO
w
91
We reduced the halting problem
to the state-entry problem.
Since the halting problem is undecidable,
it must be that the state-entry problem
is also undecidable.
END OF PROOF
92
Another example
The halting problem
reduced to
the blank-tape halting problem.
93
The blank-tape halting problem
Input:
Turing Machine
Question: Does
M
M halt when started with
a blank tape?
94
Theorem
The blank-tape halting problem is undecidable.
Proof
Reduce the halting problem to the
blank-tape halting problem.
95
Suppose we have an algorithm
for the blank-tape halting problem.
We will construct an algorithm
for the halting problem.
96
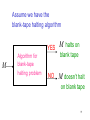
Assume we have the
blank-tape halting algorithm
YES
M
Algorithm for
blank-tape
halting problem
M halts on
blank tape
NO
M doesn’t halt
on blank tape
97
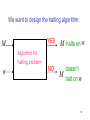
We want to design the halting algorithm:
YES
M
M halts on w
Algorithm for
halting problem
w
NO
M
doesn’t
halt on w
98
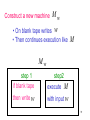
Construct a new machine
Mw
• On blank tape writes w
• Then continues execution like
M
Mw
step 1
if blank tape
then write w
step2
M
with input w
execute
99
M halts on input string w
if and
only if
M w halts when started with blank tape.
100
Algorithm for halting problem
Inputs: machine
M and string w
1. Construct M w
2. Run algorithm for
blank-tape halting problem
with input M w
101
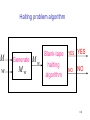
Halting problem algorithm
M
w
Generate
Mw
Mw
Blank-tape
halting
algorithm
YES
YES
NO
NO
102
We reduced the halting problem
to the blank-tape halting problem.
Since the halting problem is undecidable,
the blank-tape halting problem is
also undecidable.
END OF PROOF
103
Summary of Undecidable Problems
Halting Problem
Does machine
M halt on input w ?
Membership problem
Does machine M accept string w ?
(In other words: Is a string
w member of a
recursively enumerable language L ?)
104
Blank-tape halting problem
Does machine M halt when starting
on blank tape?
State-entry Problem:
Does machine
on input w ?
M enter state q
105
Uncomputable Functions
106
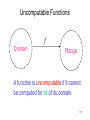
Uncomputable Functions
f
Domain
Range
A function is uncomputable if it cannot
be computed for all of its domain.
107
Example
An uncomputable function:
f (n) 
maximum number of moves until
any Turing machine with n states
halts when started with the blank tape.
108
Theorem
Function
f (n) is uncomputable.
Proof
Assume to the contrary that
f (n) is computable.
Then the blank-tape halting problem
is decidable.
109
Algorithm for blank-tape halting problem
Input: machine
1. Count states of
M
M: m
f (m)
3. Simulate M for f (m) steps
2. Compute
starting with empty tape
If
M halts then return YES
otherwise return NO
110
Therefore, the blank-tape halting
problem must be decidable.
However, we know that the blank-tape
halting problem is undecidable.
Contradiction!
111
Therefore, function
f (n) is uncomputable.
END OF PROOF
112
Definition
A language L is recursively enumerable if
There is a Turing machine M accepting all
Strings w in L. This is denoted L=L(M)
A language L is recursive if there is a Turing
Machine M, that halts on any input w and
deciding weather w is in L or not.
113
Another definition
A language L is recursively enumerable iff it
Is generated by an unrestricted grammar.
114
Implication
A language L is recursive iff L is recursively
enumerable AND it’s complement L’ is
recursively enumerable
115
Proof sketch (if)
Let L be a recursive language. Then there is
A Turing machine M such that running any
input w on M, M will answer yes if w is in L
and no if w is not in L.
Construct a machine ML accepting L by
modifying M such as the yes state is a final
state (all other rejecting).
Construct a machine ML’ accepting L’ by
modifying M such that the no state is a final
state (all other rejecting).
116
Proof sketch (only if)
Let M be a Turing machine accepting L
and let M’ be a Turing machine accepting L’
Let ML be the Turing machine deciding L.
Run M and M’ in parallel on input w.
One of the machines will accept w.
Let ML answer yes if M accepts, and no if M’
Accepts. Since ML clearly can be constructed.
L is a recursive language.
117
Not all recursive languages are recursively
enumerable
Let ∑ = {a}. Let H be the set of all Turing
Machines with this alphabet. Note that H is
countably infinite! Thus, H = {M0,M1,M2,…}
Let L(Mi) denote the recursively enumerable
Language of Mi (that is, the set of strings that
Drives Mi into a final state.)
118
Not all recursive languages are recursively
enumerable
Let L  {a | a  L( M i )}
L is recursively enumerable.
Pseudo-code:
1. Find i by counting a’s in w
2. Find Mi by the known encoding
3. Run Mi with w. Accept if Mi accepts
i
i
119
Not all recursive languages are recursively
enumerable
Let L  {a | a  L( M i )}
L’ is not recursively enumerable. Assume for
contradiction it is: there is a TM M’ that
Accepts w if w is in L’.
Note: M’ has {a} as alphabet, so M’ = Mk for
some integer k.
i
i
120
Not all recursive languages are recursively
enumerable
i
i
L  {a | a  L( M i )}
Let Mk be the machine accepting L’. That is
L’ = L(Mk).
Let w  a
Is w in L’?
k
121
Not all recursive languages are recursively
enumerable
i
i
L  {a | a  L( M i )}
Let Mk be the machine accepting L’. That is
L’ = L(Mk).
w  L  w  L( M k )  L
w  L  w  L( M k )  L
Contradiction!! L’ is not RE
122
Not all recursive languages are recursively
enumerable
L’ is not RE, but L is. According to previous
Result a language is recursive iff L and L’ is
RE.
Conclusion: L is recursively enumerable
but not recursive.
123
Rice’s Theorem
124
Definition
Non-trivial properties of
recursively enumerable languages:
any property possessed by some (not all)
recursively enumerable languages.
125
Some non-trivial properties of
recursively enumerable languages:
• L is empty
• L is finite
• L contains two different strings
of the same length
126
Rice’s Theorem
Any non-trivial property of
a recursively enumerable language
is undecidable.
127
We will prove some non-trivial properties
without using Rice’s theorem.
128
Theorem
For any recursively enumerable language L
it is undecidable whether it is empty.
Proof
We will reduce the membership problem
to the problem of deciding whether L
is empty.
129
Membership problem:
Does machine M accept string w?
130
Let
M be the machine that accepts L
L( M )  L
Assume we have the empty language algorithm:
M
Algorithm for
empty language
problem
YES
L(M ) empty
NO
L(M ) not empty
131
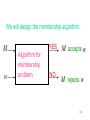
We will design the membership algorithm:
M
w
YES
Algorithm for
membership
problem
NO
M accepts w
M rejects w
132
First construct machine
Mw :
When M enters a final state,
compare original input string with w.
Accept if original input is
the same as w.
M
Construct
w
Mw
133
w L
if and
only if
L( M w ) is not empty
L( M w )  {w}
134
Algorithm for membership problem
Inputs: machine
1. Construct
M and string w
Mw
2. Determine if
L( M w ) is empty
YES: then
w L(M )
NO: then
w L(M )
135
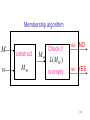
Membership algorithm
M
w
construct
Mw
Mw
Check if
YES
NO
NO
YES
L( M w )
is empty
136
We reduced the empty language problem
to the membership problem.
Since the membership problem is undecidable,
the empty language problem is
also undecidable.
END OF PROOF
137
Decidability
…continued…
138
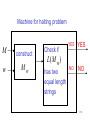
Theorem
For a recursively enumerable language
it is undecidable to determine whether
L is finite.
L
Proof
We will reduce the halting problem
to the finite language problem.
139
Let
M be the machine that accepts L
L( M )  L
Assume we have the finite language algorithm:
M
Algorithm for
finite language
problem
YES
L(M ) finite
NO
L(M ) not finite
140
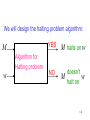
We will design the halting problem algorithm:
YES
M
Algorithm for
Halting problem
w
NO
M halts on w
M
doesn’t
w
halt on
141
First construct machine
Mw .
Initially, simulates M on input w.
When M enters a halt state,
accept any input (infinite language).
Otherwise accept nothing (finite language).
142
M halts on w
if and
only if
L( M w ) is not finite.
143
Algorithm for halting problem:
Inputs: machine
1. Construct
M and string w
Mw
2. Determine if
L( M w ) is finite
YES: then
M doesn’t halt on w
NO: then M halts on w
144
Machine for halting problem
M
w
construct
Mw
Check if
YES
L( M w )
is finite
NO
NO
YES
145
We reduced the finite language problem
to the halting problem.
Since the halting problem is undecidable,
the finite language problem is
also undecidable.
END OF PROOF
146
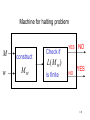
Theorem
For a recursively enumerable language L
it is undecidable whether L contains
two different strings of same length.
Proof
We will reduce the halting problem
to the two strings of equal length- problem.
147
Let
M be the machine that accepts L
L( M )  L
Assume we have the two-strings algorithm:
YES
M
Algorithm for
two-strings
problem
NO
L(M ) contains
L(M )
doesn’t
contain
two equal length strings
148
We will design the halting problem algorithm:
M
Algorithm for
Halting problem
w
YES
M halts on w
NO
doesn’t
halt on
M
w
149
First construct machine
Initially, simulates
M w.
M on input w.
When M enters a halt state,
accept symbols a or b .
(two equal length strings)
150
M halts on w
if and
only if
M w accepts a and b
(two equal length strings)
151
Algorithm for halting problem
Inputs: machine
1. Construct
M and string w
Mw
2. Determine if M w accepts
two strings of equal length
M halts on w
NO: then M doesn’t halt on w
YES: then
152
Machine for halting problem
M
w
construct
Mw
Check if
YES
YES
NO
NO
L( M w )
has two
equal length
strings
153
We reduced the two strings of equal length problem to the halting problem.
Since the halting problem is undecidable,
the two strings of equal length problem is
also undecidable.
END OF PROOF
154
Rices theorem
If  is a set of recursively enumerable
languages containing some but not all such
languages, then no TM can decide for an
arbitrary Recursively enumerable language
L, if L belongs to  or not.
155
Example
Given a Turing Machine M, is it
possible to decide weather all strings
acceted by M begins and ends with
the same symbol?
156
Undecidable
The problem is about a non-trivial
language property. There are recursively
enumerable languages with this property
and there are recursively enumerable
langages without this property.
157
Formally:
 = { L | L is a recursively enumerable
language where all strings begin and end
with the same symbol }
158
Interaction:
Conjectures, Results, and Myths
Dina Goldin
Univ. of Connecticut, Brown University
http://www.cse.uconn.edu/~dqg
159
Fundamental Questions
Underlying Theory of Computation
What is computation?
How do we model it?
160
Shared Wisdom
(from our undergraduate Theory of Computation courses)
computation: finite transformation
of input to output
input: finite size (e.g. string or
number)
closed system: all input available
at start, all output generated at end
Mathematical worldview:
All computable problems
are function-based.
behavior: functions, transformation
of input data to output data
Church-Turing thesis: Turing
Machines capture this (algorithmic)
notion of computation
161
The Mathematical Worldview
“The theory of computability and non-computability [is] usually
referred to as the theory of recursive functions... the notion of TM has
been made central in the development."
Martin Davis, Computability & Unsolvability, 1958
“Of all undergraduate CS subjects, theoretical computer science has
changed the least over the decades.”
SIGACT News, March 2004
“A TM can do anything that a computer can do.”
Michael Sipser, Introduction to the Theory of Computation, 1997
162
The Operating System
Conundrum
Real programs, such as
operating systems and word
processors, often receive an
unbounded amount of input
over time, and never "finish"
their task. Turing machines
do not model such ongoing
computation well…
[TM entry, Wikipedia]
If a computation
does not terminate,
it’s “useless” –
but aren’t OS’s
useful??
163
Rethinking Shared Wisdom:
(what do computers do?)
computation: finite transformation
of input to output
computation: ongoing process which
performs a task or delivers a service
input: finite-size (string or number) dynamically generated stream of input
tokens (requests, percepts, messages)
open system: later inputs depend on
closed system: all input available at
earlier outputs and vice versa (I/O
start, all output generated at end
entanglement, history dependence)
behavior: functions, algorithmic
transformation of input data to
output data
behavior: processes, components,
control devices, reactive systems,
intelligent agents
Church-Turing thesis: Turing
Wegner’s conjecture: Interaction is
Machines capture this (algorithmic) more powerful than algorithms
notion of computation
164
Example:
Driving home from work
Algorithmic input: a description of the world (a static “map”)
Output: a sequence of pairs of #s (time-series data)
- for turning the wheel
- for pressing gas/break
Similar to classic AI search/planning problems.
165
Driving home from work (cont.)
But… in a real-world environment, the output depends
on every grain of sand in the road (chaotic behavior).
?
Can we possibly have a map that’s detailed enough?
Worse yet… the domain is dynamic. The output
depends on weather conditions, and on other drivers and
pedestrians.
We can’t possibly be expected to predict that in advance!
Nevertheless the problem is solvable!
Google “autonomous vehicle research”
166
Driving home from work (cont.)
The problem is solvable interactively.
Interactive input: stream of video camera images, gathered
as we are driving
Output: the desired time-series data, generated
as we are driving
similar to control systems, or online computation
A paradigm shift in the conceptualization of computational problem solving.
167
Outline
• Rethinking the mathematical worldview
• Persistent Turing Machines (PTMs)
• PTM expressiveness
• Sequential Interaction
– Sequential Interaction Thesis
• The Myth of the Church-Turing Thesis
– the origins of the myth
• Conclusions and future work
168
Sequential Interaction
• Sequential interactive computation:
system continuously interacts with its environment
by alternately accepting an input string
and computing a corresponding output string.
• Examples:
- method invocations of an object instance
in an OO language
- a C function with static variables
- queries/updates to single-user databases
- recurrent neural networks
- control systems
- online computation
- transducers
- dynamic algorithms
- embedded systems
169
Sequential Interaction Thesis
Whenever there is an effective method for performing
sequential interactive computation, this computation
can be performed by a Persistent Turing Machine
• Universal PTM: simulates any other PTM
– Need additional input describing the PTM (only once)
• Example: simulating Answering Machine
(simulate AM, will-do),
(record hello, ok), (erase, done), (record John, ok),
(record Hopkins, ok), (playback, John Hopkins), …
Simulation of other sequential interactive systems is analogous.
170
Church-Turing Thesis Revisited
•
Church-Turing Thesis:
Whenever there is an effective method
for obtaining the values of a mathematical function,
the function can be computed by a Turing Machine
• Common Reinterpretation (Strong Church-Turing Thesis)
A TM can do (compute) anything that a computer can do
• The equivalence of the two is a myth
– the function-based behavior of algorithms does not capture all
forms of computation
– this myth has been dogmatically accepted by the CS community
•
Turing himself would have denied it
– in the same paper where he introduced what we now call Turing
Machines, he also introduced choice machines, as a distinct model
of computation
– choice machines extend Turing Machines to interaction by allowing
a human operator to make choices during the computation.
171
Origins of the Church-Turing Thesis Myth
A TM can do anything that a computer can do.
Based on several claims:
1. A problem is solvable if there exists a Turing Machine
for computing it.
2. A problem is solvable if it can be specified by an algorithm.
3. Algorithms are what computers do.
Each claim is correct in isolation
provided we understand the underlying assumptions
Together, they induce an incorrect conclusion
TMs = solvable problems = algorithms = computation
172
Deconstructing the Turing Thesis Myth (1)
TMs = solvable problems
• Assumes:
All computable problems are function-based.
• Reasons:
– Theory of Computation started as a field of mathematics;
mathematical principles were adopted for the fundamental
notions of computation, identifying computability with the
computation of functions, as well as with Turing Machines.
– The batch-based modus operandi of original computers did
not lend itself to other conceptualizations of computation.
173
Deconstructing the Turing Thesis Myth (2)
solvable problems = algorithms
Assumes:
- Algorithmic computation is also function based;
i.e., the computational role of an algorithm
is to transform input data to output data.
• Reasons:
– Original (mathematical) meaning of “algorithms”
E.g. Euclid’s greatest common divisor algorithm
– Original (Knuthian) meaning of “algorithms”
“An algorithm has zero or more inputs, i.e., quantities which are
given to it initially before the algorithm begins.“
[Knuth’68]
174
Deconstructing the Turing Thesis Myth (3)
algorithms = computation
• Reasons:
– The ACM Curriculum (1968): Adopted algorithms as the central
concept of CS without explicit agreement on the meaning of this term.
– Textbooks: When defining algorithms, the assumption of their closed
function-based nature was often left implicit, if not forgotten
“An algorithm is a recipe, a set of instructions or the specifications
of a process for doing something. That something is usually solving
a problem of some sort.”
[Rice&Rice’69]
“An algorithm is a collection of simple instructions for carrying out
some task. Commonplace in everyday life, algorithms sometimes
are called procedures or recipes...”
[Sipser’97]
175
Outline
• Rethinking the mathematical worldview
• Persistent Turing Machines (PTMs)
• PTM expressiveness
• Sequential Interaction
• The Myth of the Church-Turing Thesis
• Conclusions and future work
176
The Shift to Interaction in CS
Algorithmic
Interactive
Computation = transforming
input to output
Computation = carrying out a
task over time
Logic and search in AI
Intelligent agents, partially
observable environments, learning
Procedure-oriented
programming
Object-oriented programming
Closed systems
Open systems
Compositional behavior
Emergent behavior
Rule-based reasoning
Simulation, control, semi-Markov
processes
177
The Interactive Turing Test
• From answering questions to holding discussions.
• Learning from -- and adapting to -- the questioner.
• “Book intelligence” vs. “street smarts”.
“It is hard to draw the line at what is intelligence and what is
environmental interaction. In a sense, it does not really matter
which is which, as all intelligent systems must be situated in some
world or other if they are to be useful entities.” [Brooks]
178
Modeling Interactive Computation:
PTMs in Perspective
• Many other interactive models
– Reactive [MP] and embedded systems
– Dataflow, I/O automata [Lynch], synchronous languages, finite/pushdown
automata over infinite words
– Interaction games [Abramsky], online algorithms [Albers]
– TM extensions: on-line Turing machines [Fischer], interactive Turing
machines [Goldreich]...
• Concurrency Theory
– Focuses on communication (between concurrent agents/processes) rather
than computation [Milner]
– Orthogonal to the theory of computation and TMs.
• What makes PTMs unique?
– Provably more expressive than TMs.
– Bridging the gap between concurrency theory (labeled transition systems)
and traditional TOC.
179
Future Work: 3 conjectures
• Theory of Sequential Interaction
conjecture: notions analogous to computational
complexity, logic, and recursive functions can be
developed for sequential interaction computation
• Multi-stream interaction
– From hidden variables to hidden interfaces
conjecture: multi-stream interaction is more
powerful than sequential interaction [Wegner’97]
• Formalizing indirect interaction
– Interaction via persistent, observable changes to the
common environment
– In contrast to direct interaction (via message passing)
conjecture: direct interaction does not capture all
forms of multi-agent behaviors
180
References
http://www.cse.uconn.edu/~dqg/papers/
[Wegner’97] Peter Wegner
Why Interaction is more Powerful than Algorithms
Communications of the ACM, May 1997
[EGW’04] Eugene Eberbach, Dina Goldin, Peter Wegner
Turing's Ideas and Models of Computation
book chapter, in Alan Turing: Life and Legacy of a Great Thinker, Springer
2004
[I&C’04] Dina Goldin, Scott Smolka, Paul Attie, Elaine Sonderegger
Turing Machines, Transition Systems, and Interaction
Information & Computation Journal, 2004
[GW’04] Dina Goldin, Peter Wegner
The Church-Turing Thesis: Breaking the Myth
presented at CiE 2005, Amsterdam, June 2005
to be published in LNCS
181