* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Lines that intersect Circles
Mirror symmetry (string theory) wikipedia , lookup
Pythagorean theorem wikipedia , lookup
Conic section wikipedia , lookup
Analytic geometry wikipedia , lookup
Duality (projective geometry) wikipedia , lookup
Steinitz's theorem wikipedia , lookup
Cartan connection wikipedia , lookup
Line (geometry) wikipedia , lookup
Affine connection wikipedia , lookup
Metric tensor wikipedia , lookup
Euclidean geometry wikipedia , lookup
Differentiable manifold wikipedia , lookup
Trigonometric functions wikipedia , lookup
History of trigonometry wikipedia , lookup
Lie sphere geometry wikipedia , lookup
Riemannian connection on a surface wikipedia , lookup
Problem of Apollonius wikipedia , lookup
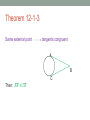
LINES THAT INTERSECT CIRCLES Geometry CP2 (Holt 12-1) K. Santos Circle definition Circle: points in a plane that are a given distance (radius) from a given point (center). Circle P Radius: center to a point on the circle P Interior & Exterior of a circle Interior of a circle: points inside the circle Exterior of a circle: points outside the circle exterior interior Lines & Segments that intersect a circle A G F E O B C D Chord: is a segment whose endpoints lie on a circle. Diameter: -a chord that contains the center -connects two points on the circle and passes through the center Secant: line that intersects a circle at two points Tangent • A tangent to a circle is a line in the plane of the circle that intersects the circle in exactly one point 𝐴𝐵 • The point where a circle and a tangent intersect is the point of tangency Point B A B Pairs of circles Congruent Circles: two circles that have congruent radii Concentric Circles: coplanar circles with the same center Tangent Circles Tangent Circles: coplanar circles that intersect at exactly one point Internally tangent circles externally tangent circles Common Tangent Common tangent: a line that is tangent to two circles Common external tangents common internal tangents Theorems 12-1-1 & 12-1-2 Radius perpendicular to tangent line (at point of tangency) O A 𝐴𝐵⟘𝑂𝑃 P B Example 𝐸𝐷 is tangent to circle O. Radius is 5” and ED = 12” Find the length of 𝑂𝐷 . O E D Remember Pythagorean theorem (let 𝑂𝐷 = x) 𝑥 2 = 52 + 122 𝑥 2 = 25 + 144 𝑥 2 = 169 x= 169 x = 13 Example—Is there a tangent line? Determine if there is a tangent line? 12 8 6 If there is a tangent then there must have been a right angle (in a right triangle). Test for a right angle. 122 62 + 82 144 36 + 64 144 ≠100 so there is no right angle, no tangent line Example Find x. 130° x Radius ⊥ tangents (right angles) Sum of the angles in a quadrilateral are 360° 90 + 90 + 130 = 310 x = 360 - 310 x = 50° Theorem 12-1-3 Same external point tangents congruent A B C Then: 𝐴𝐵 ≅ 𝐶𝐵 Example: R 𝑅𝑇 and 𝑅𝑆 are tangent to circle Q. Find RS. 2n – 1 T RT = RS 2n – 1 = n + 3 n–1=3 n=4 RS = n + 3 RS = 4 + 3 RS = 7 n+3 S