I. Topological background
... of differential equations do not have solutions that can be expressed using simple formulas from calculus. In particular, one cannot do this for the classical Three Body Problem in celestial mechanics, which grow systems comprised of just three objects. In this course it will be necessary to work wi ...
... of differential equations do not have solutions that can be expressed using simple formulas from calculus. In particular, one cannot do this for the classical Three Body Problem in celestial mechanics, which grow systems comprised of just three objects. In this course it will be necessary to work wi ...
THE GEOMETRIES OF 3
... direction in £ 3 . But groups acting non-freely on £ 3 certainly need not leave any direction invariant. For example, the symmetry group of a cube acts on £ 3 fixing the origin and plainly leaves no direction invariant. I will now describe the contents of this article in greater detail. In §1,1 disc ...
... direction in £ 3 . But groups acting non-freely on £ 3 certainly need not leave any direction invariant. For example, the symmetry group of a cube acts on £ 3 fixing the origin and plainly leaves no direction invariant. I will now describe the contents of this article in greater detail. In §1,1 disc ...
Exotic spheres and curvature - American Mathematical Society
... five, any smooth manifold with the homotopy type of a sphere must be homeomorphic to a sphere. This is the Generalised Poincaré Conjecture, proved by Smale in [Sm1]. Thus in these dimensions the set of diffeomorphism classes of homotopy spheres is precisely the union of the diffeomorphism class of the ...
... five, any smooth manifold with the homotopy type of a sphere must be homeomorphic to a sphere. This is the Generalised Poincaré Conjecture, proved by Smale in [Sm1]. Thus in these dimensions the set of diffeomorphism classes of homotopy spheres is precisely the union of the diffeomorphism class of the ...
Symplectic structures -- a new approach to geometry.
... shows that X is symplectic exactly when the corresponding 1-form α = ιX ω is closed. Since every manifold supports many closed 1-forms, the group Symp(M, ω) of all symplectomorphisms is infinite-dimensional. It has a normal subgroup Ham(M, ω) that corresponds to the exact 1-forms α = dH. By definiti ...
... shows that X is symplectic exactly when the corresponding 1-form α = ιX ω is closed. Since every manifold supports many closed 1-forms, the group Symp(M, ω) of all symplectomorphisms is infinite-dimensional. It has a normal subgroup Ham(M, ω) that corresponds to the exact 1-forms α = dH. By definiti ...
as a PDF - Universität Bonn
... S(M ) is the following. The topological group Diff(M ) appears as the structural group of oriented smooth surface bundles; and the contractibility of S(M ) shows that on any surface bundle E → B, we can find complex structures on the fibers which vary continuously. Moreover, all these complex struct ...
... S(M ) is the following. The topological group Diff(M ) appears as the structural group of oriented smooth surface bundles; and the contractibility of S(M ) shows that on any surface bundle E → B, we can find complex structures on the fibers which vary continuously. Moreover, all these complex struct ...
4a.pdf
... Let M be any hyperbolic manifold obtained by gluing polyhedra with some vertices at infinity, and let K be the complex obtained by including the ideal vertices. The completion M̄ is obtained by completing a deleted neighborhood N(v) of each ideal vertex v in k, and gluing these completed neighborhoo ...
... Let M be any hyperbolic manifold obtained by gluing polyhedra with some vertices at infinity, and let K be the complex obtained by including the ideal vertices. The completion M̄ is obtained by completing a deleted neighborhood N(v) of each ideal vertex v in k, and gluing these completed neighborhoo ...
A geometric proof of the Berger Holonomy Theorem
... of locally symmetric, totally geodesic submanifolds (whose tangent spaces generate Tp M ). In this way, the Jacobi operator must diagonalize, with constant coefficients, in a parallel frame. Hence M is locally symmetric at p. 2. Preliminaries and basic facts In this section we will briefly recall some ...
... of locally symmetric, totally geodesic submanifolds (whose tangent spaces generate Tp M ). In this way, the Jacobi operator must diagonalize, with constant coefficients, in a parallel frame. Hence M is locally symmetric at p. 2. Preliminaries and basic facts In this section we will briefly recall some ...
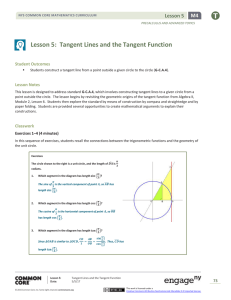
Apply the Tangent Ratio
... the lengths of two sides in a right triangle. Tangent The ratio of the length of the leg opposite an acute angle in a right triangle to the length of the leg adjacent to the angle is the tangent of the ...
... the lengths of two sides in a right triangle. Tangent The ratio of the length of the leg opposite an acute angle in a right triangle to the length of the leg adjacent to the angle is the tangent of the ...
Unlocking the geometry of polygon space by taking square roots
... ~ 1 and w ~ 2 are called the The angles between ~v1 and ~v2 and w Jordan angles between the two planes. The rotation carrying ~v1 → ~v2 and w ~1 → w ~ 2 is called the direct rotation from P1 to P2 and it is the shortest path from P1 to P2 in the Grassmann manifold G2 (Rn ). ...
... ~ 1 and w ~ 2 are called the The angles between ~v1 and ~v2 and w Jordan angles between the two planes. The rotation carrying ~v1 → ~v2 and w ~1 → w ~ 2 is called the direct rotation from P1 to P2 and it is the shortest path from P1 to P2 in the Grassmann manifold G2 (Rn ). ...
MAT1360: Complex Manifolds and Hermitian Differential Geometry
... A “complex manifold” is a smooth manifold, locally modelled on the complex Euclidean space Cn and whose transition functions are holomorphic. More precisely, a complex manifold is a pair (M, J) consisting of a smooth, real manifold of real dimension 2n and a maximal atlas whose overlap maps lie in t ...
... A “complex manifold” is a smooth manifold, locally modelled on the complex Euclidean space Cn and whose transition functions are holomorphic. More precisely, a complex manifold is a pair (M, J) consisting of a smooth, real manifold of real dimension 2n and a maximal atlas whose overlap maps lie in t ...
Differential Topology
... This phenomenon is quite common: locally you can represent things by means of “charts”, but the global character can’t be represented by one single chart. You need an entire atlas, and you need to know how the charts are to be assembled, or even better: the charts overlap so that we know how they al ...
... This phenomenon is quite common: locally you can represent things by means of “charts”, but the global character can’t be represented by one single chart. You need an entire atlas, and you need to know how the charts are to be assembled, or even better: the charts overlap so that we know how they al ...
Differentiable manifold

In mathematics, a differentiable manifold is a type of manifold that is locally similar enough to a linear space to allow one to do calculus. Any manifold can be described by a collection of charts, also known as an atlas. One may then apply ideas from calculus while working within the individual charts, since each chart lies within a linear space to which the usual rules of calculus apply. If the charts are suitably compatible (namely, the transition from one chart to another is differentiable), then computations done in one chart are valid in any other differentiable chart.In formal terms, a differentiable manifold is a topological manifold with a globally defined differential structure. Any topological manifold can be given a differential structure locally by using the homeomorphisms in its atlas and the standard differential structure on a linear space. To induce a global differential structure on the local coordinate systems induced by the homeomorphisms, their composition on chart intersections in the atlas must be differentiable functions on the corresponding linear space. In other words, where the domains of charts overlap, the coordinates defined by each chart are required to be differentiable with respect to the coordinates defined by every chart in the atlas. The maps that relate the coordinates defined by the various charts to one another are called transition maps.Differentiability means different things in different contexts including: continuously differentiable, k times differentiable, smooth, and holomorphic. Furthermore, the ability to induce such a differential structure on an abstract space allows one to extend the definition of differentiability to spaces without global coordinate systems. A differential structure allows one to define the globally differentiable tangent space, differentiable functions, and differentiable tensor and vector fields. Differentiable manifolds are very important in physics. Special kinds of differentiable manifolds form the basis for physical theories such as classical mechanics, general relativity, and Yang–Mills theory. It is possible to develop a calculus for differentiable manifolds. This leads to such mathematical machinery as the exterior calculus. The study of calculus on differentiable manifolds is known as differential geometry.