Convex Sets and Convex Functions on Complete Manifolds
... Small convex sets such as strongly convex balls are used in the proofs of finiteness theorems. Weinstein's theorem [18], which is the first attempt in this direction, states that given n and (56(0, 1), there are only finitely many homotopy types of 2/7-dimensional simply connected <5-pinched manifol ...
... Small convex sets such as strongly convex balls are used in the proofs of finiteness theorems. Weinstein's theorem [18], which is the first attempt in this direction, states that given n and (56(0, 1), there are only finitely many homotopy types of 2/7-dimensional simply connected <5-pinched manifol ...
Lesson 12 - EngageNY
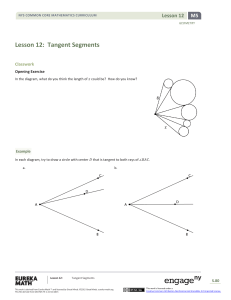
... Construct as many circles as you can that are tangent to both the given angles at the same time. You can extend the rays as needed. These two angles share a side. ...
... Construct as many circles as you can that are tangent to both the given angles at the same time. You can extend the rays as needed. These two angles share a side. ...
introduction to algebraic topology and algebraic geometry
... de Rham cohomology of X out of the de Rham cohomology of X1 and X2 (Künneth theorem, cf. [3]). For later use, we prove here a very particular case. This will serve also as an example of the notion of homotopy between complexes. ...
... de Rham cohomology of X out of the de Rham cohomology of X1 and X2 (Künneth theorem, cf. [3]). For later use, we prove here a very particular case. This will serve also as an example of the notion of homotopy between complexes. ...
FROM INFINITESIMAL HARMONIC TRANSFORMATIONS TO RICCI
... 2. Examples of infinitesimal harmonic transformations In this section we will give four examples of infinitesimal harmonic transformations on Riemannian, nearly Kählerian and Kählerian manifolds. E x a m p l e 2.1. An infinitesimal isometric transformation on a Riemannian manifold is an infinitesim ...
... 2. Examples of infinitesimal harmonic transformations In this section we will give four examples of infinitesimal harmonic transformations on Riemannian, nearly Kählerian and Kählerian manifolds. E x a m p l e 2.1. An infinitesimal isometric transformation on a Riemannian manifold is an infinitesim ...
Tangents to Circles
... distance from you to a point of tangency is 16 feet. What is the radius of the silo? • First draw it. Tangent BC is perpendicular to radius AB at B, so ...
... distance from you to a point of tangency is 16 feet. What is the radius of the silo? • First draw it. Tangent BC is perpendicular to radius AB at B, so ...
Smooth manifolds - IME-USP
... needs not to be automatically Hausdorff, so one has to check that in each particular case and then the family {(Uα , ϕα )}α∈A is a smooth atlas for M . Further, instead of considering maximal smooth atlases, one can equivalently define a smooth structure on M to be an equivalence class of smooth atl ...
... needs not to be automatically Hausdorff, so one has to check that in each particular case and then the family {(Uα , ϕα )}α∈A is a smooth atlas for M . Further, instead of considering maximal smooth atlases, one can equivalently define a smooth structure on M to be an equivalence class of smooth atl ...
Math1330 objectives
... perform arithmetic on vectors and to solve application problems. Draw the components of a vector. Construct a visual representation of scalar multiplication, vector addition, and vector subtraction. Find the dot product of two vectors; find the angle between two vectors. Use the dot product to deter ...
... perform arithmetic on vectors and to solve application problems. Draw the components of a vector. Construct a visual representation of scalar multiplication, vector addition, and vector subtraction. Find the dot product of two vectors; find the angle between two vectors. Use the dot product to deter ...
26 - HKU
... holomorphic reduction of the tangent bundle to G. On an m-dimensional smooth manifold M , a Riemannian metric g on M gives a reduction of the structure group of the (real) tangent bundle from the general linear group GL(m, R) to the orthogonal group O(m). Riemannian geometry may be regarded as the g ...
... holomorphic reduction of the tangent bundle to G. On an m-dimensional smooth manifold M , a Riemannian metric g on M gives a reduction of the structure group of the (real) tangent bundle from the general linear group GL(m, R) to the orthogonal group O(m). Riemannian geometry may be regarded as the g ...
Unit 9 Vocabulary and Objectives File
... A line that contains a chord and continues through the circle to it’s exterior. A polygon whose vertices are on the circle and the sides of the polygon are made up of chords of the circle. The set of all points in space that are equal distance from a center point. Circles that lie in the same plane ...
... A line that contains a chord and continues through the circle to it’s exterior. A polygon whose vertices are on the circle and the sides of the polygon are made up of chords of the circle. The set of all points in space that are equal distance from a center point. Circles that lie in the same plane ...
Smooth Manifolds
... The simplest manifolds are the topological manifolds, which are topological spaces with certain properties that encode what we mean when we say that they “locally look like” Rn . Such spaces are studied intensively by topologists. However, many (perhaps most) important applications of manifolds invo ...
... The simplest manifolds are the topological manifolds, which are topological spaces with certain properties that encode what we mean when we say that they “locally look like” Rn . Such spaces are studied intensively by topologists. However, many (perhaps most) important applications of manifolds invo ...
Geometric and Solid Modeling Problems - Visgraf
... “It is necessary to have a better understanding of algorithmic modeling and its relation with geometric and solid modeling” ...
... “It is necessary to have a better understanding of algorithmic modeling and its relation with geometric and solid modeling” ...
Locally ringed spaces and manifolds
... In this lecture we shall define the category of Manifolds Mat giving a kdifferential atlas on a topological space X and the category of Manifolds MS h as a subcategory of the category of locally ringed spaces and then we shall prove that Mat and MS h are actually isomorphic. We shall reserve the sym ...
... In this lecture we shall define the category of Manifolds Mat giving a kdifferential atlas on a topological space X and the category of Manifolds MS h as a subcategory of the category of locally ringed spaces and then we shall prove that Mat and MS h are actually isomorphic. We shall reserve the sym ...
Reflections on manifolds
... We know that a group of orthogonal transformations in R2 consisting of at least one reflection is a dihedral group. Moreover, if the generator s, r meets at an angle of π/m then the reflection group is the coxeter group of order 2m with the presentation Dm = hs, r : s2 = r2 = (sr)m = 1i So, if we co ...
... We know that a group of orthogonal transformations in R2 consisting of at least one reflection is a dihedral group. Moreover, if the generator s, r meets at an angle of π/m then the reflection group is the coxeter group of order 2m with the presentation Dm = hs, r : s2 = r2 = (sr)m = 1i So, if we co ...
Lines that intersect Circles
... lie on a circle. Diameter: -a chord that contains the center -connects two points on the circle and passes through the center Secant: line that intersects a circle at two points ...
... lie on a circle. Diameter: -a chord that contains the center -connects two points on the circle and passes through the center Secant: line that intersects a circle at two points ...
Analytic functions and nonsingularity
... is an analytic map of affine analytic spaces. Example 1.8. A morphism of complex prevarieties gives an analytic map of the associated analytic spaces. Indeed, this follows from the fact that on an affine open cover, the morphism is given by tuples of polynomials, which are thus analytic. Abusing ter ...
... is an analytic map of affine analytic spaces. Example 1.8. A morphism of complex prevarieties gives an analytic map of the associated analytic spaces. Indeed, this follows from the fact that on an affine open cover, the morphism is given by tuples of polynomials, which are thus analytic. Abusing ter ...
After this lesson, you should be able to:
... a. Two circles are externally tangent if each of the tangent circles lies outside the other. b. Circle A and circle B are externally tangent. Name their point of tangency. c. What must be true about AB and CE ? d. CE is a common internal tangent because it lies between the circles. ...
... a. Two circles are externally tangent if each of the tangent circles lies outside the other. b. Circle A and circle B are externally tangent. Name their point of tangency. c. What must be true about AB and CE ? d. CE is a common internal tangent because it lies between the circles. ...
10.1 Use Properties of Tangents
... A line is tangent to a circle if and only if it’s ___________________________ to a _______________________ drawn to the point of tangency. ...
... A line is tangent to a circle if and only if it’s ___________________________ to a _______________________ drawn to the point of tangency. ...
Interactive Chalkboard
... plane of a circle that intersects the circle in exactly one point. Line j is a tangent. • A secant is a line that intersects a circle in two points. Line k is a secant. A secant contains a chord. ...
... plane of a circle that intersects the circle in exactly one point. Line j is a tangent. • A secant is a line that intersects a circle in two points. Line k is a secant. A secant contains a chord. ...
Differentiable manifold

In mathematics, a differentiable manifold is a type of manifold that is locally similar enough to a linear space to allow one to do calculus. Any manifold can be described by a collection of charts, also known as an atlas. One may then apply ideas from calculus while working within the individual charts, since each chart lies within a linear space to which the usual rules of calculus apply. If the charts are suitably compatible (namely, the transition from one chart to another is differentiable), then computations done in one chart are valid in any other differentiable chart.In formal terms, a differentiable manifold is a topological manifold with a globally defined differential structure. Any topological manifold can be given a differential structure locally by using the homeomorphisms in its atlas and the standard differential structure on a linear space. To induce a global differential structure on the local coordinate systems induced by the homeomorphisms, their composition on chart intersections in the atlas must be differentiable functions on the corresponding linear space. In other words, where the domains of charts overlap, the coordinates defined by each chart are required to be differentiable with respect to the coordinates defined by every chart in the atlas. The maps that relate the coordinates defined by the various charts to one another are called transition maps.Differentiability means different things in different contexts including: continuously differentiable, k times differentiable, smooth, and holomorphic. Furthermore, the ability to induce such a differential structure on an abstract space allows one to extend the definition of differentiability to spaces without global coordinate systems. A differential structure allows one to define the globally differentiable tangent space, differentiable functions, and differentiable tensor and vector fields. Differentiable manifolds are very important in physics. Special kinds of differentiable manifolds form the basis for physical theories such as classical mechanics, general relativity, and Yang–Mills theory. It is possible to develop a calculus for differentiable manifolds. This leads to such mathematical machinery as the exterior calculus. The study of calculus on differentiable manifolds is known as differential geometry.