circles theorems
... from the center of the circle to any point of the circle. The term radius is used to mean both the line segment and the length of the line segment. If A, B, and C are points of cirC cle O, then OA, OB, and OC are radii of the circle. Since the definition of a circle states that all points of the cir ...
... from the center of the circle to any point of the circle. The term radius is used to mean both the line segment and the length of the line segment. If A, B, and C are points of cirC cle O, then OA, OB, and OC are radii of the circle. Since the definition of a circle states that all points of the cir ...
Chapter 13 Answers
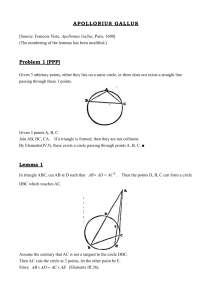
... 19. Isosceles nABC with vertex A is circumscribed about circle O, and D, E, and F are the points of tangency of AB, BC, and AC, respectively. By the isosceles triangle theorem, /DBE > /FCE. If two tangents are drawn to a circle from an external point, then the line segment from the center of the cir ...
... 19. Isosceles nABC with vertex A is circumscribed about circle O, and D, E, and F are the points of tangency of AB, BC, and AC, respectively. By the isosceles triangle theorem, /DBE > /FCE. If two tangents are drawn to a circle from an external point, then the line segment from the center of the cir ...
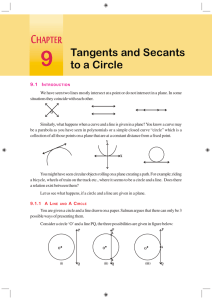
Tangents and Secants to a Circle
... have the radius of the circle and the angle between the tangents. We do not know the distance of the point from where the tangents are drawn to the circle and we do not know the length of the tangents either. We know only the angle between the tangents. Using this, we need to find out the distance o ...
... have the radius of the circle and the angle between the tangents. We do not know the distance of the point from where the tangents are drawn to the circle and we do not know the length of the tangents either. We know only the angle between the tangents. Using this, we need to find out the distance o ...
SSLC - MATHEMATICS CHAPTER 10 CIRCLES ENGLISH VERSION
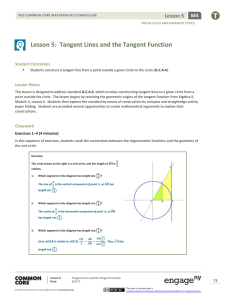
... The perpendicular to the radius at its non-centre end is the tangent to the circle. Observe that, in a circle angle between the radii and angle between the tangents drawn at their non-centre ends are supplementary. The perpendicular to the tangent at the point of contact passes through the centre of ...
... The perpendicular to the radius at its non-centre end is the tangent to the circle. Observe that, in a circle angle between the radii and angle between the tangents drawn at their non-centre ends are supplementary. The perpendicular to the tangent at the point of contact passes through the centre of ...
Chapter 13 - Haiku Learning
... 1. a. Draw three or four circles and one tangent for each circle. For each circle draw the radius to the point of tangency. b. Describe the relationship of each radius to the tangent. 2. a. Draw three or four circles and one radius for each circle. For each circle draw the line that is perpendicular ...
... 1. a. Draw three or four circles and one tangent for each circle. For each circle draw the radius to the point of tangency. b. Describe the relationship of each radius to the tangent. 2. a. Draw three or four circles and one radius for each circle. For each circle draw the line that is perpendicular ...
9-1 Basic Terms associated with Circles and Spheres
... 2) A regular polygon is inscribed in a circle so that all vertices of the quadrilateral intersect the circle. What happens to the regular polygon as the number of sides increases. ...
... 2) A regular polygon is inscribed in a circle so that all vertices of the quadrilateral intersect the circle. What happens to the regular polygon as the number of sides increases. ...
Basic Properties of Circle
... OT is a radius of the circle with centre O and AB is a straight line that intersects the circle at T. If AB is perpendicular to OT, then AB is a tangent to the circle at T. In other words, if AB OT, then AB is a tangent to the circle at T. (Reference: converse of tangent radius) Hence we can ded ...
... OT is a radius of the circle with centre O and AB is a straight line that intersects the circle at T. If AB is perpendicular to OT, then AB is a tangent to the circle at T. In other words, if AB OT, then AB is a tangent to the circle at T. (Reference: converse of tangent radius) Hence we can ded ...
Chapter 6 Notes: Circles
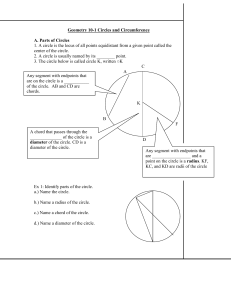
... the circle. Any line segment connecting the center and a point on the circle is called a radius of a circle. All radii of a circle are congruent. A diameter of a circle is a chord that contains the center of the circle. The length of the diameter is twice that of the radius. Congruent circles are tw ...
... the circle. Any line segment connecting the center and a point on the circle is called a radius of a circle. All radii of a circle are congruent. A diameter of a circle is a chord that contains the center of the circle. The length of the diameter is twice that of the radius. Congruent circles are tw ...
Note Sheets Chapter 6: Discovering and Proving Circle Properties
... • A segment that goes from the center to any point on the circle. • the distance from the center to any point on the circle. • All radii of a circle are equal. Diameter [of a circle] is • A chord that goes through the center of a circle. • Diameter is the longest chord in a circle. • the length of t ...
... • A segment that goes from the center to any point on the circle. • the distance from the center to any point on the circle. • All radii of a circle are equal. Diameter [of a circle] is • A chord that goes through the center of a circle. • Diameter is the longest chord in a circle. • the length of t ...
CIRCLES 10.1 Circles and Circumference CIRCLE
... 3. Then multiply the circumference of the circle by the ratio found in step 2. ...
... 3. Then multiply the circumference of the circle by the ratio found in step 2. ...
Mathematics Chapter: Tangents to Circles - JSUNIL tutorial
... Draw a line O'R parallel to PQ so that it makes a right angled triangle OO'R with OR = OP + PR = a + b units O'R = PQ = 7 units and OO' = d units By Pythagoras theorem, ...
... Draw a line O'R parallel to PQ so that it makes a right angled triangle OO'R with OR = OP + PR = a + b units O'R = PQ = 7 units and OO' = d units By Pythagoras theorem, ...
Date:10/01/2015 UNIT TEST Marks:55
... between their centers. 2) What are the angles in the Major segment? 3) What is the name of a straight line which intersects a circle at two distinct points? 4) The two circles are intersection, what is the maximum number of common tangents to be drawn? 5) What is the distance between the circles of ...
... between their centers. 2) What are the angles in the Major segment? 3) What is the name of a straight line which intersects a circle at two distinct points? 4) The two circles are intersection, what is the maximum number of common tangents to be drawn? 5) What is the distance between the circles of ...
CIRCLES 10.1 Circles and Circumference CIRCLE
... 3. Then multiply the circumference of the circle by the ratio found in step 2. ...
... 3. Then multiply the circumference of the circle by the ratio found in step 2. ...
definitions and theorems 6 - The Bronx High School of Science
... A circle is a set of points in a plane such that the points are equidistant froma fixed point called the center of the circle. A radius of a circle is a line segment from the center of the circle to any point of the circle. A central angle of a circle is n angle whose vertex is the center of t ...
... A circle is a set of points in a plane such that the points are equidistant froma fixed point called the center of the circle. A radius of a circle is a line segment from the center of the circle to any point of the circle. A central angle of a circle is n angle whose vertex is the center of t ...