Download ENSO nonlinearity in a warming climate

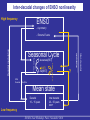
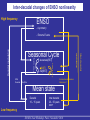
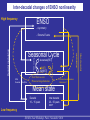
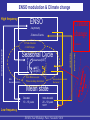
ENSO nonlinearity in a warming climate
Julien Boucharel
LEGOS / Univ. Toulouse, France
ewitte B., du Penhoat Y.
arel B.
eh S.-W.
Kug J.-S.
LEGOS / IRD, Toulouse, France
IMT / Univ. Toulouse, France
DEMS, Hanyang Univ., Ansan, South Korea
KORDI, Hanyang Univ., Ansan, South Korea
Why studying ENSO nonlinearity ?
LINEAR theories have provided an understanding of
the MAIN mechanisms leading to:
 the growth/decay of the initial SST perturbation
Bjerknes feedback
(Bjerknes, 1966)
 the oscillatory nature of ENSO
Delayed negative feedback of oceanic dynamic adjustment
(e.g. equatorial wave dynamics)
(Cane and Zebiak, 1985; Schopf and Suarez, 1988; Battisti
and Hirst, 1989 …)
ENSO Clivar Workshop, Paris, November 2010
Why studying ENSO nonlinearity ?
LINEAR theories have provided an understanding of
the MAIN mechanisms leading to:
 the growth/decay of the initial SST perturbation
Bjerknes feedback
(Bjerknes, 1966)
 the oscillatory nature of ENSO
Delayed negative feedback of oceanic dynamic adjustment
(e.g. equatorial wave dynamics)
(Cane and Zebiak, 1985; Schopf and Suarez, 1988; Battisti
and Hirst, 1989 …)
Regular and periodic oscillatory mode over a wide
range of parameters.
BUT …..
ENSO Clivar Workshop, Paris, November 2010
SSTA [°C]
Niño3 SST anomalies from Kaplan reconstruction (Kaplan et al., 1998).
Time [Year]
Strongly irregular behaviour of ENSO related timeseries
ENSO Clivar Workshop, Paris, November 2010
SSTA [°C]
Niño3 SST anomalies from Kaplan reconstruction (Kaplan et al., 1998).
12-years running mean
Time [Year]
Slowly varying mean state
Inter-decadal variability
ENSO Clivar Workshop, Paris, November 2010
Niño3 SST anomalies from Kaplan reconstruction (Kaplan et al., 1998).
SSTA [°C]
1976 Warm shift
1998 Cold shift
1903 Cold shift
Time [Year]
Inter-decadal variability reflected by the presence of abrupt transitions
(Climate shifts)
Bivariate test for the detection of a systematic change in mean (shift)
Maronna and Yohai (1978), Potter (1981), Boucharel et al. (2009)
ENSO Clivar Workshop, Paris, November 2010
Niño3 SST anomalies from Kaplan reconstruction (Kaplan et al., 1998).
Positive asymmetry
Pseudo symmetry
Skewness > 0
Skewness ~ 0
Positive
asymmetry
Pseudo
symmetry
Skewness > 0
Skewness ~ 0
SSTA [°C]
1 n
skewness  m3   ( xk  x) 3
n k 1
Time [Year]
Homogenous periods in terms of ENSO characteristics:
- Variability
- Asymmetry
- Frequency
- Predictability …
ENSO Clivar Workshop, Paris, November 2010
SSTA [°C]
Niño3 SST anomalies from Kaplan reconstruction (Kaplan et al., 1998).
Time [Year]
Presence of "anomalous" Extreme Events
Complexity of ENSO system on a wide range of timescales
ENSO Clivar Workshop, Paris, November 2010
Why studying ENSO nonlinearity ?
(Inter-)decadal changes of ENSO characteristics mirror (inter-)decadal
changes of nonlinearity (as measured by ENSO asymmetry).
An and Wang, 2000; Wu and Hsieh, 2003; An, 2004; Ye and Hsieh,
2006….
Dynamical linkage between these changes (An, 2009)
Nonlinear processes are part of the ENSO system and
may be involved in ENSO low-frequency modulation
ENSO Clivar Workshop, Paris, November 2010
Outline:
1. Measuring the nonlinearity of ENSO
2. Interactive feedback between ENSO irregularity and low-frequency
variability
3. ENSO statistics in a warming climate
4. Conclusions, perspectives
ENSO Clivar Workshop, Paris, November 2010
Outline:
1. Measuring the nonlinearity of ENSO
2. Interactive feedback between ENSO irregularity and low-frequency
variability
3. ENSO statistics in a warming climate
4. Conclusions, perspectives
ENSO Clivar Workshop, Paris, November 2010
Quantifying ENSO nonlinearity
Statistical measure
Number of occurences
Summary of ENSO statistical properties: Probability Density Function
Gaussian curve
corresponding to the best
sampled PDF fit.
[°C]
Smoothed histogram of monthly SST anomalies (1870-2009) averaged in Niño3
ENSO Clivar Workshop, Paris, November 2010
Quantifying ENSO nonlinearity
Statistical measure
Summary of ENSO statistical properties: Probability Density Function
Number of occurences
Presence of
Extreme Events…
[°C]
Smoothed histogram of monthly SST anomalies (1870-2009) averaged in Niño3
ENSO Clivar Workshop, Paris, November 2010
Quantifying ENSO nonlinearity
Statistical measure
Summary of ENSO statistical properties: Probability Density Function
Number of occurences
Presence of
Extreme Events…
and a strong
positive
asymmetry
[°C]
Smoothed histogram of monthly SST anomalies (1870-2009) averaged in Niño3
ENSO Clivar Workshop, Paris, November 2010
Quantifying ENSO nonlinearity
Statistical measure
Summary of ENSO statistical properties: Probability Density Function
Contraction of the
PDF near 0
Number of occurences
Presence of
Extreme Events…
and a strong
positive
asymmetry
[°C]
Smoothed histogram of monthly SST anomalies (1870-2009) averaged in Niño3
ENSO Clivar Workshop, Paris, November 2010
Quantifying ENSO nonlinearity
Hypothesis:
- The "distorsion" of the PDF of tropical Pacific climate variables is a signature
of the presence of nonlinearity in the ENSO system.
 Quantifying this distorsion can provide insights on an integrated
level of ENSO nonlinearity
Up to now, only ENSO asymmetry (skewness) has been considered to
document the tropical pacific nonlinearity
(Burgers and Stephenson, 1999; An and Jin, 2004)
But other ENSO statistical peculiarities have to be taken into account
 Need to propose a quantification of the presence of EE, the
leptokurtic deformation and the asymmetry of ENSO PDF
 Higher order statistics
ENSO Clivar Workshop, Paris, November 2010
Quantifying ENSO nonlinearity
 ENSO statistical specificities prompt us to consider heavy-tails laws family:
ENSO Clivar Workshop, Paris, November 2010
Quantifying ENSO nonlinearity
 ENSO statistical specificities prompt us to consider heavy-tails laws family:
The a-stable law, an example of the
wide heavy-tails laws family:
Lévy (1924); Mandelbrot (1960, 1963).
Benoît Mandelbrot (1924-2010)
ENSO Clivar Workshop, Paris, November 2010
Quantifying ENSO nonlinearity
 ENSO statistical specificities prompt us to consider heavy-tails laws family:
The a-stable law, an example of the
wide heavy-tails laws family:
Lévy (1924); Mandelbrot (1960, 1963).
Benoît Mandelbrot (1924-2010)
Characteristic
function:

 (t )  E[exp itX ]  exp  g a t 1  ib sign (t )w(t , a )  id t
def
a
4 parameters govern stable distributions
a, b, g and d
ENSO Clivar Workshop, Paris, November 2010

Quantifying ENSO nonlinearity
 ENSO statistical specificities prompt us to consider heavy-tails laws family:
The a-stable law, an example of the
wide heavy-tails laws family:
Lévy (1924); Mandelbrot (1960, 1963).
Benoît Mandelbrot (1924-2010)
Characteristic
function:

 (t )  E[exp itX ]  exp  g a t 1  ib sign (t )w(t , a )  id t
def
a
4 parameters govern stable distributions
a, b, g and d
ENSO Clivar Workshop, Paris, November 2010

Quantifying ENSO nonlinearity
 a-stable laws, examples
Dependance on a
d=0
b =0
g =1
ENSO Clivar Workshop, Paris, November 2010
Quantifying ENSO nonlinearity
 a-stable laws, examples
Dependance on a
d=0
b =0
g =1
 a controls the leptokurtic deformation of the PDF
a associated with the kurtosis (≥ 4th-order statistical moment)
ENSO Clivar Workshop, Paris, November 2010
Quantifying ENSO nonlinearity
 a-stable laws, examples
Dependance on b
Dependance on a
b=0
b = 0.5
b = 0.8
b=1
d=0
b =0
g =1
 a controls the leptokurtic deformation of the PDF
a associated with the kurtosis (≥ 4th-order statistical moment)
b associated with the skewness (= 3rd-order statistical moment)
ENSO Clivar Workshop, Paris, November 2010
a = 1.2
d =0
g =1
Quantifying ENSO nonlinearity
 a-stable laws, examples
Dependance on b
Dependance on a
b=0
b = 0.5
b = 0.8
b=1
d=0
b =0
g =1
 a controls the leptokurtic deformation of the PDF
a associated with the kurtosis (≥ 4th-order statistical moment)
b associated with the skewness (= 3rd-order statistical moment)
ENSO Clivar Workshop, Paris, November 2010
a = 1.2
d =0
g =1
a=2b=0
Gaussian distribution
Quantifying ENSO nonlinearity
 Estimation of a-stable parameters
Koutrouvelis (1980):
Regression method using the sample characteristic function:

 (t )  E[exp itX ]  exp  g a t 1  ib sign (t )w(t , a )  id t
def
a

Rigorous statistical framework to quantify
equivalent of high order statistical moments
of ENSO timeseries
Metrics of nonlinearity
ENSO Clivar Workshop, Paris, November 2010
Quantifying ENSO nonlinearity
 Estimation of a-stable parameters
a
b
a-stable parameters inferred from Kaplan reconstruction SST
anomalies on the 1870-2009 period.
ENSO Clivar Workshop, Paris, November 2010
Quantifying ENSO nonlinearity
 Estimation of a-stable parameters
a
Gaussian features
During the last 130 years,
most of the tropical Pacific
exhibit a-stable properties.
Coherent with other
reconstructions (HadSST,
ERSST)
b
a-stable parameters inferred from Kaplan reconstruction SST
anomalies on the 1870-2009 period.
ENSO Clivar Workshop, Paris, November 2010
Quantifying ENSO nonlinearity
 Estimation of a-stable parameters
a
Gaussian features
During the last 130 years,
most of the tropical Pacific
exhibit a-stable properties.
Coherent with other
reconstructions (HadSST,
ERSST)
b
Particularly the Warm Pool
and the Cold Tongue
regions
a-stable parameters inferred from Kaplan reconstruction SST
anomalies on the 1870-2009 period.
ENSO Clivar Workshop, Paris, November 2010
Quantifying ENSO nonlinearity
 Estimation of a-stable parameters
a
Gaussian features
During the last 130 years,
most of the tropical Pacific
exhibit a-stable properties.
Coherent with other
reconstructions (HadSST,
ERSST)
b
Particularly the Warm Pool
and the Cold Tongue
regions
The asymmetry map
exhibits a zonal see-saw
pattern
a-stable parameters inferred from Kaplan reconstruction SST
anomalies on the 1870-2009 period.
ENSO Clivar Workshop, Paris, November 2010
Outline:
1. Measuring the nonlinearity of ENSO
2. Interactive feedback between ENSO irregularity and lowfrequency variability
3. ENSO statistics in a warming climate
4. Conclusions, perspectives
ENSO Clivar Workshop, Paris, November 2010
Inter-decadal changes of ENSO nonlinearity
SSTA [°C]
Estimation of a and b on each period
Time [Year]
ENSO Clivar Workshop, Paris, November 2010
Inter-decadal changes of ENSO nonlinearity
 Estimation of a-stable law main parameters (Boucharel et al., 2009):
a
b
 Distinct nonlinear
1870-1903:
behaviours according
to the tropical mean
state
1903-1976:
1976-1998:
1998-2009:
ENSO Clivar Workshop, Paris, November 2010
Inter-decadal changes of ENSO nonlinearity
 Estimation of a-stable law main parameters (Boucharel et al., 2009):
a
b
 Distinct nonlinear
1870-1903:
behaviours according
to the tropical mean
state
1903-1976:
1976-1998:
1998-2009:
ENSO Clivar Workshop, Paris, November 2010
 Alternation of
periods favouring
Extreme Events
triggering in the Cold
Tongue with other in
the Warm Pool
Inter-decadal changes of ENSO nonlinearity
 Estimation of a-stable law main parameters (Boucharel et al., 2009):
a
b
 Distinct nonlinear
1870-1903:
behaviours according
to the tropical mean
state
1976-1998:
 Alternation of
periods favouring
Extreme Events
triggering in the Cold
Tongue with other in
the Warm Pool
1998-2009:
 Low frequency
modulation of the
nonlinearity imprint in
the tropical Pacific
1903-1976:
ENSO Clivar Workshop, Paris, November 2010
Inter-decadal changes of ENSO nonlinearity
High frequency
ENSO
Irregularity
- Asymmetry
- Extreme Events
Inter-decadal
Modulation
Mean state
Low frequency
Inter-decadal
20 – 50 years
INTER-SHIFT periods
ENSO Clivar Workshop, Paris, November 2010
Inter-decadal changes of ENSO nonlinearity
High frequency
ENSO
Irregularity
- Asymmetry
- Extreme Events
Mean state
Low frequency
Inter-decadal
20 – 50 years
INTER-SHIFT periods
ENSO Clivar Workshop, Paris, November 2010
Inter-decadal
Modulation
?
2-ways feedback ?
Is the ENSO irregularity associated
with Extreme Events able to act
back on the tropical Pacific mean
state?
Inter-decadal changes of ENSO nonlinearity
An and Choi (2009)
Decadal changes in the
seasonality
of the ENSO asymmetry
may influence the decadal
changes in
the amplitude of the annual
and semi-annual cycles,
and therefore the tropical
Pacific decadal mean
state.
Fig. 1. Annual cycle of variance (dashed line; scales in the right yaxis) and skewness (solid line; scales in the left y-axis) of Niño-3
index obtained from ERSST data averaged over 1880 to 2007.
ENSO Clivar Workshop, Paris, November 2010
Inter-decadal changes of ENSO nonlinearity
An and Choi (2009)
Fig. 1. Annual cycle of variance (dashed line; scales in the right yaxis) and skewness (solid line; scales in the left y-axis) of Niño-3
index obtained from ERSST data averaged over 1880 to 2007.
Decadal changes in the
seasonality
of the ENSO asymmetry
may influence the decadal
changes in
the amplitude of the annual
and semi-annual cycles,
and therefore the tropical
Pacific decadal mean
state.
This is
because the seasondependent nonlinear
rectification can
modify the annual and
semi-annual cycles.
ENSO Clivar Workshop, Paris, November 2010
Inter-decadal changes of ENSO nonlinearity
SSTA [°C]
season-dependant
An and Choi (2009)
Dewitte et al. (2007)
Timmermann et al. (2003)
Time [year]
ENSO Clivar Workshop, Paris, November 2010
Inter-decadal changes of ENSO nonlinearity
High frequency
ENSO
- Asymmetry
Phase locking
- skewness[SST]
- Var[SST]
NDH
Residual Niño/Niña
Mean state
Decadal
10 – 15 years
Inter-decadal
20 – 50 years
SHIFT
Low frequency
ENSO Clivar Workshop, Paris, November 2010
Inter-decadal
Seasonal Cycle
modulation
Decadal modulation
- Extreme Events
Inter-decadal changes of ENSO nonlinearity
High frequency
ENSO
- Asymmetry
- skewness[SST]
- a[SST]
- Var[SST]
NDH
Residual Niño/Niña
Phase locking ???
Phase locking
modulation
Seasonal Cycle
Mean state
Decadal
10 – 15 years
Inter-decadal
20 – 50 years
SHIFT
Low frequency
ENSO Clivar Workshop, Paris, November 2010
?
Inter-decadal
Decadal modulation
- Extreme Events
Inter-decadal changes of ENSO nonlinearity
150°E
190°E
NINO4W
210°E
270°E
5°N
NINO3
5°S
[2 – a]NINO3
[2 – a]NINO4W
NINO4W
estimation of a parameter on a 15-years running window
ENSO Clivar Workshop, Paris, November 2010
 Inter-decadal
variability of
nonlinearity as
measured by [2-a
Inter-decadal changes of ENSO nonlinearity
150°E
190°E
NINO4W
210°E
270°E
5°N
NINO3
5°S
[2 – a]NINO3
[2 – a]NINO4W
NINO4W
estimation of a parameter on a 15-years running window
ENSO Clivar Workshop, Paris, November 2010
 Inter-decadal
variability of
nonlinearity as
measured by [2-a
 Eastern and
Western Tropical
Pacific out of phase
Inter-decadal changes of ENSO nonlinearity
150°E
190°E
NINO4W
210°E
270°E
5°N
NINO3
5°S
[2 – a]NINO3
[2 – a]NINO4W
NINO4W
estimation of a parameter on a 15-years running window
ENSO Clivar Workshop, Paris, November 2010
 Inter-decadal
variability of
nonlinearity as
measured by [2-a
 Eastern and
Western Tropical
Pacific out of phase
 Do these long-term
variations have the
ability to influence
seasonal SST
variations and to
rectify into the interdecadal mean state ?
Inter-decadal changes of ENSO nonlinearity
150°E
190°E
NINO4W
210°E
270°E
5°N
NINO3
5°S
[2 – a]NINO3
[2 – a]NINO4W
NINO4W
estimation of a parameter on a 15-years running window
ENSO Clivar Workshop, Paris, November 2010
 Inter-decadal
variability of
nonlinearity as
measured by [2-a
 Eastern and
Western Tropical
Pacific out of phase
 Do these long-term
variations have the
ability to influence
seasonal SST
variations and to
rectify into the interdecadal mean state ?
Inter-decadal changes of ENSO nonlinearity
 Opposite behaviour between two consecutive
inter-shifts periods
Mean[SST]
1903-1925
1925-1940
Var[SST]
NINO3
a[SST]
NINO4
West
ENSO Clivar Workshop, Paris, November 2010
Inter-decadal changes of ENSO nonlinearity
 Opposite behaviour between two consecutive
inter-shifts periods
 Inter-decadal changes in amplitude and phase
of mean seasonal cycle
Mean[SST]
1903-1925
1925-1940
Phase locking
Var[SST]
NINO3
Anti Phase locking
a[SST]
Phase locking
Anti Phase locking
ENSO Clivar Workshop, Paris, November 2010
NINO4
West
Inter-decadal changes of ENSO nonlinearity
 Opposite behaviour between two consecutive
inter-shifts periods
 Inter-decadal changes in amplitude and phase
of mean seasonal cycle
Extreme Events residual can be rectified into the
inter-decadal tropical Pacific mean state
Mean[SST]
1903-1925
1925-1940
Phase locking
Var[SST]
NINO3
Anti Phase locking
a[SST]
Phase locking
Anti Phase locking
ENSO Clivar Workshop, Paris, November 2010
NINO4
West
Inter-decadal changes of ENSO nonlinearity
SSTA [°C]
Time [year]
ENSO Clivar Workshop, Paris, November 2010
Inter-decadal changes of ENSO nonlinearity
SSTA [°C]
=
+
Time [year]
ENSO low-frequency modulation
due to its own irregularity
ENSO Clivar Workshop, Paris, November 2010
Inter-decadal changes of ENSO nonlinearity
High frequency
ENSO
- Asymmetry
- skewness[SST]
- a[SST]
- Var[SST]
Phase locking
Phase locking
modulation
Seasonal Cycle
NDH
Residual Niño/Niña
Extreme Events Residual
Mechanism ?
Mean state
Decadal
10 – 15 years
Inter-decadal
20 – 50 years
SHIFT
Low frequency
ENSO Clivar Workshop, Paris, November 2010
Inter-decadal
Decadal modulation
- Extreme Events
Inter-decadal changes of ENSO nonlinearity
High frequency
ENSO
- Asymmetry
Phase locking
- skewness[SST]
- a[SST]
- Var[SST]
East-West see-saw
Phase-locking alternation
Phase locking
NDH
Residual Niño/Niña
modulation
Seasonal Cycle
Extreme Events Residual
Mechanism ?
Mean state
Decadal
10 – 15 years
Inter-decadal
20 – 50 years
SHIFT
Low frequency
ENSO Clivar Workshop, Paris, November 2010
Inter-decadal
Decadal modulation
- Extreme Events
Outline:
1. Measuring the nonlinearity of ENSO
2. Interactive feedback between ENSO irregularity and low-frequency
variability
3. ENSO statistics in a warming climate
4. Conclusions, perspectives
ENSO Clivar Workshop, Paris, November 2010
ENSO statistics in a warming climate
 IPCC database
Models selection according to recent multimodel studies
Model Name
Length of PICTRL run
Length of 2xCO2 run
Length of 4xCO2 run
1
BCCR-BCM2.0
250
100
-
2
CCCMA-CGCM3.1-t47
500
220
290
3
CSIRO-MK3.5 run1
180
80
-
4
CSIRO-MK3.5 run2
100
-
-
5
GFDL-CM2.0
200
280
300
6
GFDL-CM2.1
100
200
200
7
GISS-MODEL-E-H
280
220
-
8
INM-CM3.0
330
220
290
9
MIROC3.2-HIRES
100
220
-
10
MIROC3.2-MEDRES
run1
500
220
290
11
MIROC3.2-MEDRES
run2
-
70
140
12
MIROC3.2-MEDRES
run3
-
70
140
13
MRI-CGCM2.3.2A
300
220
290
14
UKMO-HadCM3 (run1)
341
220
220
ENSO Clivar Workshop, Paris, November 2010
ENSO statistics in a warming climate
 IPCC database
Models selection according to recent multimodel studies and 3 scenarios
Model Name
Length of PICTRL run
Length of 2xCO2 run
Length of 4xCO2 run
1
BCCR-BCM2.0
250
100
-
2
CCCMA-CGCM3.1-t47
500
220
290
3
CSIRO-MK3.5 run1
180
80
-
4
CSIRO-MK3.5 run2
100
-
-
5
GFDL-CM2.0
200
280
300
6
GFDL-CM2.1
100
200
200
7
GISS-MODEL-E-H
280
220
-
8
INM-CM3.0
330
220
290
9
MIROC3.2-HIRES
100
220
-
10
MIROC3.2-MEDRES
run1
500
220
290
11
MIROC3.2-MEDRES
run2
-
70
140
12
MIROC3.2-MEDRES
run3
-
70
140
13
MRI-CGCM2.3.2A
300
220
290
14
UKMO-HadCM3 (run1)
341
220
220
ENSO Clivar Workshop, Paris, November 2010
ENSO statistics in a warming climate
 a-stable parameters:
Da  a2xCO2 – aPICTRL
Db  b2xCO2 – bPICTRL
MultiModels
Mean
More nonlinear
2xCO2 – PICTRL:
More linear
More negative asym
More positive asym
Boucharel et al. (2010), in rev.
- Patterns of b indicate more drastic changes over Niño4 region.
ENSO Clivar Workshop, Paris, November 2010
ENSO statistics in a warming climate
 a-stable parameters:
Da  a2xCO2 – aPICTRL
Db  b2xCO2 – bPICTRL
MultiModels
Mean
More nonlinear
More linear
2xCO2 – PICTRL:
More negative asym
More positive asym
Boucharel et al. (2010), in rev.
- Patterns of b indicate more drastic changes over Niño4 region.
- Zonal tripole pattern of a
ENSO Clivar Workshop, Paris, November 2010
ENSO statistics in a warming climate
 a-stable parameters:
Da  a2xCO2 – aPICTRL
Db  b2xCO2 – bPICTRL
MultiModels
Mean
More nonlinear
More linear
2xCO2 – PICTRL:
More negative asym
More positive asym
Boucharel et al. (2010), in rev.
- Patterns of b indicate more drastic changes over Niño4 region.
- Zonal tripole pattern of a
 Intensification of Extreme El Niño events and nonlinearity over the western
Pacific (« Modoki »)
 Decrease of the traditional Cold Tongue El Niño.
ENSO Clivar Workshop, Paris, November 2010
ENSO statistics in a warming climate
 a-stable parameters:
More nonlinear
More linear
More negative asym
Da  a4xCO2 – aPICTRL
More positive asym
Db  b4xCO2 – bPICTRL
MultiModels
Mean
4xCO2 – PICTRL:
ENSO Clivar Workshop, Paris, November 2010
ENSO statistics in a warming climate
 a-stable parameters:
More nonlinear
More linear
More negative asym
Da  a4xCO2 – aPICTRL
More positive asym
Db  b4xCO2 – bPICTRL
MultiModels
Mean
4xCO2 – PICTRL:
-
-
Same tendency than for 2xCO2 – PICTRL. Patterns of change not altered
Treshold effect of climate change impact on the mean state
ENSO Clivar Workshop, Paris, November 2010
ENSO statistics in a warming climate
 Is it an artefact of one particular model ?
ENSO Clivar Workshop, Paris, November 2010
ENSO statistics in a warming climate
 Is it an artefact of one particular model ?
b
Niño4W
A
Niño4W
'
a trip
 a'
A
 a'
Niño3
Niño4W
Niño3
 a'
Niño4W
 2 [ a
A
 a
Niño3
 a
Niño4W
]
ENSO Clivar Workshop, Paris, November 2010
ENSO statistics in a warming climate
Ensemble
mean
 Wide range of behaviours in terms of nonlinearity
ENSO Clivar Workshop, Paris, November 2010
ENSO statistics in a warming climate
Ensemble
mean
 Wide range of behaviours in terms of nonlinearity
 But 10/14 models exhibit a decrease in a'trip with 70 % of them being confident at 95%
ENSO Clivar Workshop, Paris, November 2010
ENSO statistics in a warming climate
Ensemble
Mean for
NINO4W
 Wide range of behaviours in terms of nonlinearity
 But 10/14 models exhibit a decrease in a'trip with 70 % of them being confident at 95%
 Dominated by changes over the western tropical Pacific
ENSO Clivar Workshop, Paris, November 2010
ENSO statistics in a warming climate
 Confirmed by asymmetry changes
 Decrease towards a strong negative asymmetry.
 Reduction of asymmetry in the Cold Tongue (not shown).
ENSO Clivar Workshop, Paris, November 2010
ENSO statistics in a warming climate
Mean[SST]
Var[SST]
 Beyond interdecadal variability,
dominant phaselocking in the
Eastern Pacific in
20th century and
pre-industrial climate
a[SST]
ENSO Clivar Workshop, Paris, November 2010
ENSO statistics in a warming climate
Mean[SST]
Var[SST]
Var[SST]
 Beyond interdecadal variability,
dominant phaselocking in the
Eastern Pacific in
20th century and
pre-industrial climate
a[SST]
a[SST]
 In a warming
climate, dominant
phase-locking in the
Western Pacific
ENSO Clivar Workshop, Paris, November 2010
ENSO statistics in a warming climate
Mean[SST]
Var[SST]
Var[SST]
 Beyond interdecadal variability,
dominant phaselocking in the
Eastern Pacific in
20th century and
pre-industrial climate
a[SST]
a[SST]
 In a warming
climate, dominant
phase-locking in the
Western Pacific
Change in
dynamic attractor,
Bifurcation ?
ENSO Clivar Workshop, Paris, November 2010
Outline:
1. Measuring the nonlinearity of ENSO
2. Interactive feedback between ENSO irregularity and low-frequency
variability
3. ENSO statistics in a warming climate
4. Conclusions, perspectives
ENSO Clivar Workshop, Paris, November 2010
Conclusions
 a-stable laws allow defining relevant and mathematically defined metrics of highstatistical moments and therefore nonlinearity
 High Statistical moments = important indicators of human-induced climate change
(Timmermann, 1999).
ENSO Clivar Workshop, Paris, November 2010
Conclusions
 a-stable laws allow defining relevant and mathematically defined metrics of highstatistical moments and therefore nonlinearity
 High Statistical moments = important indicators of human-induced climate change
(Timmermann, 1999).
 Tropical Pacific system nonlinear by nature (Jin et al., 1994; Tziperman et al., 1994)
 Nonlinearity associated with EE are involved in low-frequency modulation and may be
responsible for abrupt transitions of tropical Pacific mean state (climate shifts).
 Evidence of a significant change in nonlinearity patterns under greenhouse warming
Changes not so sensitive between 2xCO2 and 4xCO2  Threshold / bifurcation
crossed ?
ENSO Clivar Workshop, Paris, November 2010
Conclusions
 a-stable laws allow defining relevant and mathematically defined metrics of highstatistical moments and therefore nonlinearity
 High Statistical moments = important indicators of human-induced climate change
(Timmermann, 1999).
 Tropical Pacific system nonlinear by nature (Jin et al., 1994; Tziperman et al., 1994)
 Nonlinearity associated with EE are involved in low-frequency modulation and may be
responsible for abrupt transitions of tropical Pacific mean state (climate shifts).
 Evidence of a significant change in nonlinearity patterns under greenhouse warming
Changes not so sensitive between 2xCO2 and 4xCO2  Threshold / bifurcation
crossed ?
 Apply this method on the new generations of CGCMs (CMIP5) even in PMIP (longer
timeseries)
 Identify the nonlinear processes associated with these changes (NDH, intra seasonal
variability, TIW …?)
ENSO Clivar Workshop, Paris, November 2010
ENSO modulation & Climate change
High frequency
ENSO
Climate
change
- Asymmetry
- Extreme Events
Treshold
Phase locking
- skewness[SST]
- a[SST]
- Var[SST]
East-West see-saw
Phase-locking alternation
Phase locking
NDH
Residual Niño/Niña
modulation
Seasonal Cycle
Extreme Events Residual
Mechanism ?
Mean state
Decadal
10 – 15 years
Inter-decadal
20 – 50 years
SHIFT
Low frequency
ENSO Clivar Workshop, Paris, November 2010
Inter-decadal
Decadal modulation
El Niño Modoki
– Cold Tongue
THANK YOU
ENSO Clivar Workshop, Paris, November 2010